最小二乘拟合

Posted 2021-11-24 focus-z

http://www.cnblogs.com/cv-pr/p/4741262.html
https://blog.csdn.net/lotus___/article/details/20546259

 

二. 最小二乘法

   我们以最简单的一元线性模型来解释最小二乘法。什么是一元线性模型呢？ 监督学习中，如果预测的变量是离散的，我们称其为分类（如决策树，支持向量机等），如果预测的变量是连续的，我们称其为回归。回归分析中，如果只包括一个自变量和一个因变量，且二者的关系可用一条直线近似表示，这种回归分析称为一元线性回归分析。如果回归分析中包括两个或两个以上的自变量，且因变量和自变量之间是线性关系，则称为多元线性回归分析。对于二维空间线性是一条直线；对于三维空间线性是一个平面，对于多维空间线性是一个超平面...

   对于一元线性回归模型, 假设从总体中获取了n组观察值（X1，Y1），（X2，Y2）， …，（Xn，Yn）。对于平面中的这n个点，可以使用无数条曲线来拟合。要求样本回归函数尽可能好地拟合这组值。综合起来看，这条直线处于样本数据的中心位置最合理。 选择最佳拟合曲线的标准可以确定为：使总的拟合误差（即总残差）达到最小。有以下三个标准可以选择：

        （1）用“残差和最小”确定直线位置是一个途径。但很快发现计算“残差和”存在相互抵消的问题。
        （2）用“残差绝对值和最小”确定直线位置也是一个途径。但绝对值的计算比较麻烦。
        （3）最小二乘法的原则是以“残差平方和最小”确定直线位置。用最小二乘法除了计算比较方便外，得到的估计量还具有优良特性。这种方法对异常值非常敏感。

　 最常用的是普通最小二乘法（ Ordinary  Least Square，OLS）：所选择的回归模型应该使所有观察值的残差平方和达到最小。（Q为残差平方和）- 即采用平方损失函数。

 　样本回归模型：

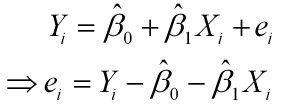                                     其中e_i为样本（X_i, Y_i）的误差

   平方损失函数：

                      

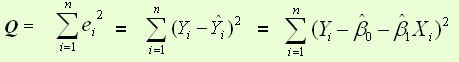
   则通过Q最小确定这条直线，即确定，以为变量，把它们看作是Q的函数，就变成了一个求极值的问题，可以通过求导数得到。求Q对两个待估参数的偏导数：

                       

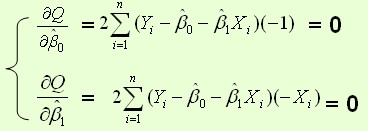
    根据数学知识我们知道，函数的极值点为偏导为0的点。

    解得：

                   

 

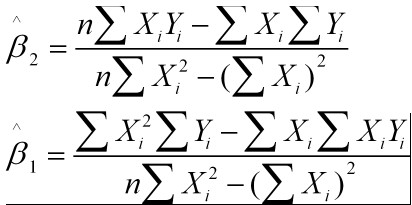
这就是最小二乘法的解法，就是求得平方损失函数的极值点。

 

三. C++实现代码

 1 /*
 2 最小二乘法C++实现
 3 参数1为输入文件
 4 输入 ： x
 5 输出： 预测的y  
 6 */
 7 #include<iostream>
 8 #include<fstream>
 9 #include<vector>
10 using namespace std;
11 
12 class LeastSquare{
13     double a, b;
14 public:
15     LeastSquare(const vector<double>& x, const vector<double>& y)
16     {
17         double t1=0, t2=0, t3=0, t4=0;
18         for(int i=0; i<x.size(); ++i)
19         {
20             t1 += x[i]*x[i];
21             t2 += x[i];
22             t3 += x[i]*y[i];
23             t4 += y[i];
24         }
25         a = (t3*x.size() - t2*t4) / (t1*x.size() - t2*t2);  // 求得β1 
26         b = (t1*t4 - t2*t3) / (t1*x.size() - t2*t2);        // 求得β2
27     }
28 
29     double getY(const double x) const
30     {
31         return a*x + b;
32     }
33 
34     void print() const
35     {
36         cout<<"y = "<<a<<"x + "<<b<<"\\n";
37     }
38 
39 };
40 
41 int main(int argc, char *argv[])
42 {
43     if(argc != 2)
44     {
45         cout<<"Usage: DataFile.txt"<<endl;
46         return -1;
47     }
48     else
49     {
50         vector<double> x;
51         ifstream in(argv[1]);
52         for(double d; in>>d; )
53             x.push_back(d);
54         int sz = x.size();
55         vector<double> y(x.begin()+sz/2, x.end());
56         x.resize(sz/2);
57         LeastSquare ls(x, y);
58         ls.print();
59         
60         cout<<"Input x:\\n";
61         double x0;
62         while(cin>>x0)
63         {
64             cout<<"y = "<<ls.getY(x0)<<endl;
65             cout<<"Input x:\\n";
66         }
67     }
68 }