凸优化4 凸函数
Posted shenhaojing
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了凸优化4 凸函数相关的知识,希望对你有一定的参考价值。
引言
本文先介绍凸函数的4种定义方式,然后介绍一些凸函数。
凸函数的第一个定义
\\(f: R^n \\rightarrow R\\)为凸函数,等价于:\\(dom f\\)为凸,且
\\[\\forall x,y \\in dom f, 0 \\leq \\theta \\leq 1\\]
有
\\[f(\\theta x + (1-\\theta)y) \\leq \\theta f(x) + (1 - \\theta)f(y)\\]
凸函数的第二个定义(高维情况下用的比较多)
若\\(f:R^n \\rightarrow R\\)为凸,等价于:
\\(dom f\\)为凸,\\(\\forall x \\in dom f, \\forall v\\),
\\[g(t) = f(x + tv)\\]
为凸函数,\\(dom g=\\t|x+tv \\in dom f\\\\)
凸函数的第三个定义:一阶条件
设\\(f: R^n \\rightarrow R\\)可微,即梯度\\(\\bigtriangledown f\\)在\\(dom f\\)上均存在,则\\(f\\)为凸函数等价于:
\\(dom f\\)为凸。
\\(f(y) \\geq f(x) + \\bigtriangledown f^T(x)(y-x), \\forall x,y \\in dom f\\)
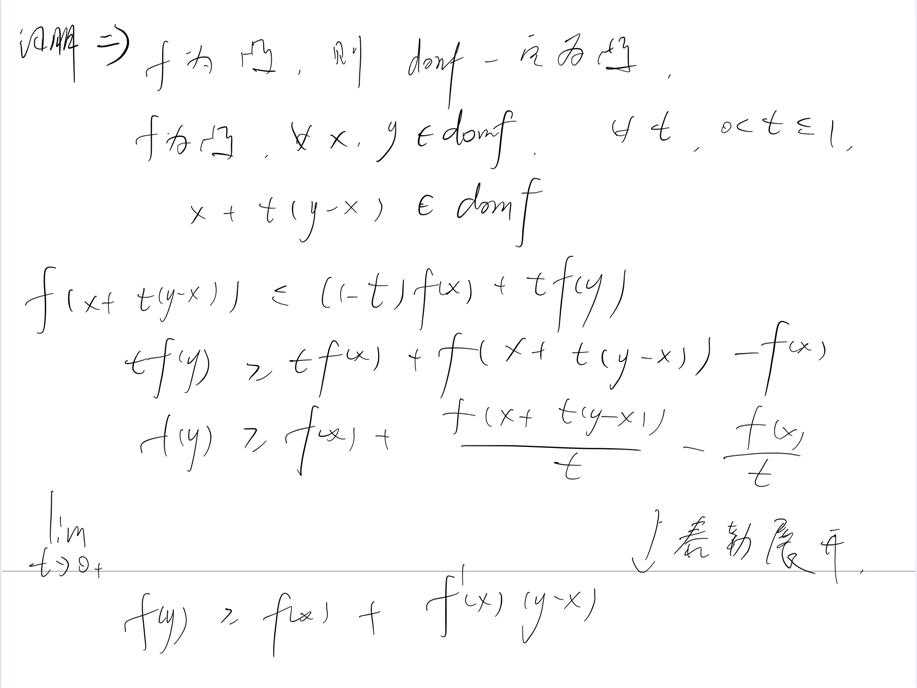
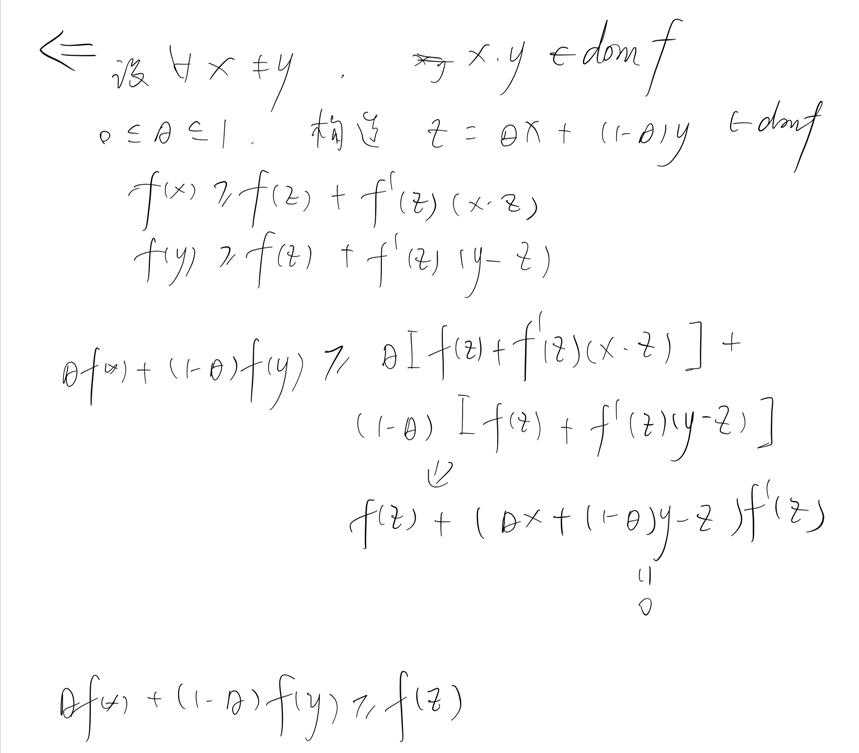


一些常见函数
二次函数
\\[f: R^n \\leftarrow R, dom f \\in R^n\\]
\\[f(x)=\\frac12x^TPx + q^Tx + r\\]
求其黑塞矩阵:\\(\\bigtriangledown^2 f(x)=P\\),当\\(P>0\\)的时候,二次函数就是凸函数。
分数函数
\\[f(x)=\\frac1x^2, x \\not= 0, x \\in R\\]
其二阶倒数\\(f^``(x)=6x^-4>0\\),虽然二阶导大于0,但是这个函数并不是凸函数。主要原因是因为:要定义域是凸集,且二阶导大于0的函数才是凸函数。这里定义域不是凸集。
仿射函数
\\[f(x)=Ax + b, \\bigtriangledown^2f(x)=0\\]
故仿射函数即时凸函数,也是凹函数。
指数函数
\\[f(x)=e^ax, x\\in R\\]
\\[f^``(x)=a^2 e^ax > 0\\]
故指数函数是凸函数。
幂函数
\\[f(x)=x^a, x \\in R_++\\]
\\[f^``(x)=a(a-1)x^a-2\\]
\\[
\\bigtriangledown^2f(x) =
\\begincases
\\geq 0, a \\geq 1 或 a \\leq 0 \\ \\leq 0, 0 \\leq a \\leq 1
\\endcases
\\]
绝对值幂函数
\\[f(x) = |x|^p, x\\in R\\]
\\[ f^``(x) = \\begincases p(p-1)x^p-2, x \\geq 0 \\ p(p-1)(-x)^p-2, x < 0 \\endcases \\]
当\\(p\\geq 1\\)时,该函数为凸函数。
对数函数
\\[f(x)=log(x), x\\in R_++\\]
- 凹函数
负熵
\\[f(x)=xlogx , x \\in R_++\\]
- 凸函数
范数
下面给出范数的定义:
\\(R^n\\)空间的范数\\(p(x), x\\in R^n\\),满足三个性质:
- \\(p(ax)=|a|p(x)\\)
- \\(p(x+y) \\leq p(x)+p(y)\\)
- \\(p(x)=0 \\leftrightarrows x=0\\)
- 范数函数是凸函数。
零范数
零范数的定义是:\\(||x||_0=非零元素的数目\\)
- 该函数虽然名字有叫范数,但它不是范数,也不是凸函数。
极大值函数

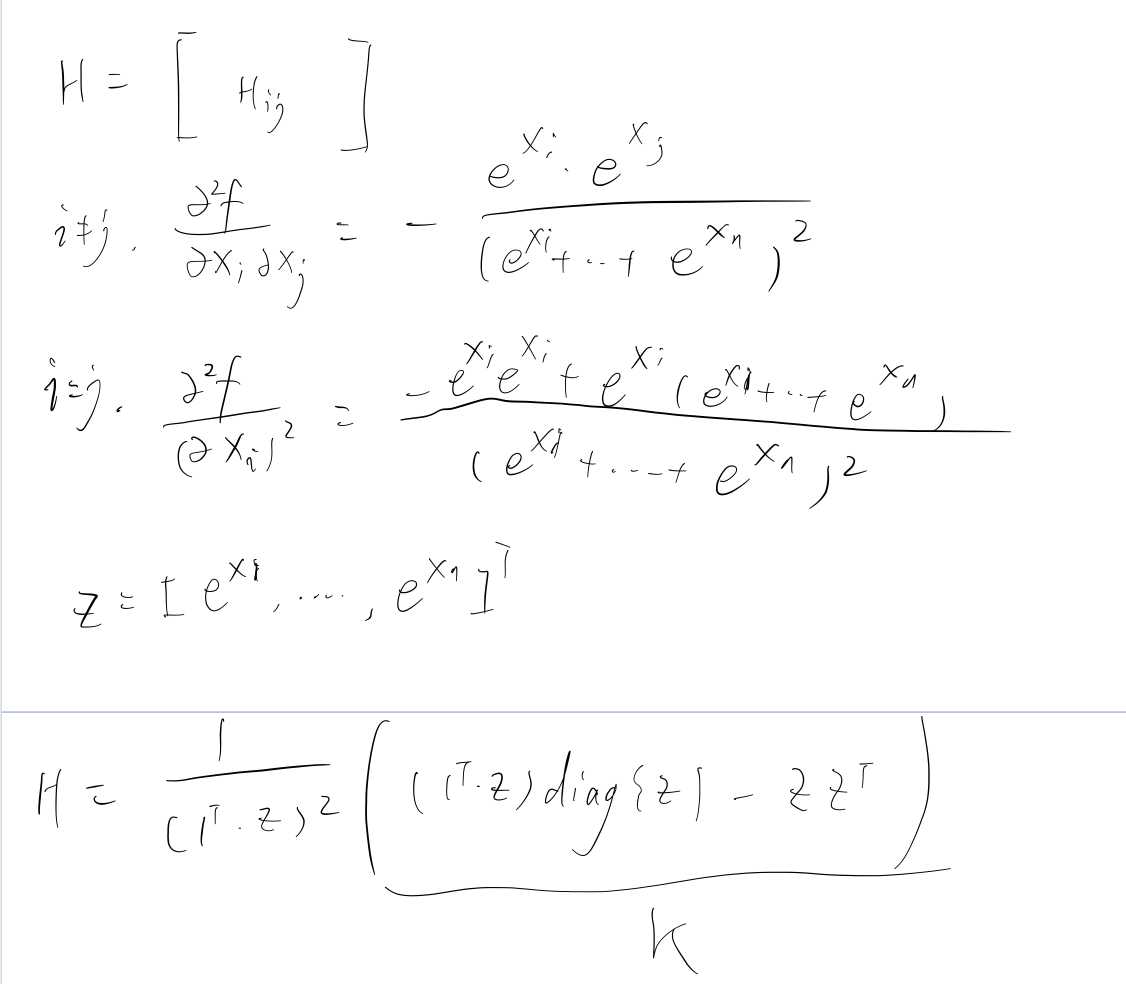

以上是关于凸优化4 凸函数的主要内容,如果未能解决你的问题,请参考以下文章