凸集,凸函数,凸优化问题。
Posted szqfreiburger
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了凸集,凸函数,凸优化问题。相关的知识,希望对你有一定的参考价值。
最近学习了一些凸优化的知识,想写几篇随笔作为总结备忘。在此篇中我们简要地介绍一点点基本概念。
1. 凸集
??定义1. 集合\\(S\\in\\mathbbR^n(n\\geq 1)\\) 被称为是凸集,如果对于任意的\\(x,y\\in S\\),\\(t\\in (0,1)\\)则 \\(tx+(1-t)y\\in S\\)
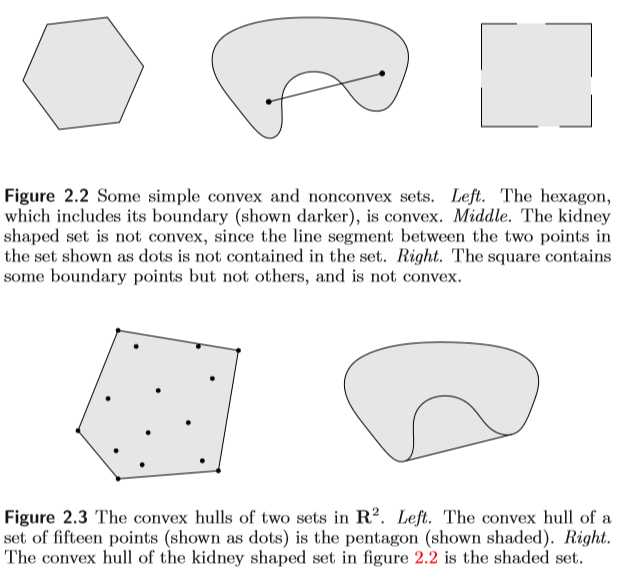
Figure 1. 一些凸集和非凸集的简单例子
2. 仿射集
??定义2. 集合\\(S\\in\\mathbbR^n(n\\geq 1)\\) 被称为是仿射集,如果对于任意的\\(x,y\\in S, x\\neq y\\),\\(t\\in \\mathbbR\\)则 \\(tx+(1-t)y\\in S\\)
由定义我们容易知道,仿射集只不过是由线性空间平移得到的集合,自然也是凸集。
??定义3. 我们称任意集合\\(S\\in\\mathbbR^n(n\\geq 1)\\) 的仿射包为所有包含\\(S\\)的仿射集合中最小的那一个集合,记其为\\(Aff\\; S\\)。
由定义我们很容易知道对于任意集合\\(S\\in\\mathbbR^n(n\\geq 1)\\), 我们有:
\\[Aff\\; S=\\lbrace t_1x_1+...+t_kx_k\\mid t_1,...,t_k\\in\\mathbbR,x_1,...,x_k\\in S, k\\geq 1\\rbrace\\]
??除此以外,我们也会在后续接触到一个重要概念:“相对内部”(Relative Interior)。现在若\\(S\\in\\mathbbR^n\\)是某一子集,\\(Aff \\ S\\)是\\(S\\)的仿射包,则\\(Aff \\ S\\)自然有由\\(\\mathbbR^n\\)诱导的拓扑结构。现在我们定义:
??定义4. 我们称\\(S\\)作为\\(Aff \\: S\\)的子集在\\(Aff \\:S\\)中其诱导拓扑意义下的内部称为相对内部,记作relint:S。
定义4看着有点古板而拗口,其实它的意思也就是"\\(S\\) 在 \\(Aff\\:S\\)中的内部,不是更大的\\(\\mathbbR^n\\)中的内部"。例如对\\(\\mathbbR^n\\)中任意的维度严格小于\\(n\\)的仿射子集\\(A\\),我们知道其在\\(\\mathbbR^n\\)中的内部\\(int A\\)为空,但是其相对内部\\(relint A\\)就是\\(A\\)自身。
3.凸函数
??设某函数\\(f\\)的定义域\\(dom(f)\\in\\mathbbR^n\\)是一个凸集,我们称该函数时一个凸函数如果对于任意的\\(x,y\\in dom(f)\\), \\(t\\in (0,1)\\)有:
\\beginequation
f(tx+(1-t)y)\\leq tf(x)+(1-t)f(y)
\\endequation
??我们容易由泰勒展开公式证明如下结论:
定理1(凸函数的一二阶导数刻画):如果函数\\(f\\)的定义域\\(dom(f)\\in\\mathbbR^n\\) 是一凸的开集,且\\(f\\)在其上可微,则\\(f\\)是凸函数dang且仅当:对任意的\\(x,y\\in dom(f)\\)成立有:
\\beginequation
f(y)\\geq f(x)+(y-x)\\cdot \\nabla f(x).
\\endequation
??进一步如果\\(f\\)二阶可微,则\\(f\\)凸当且仅当对任意\\(x\\in dom(f)\\), \\(f\\)在\\(x\\)处的\\(Hessian\\)矩阵\\(Hess(f)(x)\\triangleq (\\frac\\partial^2f(x)\\partial x_i\\partial x_j)_n\\times n\\)非负定。
4.凸优化问题
??现在我们考虑一类极值(优化)问题:
\\beginequation\\beginsplit\\textmin\\quad & f_0(x) \\newline \\textsubject to:\\quad & f_i(x)\\leq 0, i=1,...,m \\newline & h_i(x)=0, i=1,...,p\\endsplit\\endequation
??其中我们称函数\\(f_0: dom(f_0)\\in \\mathbbR^n\\longrightarrow \\mathbbR\\) 为目标函数,而其后所跟随的不等号条件\\(f_i(x)\\leq 0, i=1,2,...,m\\)为不等式约束条件,\\(f_i: dom(f_i)\\longrightarrow \\mathbbR\\)\\((i=1,...,m)\\)为不等式约束函数,等号条件\\(h_i(x)=0,i=1,...,p\\)为等式约束条件,相应的\\(h_i: dom(h_i)\\longrightarrow \\mathbbR\\)称为等式约束函数, 我们统称这些条件为约束条件,这些函数为约束函数。
??在以后的讨论中我们都用\\(D\\)表示定义域\\(dom(f_i),i=0,...,m\\), \\(dom(h_i),i=1,...,p\\)的交集, 而记集合\\(C=\\lbrace x\\in D\\mid f_i(x)\\leq 0,i=1,...,m, h_i(x)=0,i=1,...,p\\rbrace\\),称其为优化问题(3)的可行域。注意到,\\(C\\)可能会是空集。同时,我们记\\(p^\\ast=inf_x\\in Cf_0(x)\\), 称其为最优化问题(3)的最优值。注意到,该最优值不一定能达到, 并且当可行域\\(C\\)为空集的时候\\(p^\\ast=+\\infty\\)。 如果\\(x^\\ast\\in C\\), \\(f_0(x^\\ast)=p^\\ast\\), 我们称\\(x^\\ast\\)为最优化问题(3)的最优解。
所谓的凸优化问题就是(3)中\\(f_0,...,f_m\\), \\(h_1,...,h_p\\)均为凸函数而\\(h_1,...,h_p\\)均为仿射函数的最优化问题。我们将在以后的随笔中重地讨论之。
以上是关于凸集,凸函数,凸优化问题。的主要内容,如果未能解决你的问题,请参考以下文章