机器学习凸集凸函数凸优化凸优化问题非凸优化问题概念详解

Posted 2021-09-24 Better Bench

目录

• 1 基本概念
• 2 凸优化问题
• 3 非凸优化问题
• 4 总结

1 基本概念

（1）凸集和非凸集
凸集是一个点集， 这个点集有一个性质， 就是在这个集合中任取不同的两个点x和y， 他们之间的线段（包括端点）上的点都属于这个点集，那么就说这个点集是一个凸集。比如下图中左边的图形是凸集，而右边就是非凸集，因为可以找到两个点，使它们之间的线段上的点不在集合中

（3）凸函数(Convex function)和非凸函数(Convave function)
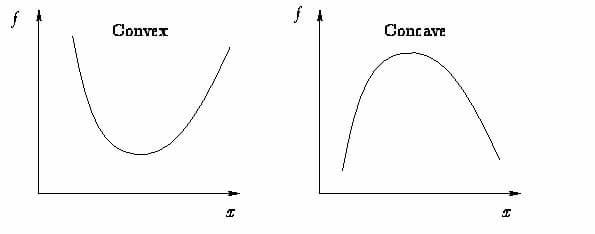
通常把函数分为凸函数和非凸函数。凸函数的几何意义在于，定义域中任意两点连线组成的线段都在这两点的函数曲线（面）上方。如图所示。凸函数是有且只有全局最优解的，而非凸函数可能有多个局部最优解。

判定方法：

• 对于一元函数f(x)，首先必须定义域是凸集，其次通过其二阶导数f′′(x) 的符号来判断。如果函数的二阶导数总是非负，即f′′(x)≥0 ，则f(x)是凸函数。
• 对于多元函数f(X)，首先必须定义域是凸集，其次通过其Hessian矩阵（Hessian矩阵是由多元函数的二阶导数组成的方阵）的正定性来判断。如果Hessian矩阵是半正定矩阵，则是f(X)凸函数。

（4）凸优化和非凸优化
在最小化（最大化）的优化要求下，目标函数是凸函数且约束条件所形成的可行域集合是一个凸集的优化方法，因此凸优化的判定条件有两个

• 函数定义域是凸集
• 目标函数是凸函数

（4）水平子集(sublevel sets)
由凸函数的概念出发，我们可以引出水平子集（sublevel set）的概念。假定f(x)是一个凸函数， 给定一个实数α∈R，我们把集合
{ x ( f ) ∣ f ( x ) ≤ α } \\{ x(f)| f(x) \\leq \\alpha \\} {x(f)∣f(x)≤α}
叫做α−水平子集。 也就是说α水平子集是所有满足f(x)≤α的点构成的集合。利用凸函数性质，我们可以证明水平子集也是凸集：
$$f(\theta x+(1-\theta y))\le \theta f(x)+(1-\theta )f(y)\le \theta \alpha +(1-\theta )\alpha$$
水平子集告诉我们，给凸函数添加一个上限，定义域内剩下的点构成的点集还是一个凸集。
（5）仿射函数(affine functions)
数学上，我们把形如
$$h(x)=Ax+b$$
的函数叫做仿射函数。其中，A是一个m*n的矩阵，x是一个k向量，b是一个m向量。直观上理解，仿射函数将一个n维空间的向量通过线性变换A映射到m维空间，并在其基础上加上向量b，进行了平移。实际上反映了一种从 k维到m维的空间映射关系。

2 凸优化问题

（1）定义
数学上表示为
$$\begin{gathered} minf(x) \\ s.tx\in C \end{gathered}$$
其中f是凸函数，C是凸集。以下是用仿射函数的表示法
$$\begin{gathered} minf(x) \\ s.t{g}_i(x)\le 0,i=1,...,m \\ {h}_i(x)=0,i=1,..,p \end{gathered}$$
其中g(x)是凸函数，h(x)是仿射函数。原约束集C表示为了一系列凸集的交集。
（2）简介
优化方法是几乎所有机器学习模型中最重要的核心部分，凸优化是优化方法论中的特例，是一个非常大的领域。
例如针对逻辑回归、线性回归这样的凸函数，使用梯度下降或者牛顿法可以求出参数的全局最优解，针对神经网络这样的非凸函数，我们可能会找到许多局部最优解。
（3）经典凸优化问题

• Least squares（最小二乘法，常用，目标：线性关系；限制条件：线性关系）
• Convex quadratic minimization with linear constraints（线性约束条件下的二次规划问题，常用，目标：平方关系；限制条件：线性关系）
• Linear programming（线性规划）
• Quadratic minimization with convex quadratic constraints(具有凸二次约束的二次最小化)
• Conic optimization(圆锥优化)
• Geometric programming(几何规划)
• Second order cone programming(二阶锥规划)
• Semidefinite programming(半定规划)
• Entropy maximization with appropriate constraints(具有适当约束的熵最大化)

3 非凸优化问题

（1）简介
在实际解决问题过程中，都希望我们建立的目标函数是凸函数，这样我们不必担心局部最优解问题，但实际上，我们遇到的问题大多数情况下建立的目标函数都是非凸函数，因此我们需要根据场景选择不同的优化方法。
我们在寻找优化方法论时，一定要选择更合理的方法论。很多非凸优化问题可以转化（并非是等价的）为凸优化问题，并给出问题的近似解。
当非凸优化应用到机器学习中时，目标函数可以允许算法设计者编码适当和期望的行为到机器学习模型中，例如非凸优化中的目标函数可以表示为衡量拟合训练数据好坏的损失函数。正如 Goodfellow 所说，一般的非凸优化和深度学习中的非凸优化，最大的区别就是深度学习不能直接最小化性能度量，而只能最小化损失函数以近似度量模型的性能。而对目标函数的约束条件是允许约束模型编码行为或知识的能力，例如约束模型的大小。
（2）传统解决方法
面对非凸问题及其与 NP-hard 之间的关系，传统的解决方案是修改问题的形式化或定义以使用现有工具解决问题，即凸松弛（Relaxation），对问题限制条件的松弛，将原问题等价为凸优化问题。但是我们求出来的最优解与原问题的最优解可能是相等，也可能有一定的误差的，所以通过relaxation，我们需要证明relaxation得出的最优解和原问题的最优解的误差范围。
由于该方法允许使用类似的算法技术，所谓的凸松弛方法得到了广泛研究。例如，推荐系统和稀疏回归问题都应用了凸松弛方法。对于稀疏线性回归，凸松弛方法带来了流行的 LASSO 回归。
（3）非凸优化方法
机器学习和信号处理领域出现了一种新方法，不对非凸问题进行松弛处理而是直接解决。引起目标是直接优化非凸公式，该方法通常被称为非凸优化方法。非凸优化方法常用的技术包括简单高效的基元（primitives），如投影梯度下降、交替最小化、期望最大化算法、随机优化及其变体。这些方法在实践中速度很快，且仍然是从业者最喜欢用的方法。
如果该问题具备较好的结构，那么不仅可以使用松弛方法，还可以使用非凸优化算法。在这类案例中，非凸方法不仅能避免 NP-hard，还可以提供可证明的最优解。事实上，在实践中它们往往显著优于基于松弛的方法，不管是速度还是可扩展性

4 总结

当我们拿到一个业务问题，一定需要按照算法思维去做，先将问题转换为一个严谨的数学问题，判断我们写出的目标函数的凹凸性，如果目标函数非凸，我们需要对问题的限制条件做一些转化，进而求出转化后问题的近似解，并证明其与原问题的误差范围。如果是凸函数，我们需要选择相应的优化方法论进行优化，因为优化问题是机器学习算法中的核心部分。