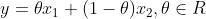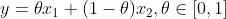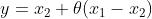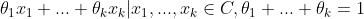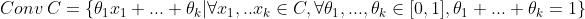凸优化——仿射集合凸集凸锥

Posted 2021-12-21 码丽莲梦露

目录

1 仿射集合、凸集、凸锥

1.1 直线和线段

​1.2 仿射集合、组合、仿射包

1.3 凸集、凸组合

1.4 锥

---

1 仿射集合、凸集、凸锥

1.1 直线和线段

        设空间中两个点,那么直线和线段可以表示为：

直线：

线段：

y还可以写成：

1.2 仿射集合、组合、仿射包

        如果通过集合中任意两个不同点的直线仍然在集合C中中，那么称集合C是仿射的，即：

对于任意有.

换言之，C包含了C中任意两点的系数之和为1的线性组合

 扩展到多个点的情况，如果,我们称具有形式的点为的仿射组合，即：

如果C是仿射集合，，并且，那么仍在C中。

证明：

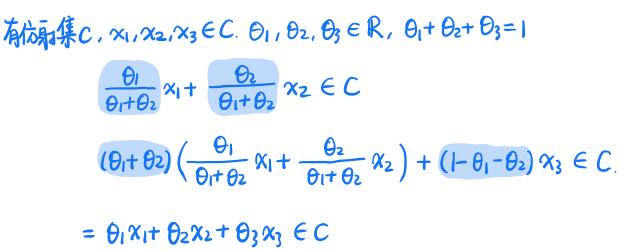
仿射集合的子空间：

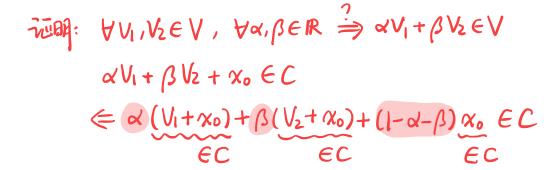
 我们称由集合中所有点的所有仿射组合组成的集合为C的仿射包，记作aff C:

aff C=

 仿射包是包含C的最小的仿射集合。

1.3 凸集、凸组合

        集合C被称为凸集，如果C中任意两点间的线段仍在C中，即对于任意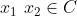和θ∈[0,1]有：

粗略的，如果集合中每一点都可以被其他点沿着它们之间一条无阻碍的路径看见，那么这个集合就是凸集。 所谓无阻碍即整条路径都在集合中。

凸组合：

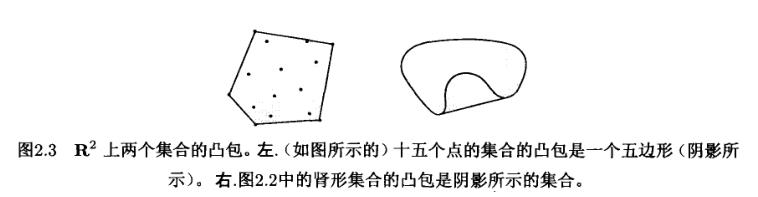
凸包：

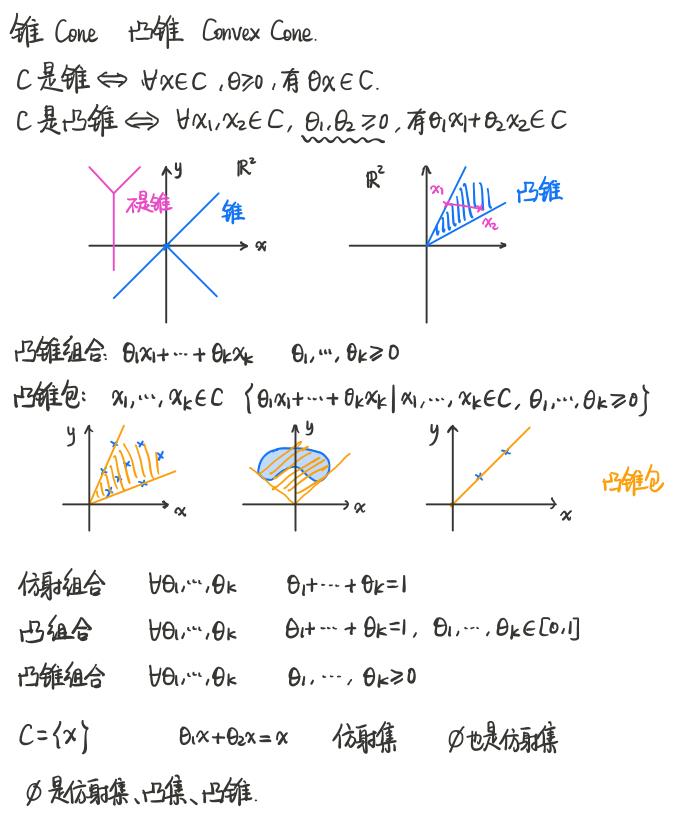
 1.4 锥