优化理论02----凸函数共轭函数拟凸函数对数凹/对数凸函数关于广义不等关系的凸性
Posted 炫云云
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了优化理论02----凸函数共轭函数拟凸函数对数凹/对数凸函数关于广义不等关系的凸性相关的知识，希望对你有一定的参考价值。
1 基本性质和例子
定 义 \\large\\color{#70f3ff}{\\boxed{\\color{brown}{定义 } }} 定义
一个函数
f
:
R
n
→
R
f: R^n\\rightarrow R
f:Rn→R 是凸的，如果定义域
d
o
m
f
dom\\,f
domf 是凸集，并且对于所有
x
,
y
∈
f
,
θ
≤
1
x,y\\in f, \\theta\\leq 1
x,y∈f,θ≤1 ，我们有
f
(
θ
x
+
(
1
−
θ
)
y
)
≤
θ
f
(
x
)
+
(
1
−
θ
)
f
(
y
)
(1)
f(\\theta x+(1-\\theta)y)\\leq \\theta f(x)+(1-\\theta)f(y)\\tag1
f(θx+(1−θ)y)≤θf(x)+(1−θ)f(y)(1)
几何解释：点 ( x , f ( x ) ) (x,f(x)) (x,f(x)) 和 ( y , f ( y ) ) (y,f(y)) (y,f(y)) 之间的线段在 f f f 对应的图像上方。
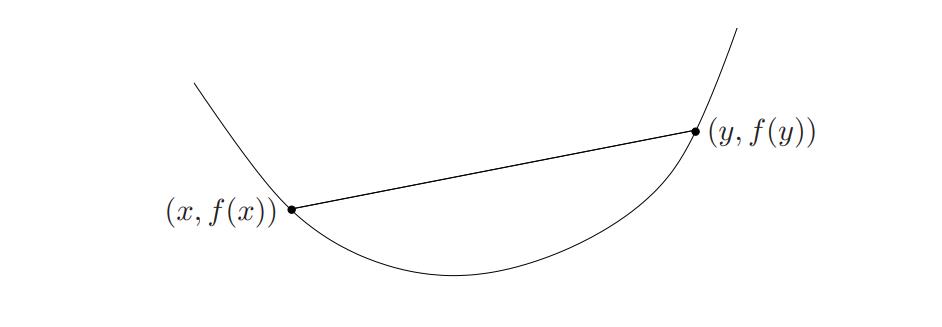
凸 函 数 的 图 表 示 。 函 数 上 任 意 两 点 之 间 的 弦 ( 即 线 段 ) 位 于 函 数 的 上 方 。 凸函数的图表示。函数上任意两点之间的弦(即线段)位于函数的上方。 凸函数的图表示。函数上任意两点之间的弦(即线段)位于函数的上方。
-
函数 f f f 是严格凸的，则不等式(1)在 x ≠ y x\\ne y x=y ，且 0 < θ < 1 0<\\theta <1 0<θ<1 时严格成立.
-
函数 f f f 是凹的，当 − f -f −f 是凸的，严格凹，当 − f -f −f 是严格凸的。
-
仿射函数既是凸的也是凹的，反过来，既凹又凸的函数是仿射的。
-
一个函数 f f f 是凸的当且仅当对任意 x ∈ d o m f x\\in dom\\,f x∈domf 和任意 v v v ，函数 g ( t ) = f ( x + t v ) g(t)=f(x+tv) g(t)=f(x+tv) 是凸的， { t ∣ x + t v ∈ d o m f } . \\{t|x+tv\\in dom\\,f\\}. {t∣x+tv∈domf}.这个性质非常有用，因为它允许我们通过将一个函数限定为一条直线来检查它是否为凸函数。
-
函数 f ( x ) : C → R f (x): C→R f(x):C→R，其中 C C C是非空凸集，如果是凹函数,则有
f ( θ x + ( 1 − θ ) y ) ≥ θ f ( x ) + ( 1 − θ ) f ( y ) f(\\theta x+(1-\\theta)y)\\geq \\theta f(x)+(1-\\theta)f(y) f(θx+(1−θ)y)≥θf(x)+(1−θ)f(y)
一个凸函数在其域的相对内部是连续的;它只能在其相对边界上有不连续。
扩 展 值 扩 展 \\large\\color{#70f3ff}{\\boxed{\\color{brown}{扩展值扩展 } }} 扩展值扩展
将凸函数扩展到整个
R
n
R^n
Rn ，通常令它在定义域之外取
∞
\\infty
∞ 。如果
f
f
f 是凸函数那么它的拓展为
f
~
:
R
n
→
R
∪
{
∞
}
\\widetilde{f} : R^n\\rightarrow R \\cup \\{\\infty\\}
f
:Rn→R∪{∞} ,扩展值定义：
f
~
(
x
)
=
{
f
(
x
)
x
∈
d
o
m
f
∞
x
∉
d
o
m
f
\\widetilde{f}(x)=\\left \\{\\begin{aligned} f(x)\\;\\; x\\in domf\\\\ \\infty\\;\\; x\\not\\in domf \\end{aligned}\\right.
f
(x)={f(x)x∈domf∞x∈domf
如果函数
f
:
R
n
→
R
f: \\textbf{R}^n \\rightarrow \\textbf{R}
f:Rn→R 是凹函数，定义其延拓（extended-value extentions）为
f
~
:
R
n
→
R
∪
{
−
∞
}
\\tilde{f}: \\textbf{R}^n \\rightarrow \\textbf{R} \\cup \\{ -\\infty\\}
f~:Rn→R∪{−∞} :
f
~
(
x
)
=
{
f
(
x
)
x
∈
dom
f
−
∞
x
∉
dom
f
.
\\tilde{f}(x) =\\left\\{\\begin{array}{ll} f(x) &x \\in \\textbf{dom}f\\\\ -\\infty &x \\notin \\textbf{dom}f. \\end{array}\\right.
f~(x)={f(x)−∞x∈domfx∈/domf.
这样拓展后，不需要每次指出
x
∈
dom
f
x \\in \\textbf{dom}f
x∈domf
一 阶 条 件 \\large\\color{#70f3ff}{\\boxed{\\color{brown}{一阶条件 } }} 一阶条件
令函数 f f f 是可微的（也就是它的梯度 ∇ f \\nabla f ∇f 在开集的 d o m f dom\\,f domf每个点上都存在）。那么 f f f 是凸的，充要条件是 d o m f dom\\,f domf是凸的，并且对所有的 x , y ∈ d o m f x,y\\in dom~f x,y∈dom f 有：
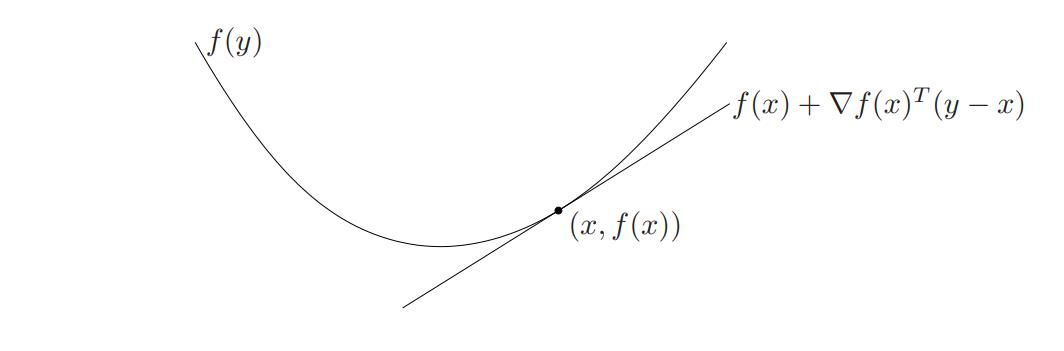
f ( y ) ≥ f ( x ) + ∇ f ( x ) T ( y − x ) (2) f(y)\\geq f(x)+\\nabla f(x)^T(y-x)\\tag{2} f(y)≥f(x)+∇f(x)T(y−x)(2)
在每个点上，函数图像都高于在该点的切线。
如果 f f 以上是关于优化理论02----凸函数共轭函数拟凸函数对数凹/对数凸函数关于广义不等关系的凸性的主要内容，如果未能解决你的问题，请参考以下文章
最优化之凸集凸函数上确界Jensen不等式共轭函数Fenchel不等式拉格朗日乘子法KKT条件