[傅里叶变换及其应用学习笔记] 二十九. 高维Ш函数修改版

Posted 2020-06-12

 

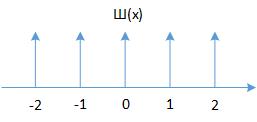
一维Ш函数复习

我们前面（十六课，十七课）已经学习过一维的Ш函数，标准的Ш函数表现为无数个脉冲函数分布在整数点上，

我们定义Ш为

$Ш(x) = \\displaystyle{ \\sum_{k=-\\infty}^{\\infty}\\delta(x-k) }$

而Ш函数最为深刻的一个性质就是：Ш的傅里叶变换是它自身

$\\mathcal{F}Ш=Ш$

 

 

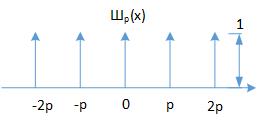
进一步推广到脉冲间隔为$p$的函数$Ш_p$

$\\displaystyle{ Ш_p(x)=\\sum_{k=-\\infty}^{\\infty}\\delta(x-kp) }$

它的傅里叶变换中有两处出现了倒数：幅度为$\\frac{1}{p}$，频域的脉冲间隔也变为了$\\frac{1}{p}$

$\\mathcal{F}Ш_p=\\frac{1}{p}Ш_{\\frac{1}{p}}$

 

 

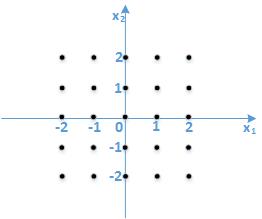
二维Ш函数$Ш_{\\mathbb{Z}^2}$

标准的二维Ш函数同样也是分布在二维平面的整数点上的脉冲函数

这些二维的整数点组成了二维平面上的整数晶格，用$\\mathbb{Z}^2$表示（integer lattice in the plane denote by $\\mathbb{Z}^2$）。二维的Ш函数就是在此晶格的每个点上都有一个脉冲函数

$\\displaystyle{ Ш_{\\mathbb{Z}^2}(\\underline{x})=\\sum_{\\underline{k}\\in \\mathbb{Z}^2}\\delta(\\underline{x}-\\underline{k}) }$

它的傅里叶变换的推导需要依据二维的泊松求和公式

 

 

二维泊松求和公式

二维泊松求和公式与一维的泊松求和公式的推导过程基本上是一样的。标准的二维Ш函数$Ш_{\\mathbb{Z}^2}$，是一个以$\\underline{e}_1=(1,0),\\underline{e}_2=(0,1)$为基准向量的周期函数

把$Ш_{\\mathbb{Z}^2}$分解为傅里叶级数的形式，有

$\\begin{align*}
Ш_{\\mathbb{Z}^2}(\\underline{x})
&=\\sum_{\\underline{k}\\in\\mathbb{Z}^2}C_{\\underline{k}}e^{2\\pi i\\underline{k}\\cdot\\underline{x}}\\\\
&=\\sum_{\\underline{k}\\in\\mathbb{Z}^2}\\left( \\int_{\\underline{0}}^{\\underline{1}}Ш_{\\mathbb{Z}^2}(\\underline{x})e^{-2\\pi i\\underline{k}\\cdot\\underline{x}}d\\underline{x} \\right )e^{2\\pi i\\underline{k}\\cdot\\underline{x}}\\\\
&=\\sum_{\\underline{k}\\in\\mathbb{Z}^2}\\left( \\int_{\\underline{0}}^{\\underline{1}}\\delta(\\underline{x})e^{-2\\pi i\\underline{k}\\cdot\\underline{x}}d\\underline{x} \\right )e^{2\\pi i\\underline{k}\\cdot\\underline{x}}\\\\
&=\\sum_{\\underline{k}\\in\\mathbb{Z}^2}e^{-2\\pi i\\underline{k}\\cdot\\underline{0}}e^{2\\pi i\\underline{k}\\cdot\\underline{x}}\\\\
&=\\sum_{\\underline{k}\\in\\mathbb{Z}^2}e^{2\\pi i\\underline{k}\\cdot\\underline{x}}
\\end{align*}$

因此

$\\displaystyle{ \\sum_{\\underline{k}\\in\\mathbb{Z}^2}C_{\\underline{k}}e^{2\\pi i\\underline{k}\\cdot\\underline{x}}=\\sum_{\\underline{k}\\in\\mathbb{Z}^2}e^{2\\pi i\\underline{k}\\cdot\\underline{x}} }$

 

有了这样的条件，我们就可以进行以下推导泊松公式

$\\begin{align*}
\\sum_{\\underline{k}\\in \\mathbb{Z}^2}\\mathcal{F}f(\\underline{k})
&=\\sum_{\\underline{k}\\in \\mathbb{Z}^2}\\left( \\int_{\\mathbb{R}^2}f(\\underline{x})e^{-2\\pi i\\underline{k}\\cdot\\underline{x}}d\\underline{x} \\right )\\\\
&=\\int_{\\mathbb{R}^2}f(\\underline{x})\\left(\\sum_{\\underline{k}\\in \\mathbb{Z}^2}e^{-2\\pi i\\underline{k}\\cdot\\underline{x}} \\right )d\\underline{x}\\\\
&=\\int_{\\mathbb{R}^2}f(\\underline{x})\\left(\\sum_{\\underline{k}\\in \\mathbb{Z}^2}e^{2\\pi i\\underline{k}\\cdot\\underline{x}} \\right )d\\underline{x}\\\\
&=\\int_{\\mathbb{R}^2}f(\\underline{x})\\left(\\sum_{\\underline{k}\\in \\mathbb{Z}^2}\\delta(\\underline{x}-\\underline{k}) \\right )d\\underline{x}\\\\
&=\\sum_{\\underline{k}\\in\\mathbb{Z}^2}\\left(\\int_{\\mathbb{R}^2}f(\\underline{x})\\delta(\\underline{x}-\\underline{k})d\\underline{x} \\right )\\\\
&=\\sum_{\\underline{k}\\in\\mathbb{Z}^2}f(\\underline{k})
\\end{align*}$

可得二维泊松公式如下

$\\displaystyle{ \\sum_{\\underline{k}\\in \\mathbb{Z}^2}\\mathcal{F}f(\\underline{k})=\\sum_{\\underline{k}\\in\\mathbb{Z}^2}f(\\underline{k}) }$

 

 

$Ш_{\\mathbb{Z}^2}$的傅里叶变换

根据二维的泊松求和公式，$\\mathcal{F}Ш_{\\mathbb{Z}^2}$的求解过程如下

$\\begin{align*}
<\\mathcal{F}Ш_{\\mathbb{Z}^2},\\varphi>
&=<Ш_{\\mathbb{Z}^2},\\mathcal{F}\\varphi>\\\\
&=\\sum_{\\underline{k}\\in\\mathbb{Z}^2}\\mathcal{F}\\varphi(\\underline{k})\\\\
&=\\sum_{\\underline{k}\\in\\mathbb{Z}^2}\\varphi(\\underline{k}) \\qquad (The\\ Possion\\ Sum\\ Formula)\\\\
&=<Ш_{\\mathbb{Z}^2},\\varphi>
\\end{align*}$

即

$\\mathcal{F}Ш_{\\mathbb{Z}^2}=Ш_{\\mathbb{Z}^2}$

 

 

$Ш_{\\mathbb{Z}^2}$的周期化特性

$Ш_{\\mathbb{Z}^2}$的周期化特性源自于$\\delta$的移位特性，通过卷积实现

$\\Phi(\\underline{x})=(\\varphi*A_{\\mathbb{Z}^2})(\\underline{x})=\\displaystyle{ \\sum_{\\underline{k}\\in\\mathbb{Z}^2}\\varphi(\\underline{x}-\\underline{k}) }$

$\\Phi(\\underline{x}+\\underline{k}) = \\Phi(\\underline{x}) \\qquad \\underline{k}\\in\\mathbb{Z}^2 $

 

 

 

$Ш_{\\mathbb{Z}^2}$的采样特性

$Ш_{\\mathbb{Z}^2}$的采样特性同样源自于$\\delta$的采样特性

$(\\varphi Ш_{\\mathbb{Z}^2})(\\underline{x})=\\displaystyle{ \\sum_{\\underline{k}\\in\\mathbb{Z}^2}\\varphi(\\underline{k})\\delta(\\underline{x}-\\underline{k}) }$

 

 

 

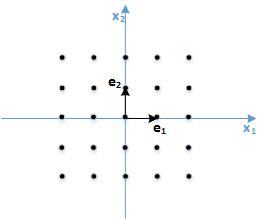
一般化的二维Ш函数$Ш_{\\mathcal{L}}$

对于标准的二维Ш函数

$\\displaystyle{ Ш_{\\mathbb{Z}^2}(\\underline{x})=\\sum_{\\underline{k}\\in\\mathbb{Z}^2}\\delta(\\underline{x}-\\underline{k}) }$

式子当中的向量$\\underline{k}$位于二维平面的整数点上，因此$\\underline{k}$可以看作是基准向量$\\underline{e}_1=(1,0),\\underline{e}_2=(0,1)$整数倍的组合

$\\underline{k}=k_1\\underline{e}_1+k_2\\underline{e}_2$

 

一维的Ш函数函数可以一般化为$Ш_p$，即各脉冲的距离为$p$，而二维的Ш函数则有更高的自由度，可以通过改变两个基准向量（缩放，旋转），从而表示一般的Ш函数

图中$\\underline{u}_1,\\underline{u}_2$分别作为基向量，他们的整数倍组合成了向量$\\underline{p}$

$\\underline{p} = k_1\\underline{u}_1+k_2\\underline{u}_2 \\qquad k_1,k_2=0,\\pm 1,\\pm 2$

我们把二维平面上所有这些点组成的晶格用$\\mathcal{L}$来表示，那么一般的二维Ш函数为：

$Ш_{\\mathcal{L}}(\\underline{x}) = \\displaystyle{\\sum_{\\underline{p}\\in\\mathcal{L}}\\delta(\\underline{x}-\\underline{p})=\\sum_{k_1,k_2=-\\infty}^{\\infty}\\delta(\\underline{x}-k_1\\underline{u}_1-k_2\\underline{u}_2) }$

 

晶格$\\mathcal{L}$可以通过对晶格$\\mathbb{Z}^2$进行线性变换来得到，也就是说$\\underline{u}_1,\\underline{u}_2$可以通过$\\underline{e}_1,\\underline{e}_2$的线性变换得到，令线性变换矩阵为$A$，有

$\\underline{u}_1=A\\underline{e}_1 \\qquad \\underline{u}_2=A\\underline{e}_2$

把它代入$Ш_{\\mathcal{L}}$，有

$\\displaystyle{ Ш_{\\mathcal{L}}(\\underline{x}) = \\sum_{k_1,k_2=-\\infty}^{\\infty}\\delta(\\underline{x}-k_1A\\underline{e}_1-k_2A\\underline{e}_2)=\\sum_{\\underline{k}\\in\\mathbb{Z}^2}\\delta(\\underline{x}-A\\underline{k}) }$

 

 

$Ш_{\\mathcal{L}}$的傅里叶变换

首先需要把$Ш_{\\mathcal{L}}$转换成$Ш_{\\mathbb{Z}^2}$的形式

$\\begin{align*}
Ш_{\\mathcal{L}}(\\underline{x})
&=\\sum_{\\underline{k}\\in\\mathbb{Z}^2}\\delta(\\underline{x}-A\\underline{k})\\\\
&=\\sum_{\\underline{k}\\in\\mathbb{Z}^2}\\delta(A(A^{-1}\\underline{x}-\\underline{k}))\\\\
&=\\sum_{\\underline{k}\\in\\mathbb{Z}^2}\\frac{1}{|detA|}\\delta(A^{-1}\\underline{x}-\\underline{k}) \\qquad \\delta\\ scaling\\ property\\\\
&=\\frac{1}{|detA|}\\sum_{\\underline{k}\\in\\mathbb{Z}^2}\\delta(A^{-1}\\underline{x}-\\underline{k}) \\\\
&=\\frac{1}{|detA|}Ш_{\\mathbb{Z}^2}(A^{-1}\\underline{x})
\\end{align*}$

 

对$Ш_{\\mathcal{L}}$进行傅里叶变换，有

$\\begin{align*}
\\mathcal{F}Ш_{\\mathcal{L}}
&=\\frac{1}{|detA|}\\mathcal{F}(Ш_{\\mathbb{Z}^2}(A^{-1}\\underline{x}))\\\\
&=\\frac{1}{|detA|}\\frac{1}{|detA^{-1}|}(\\mathcal{F}Ш_{\\mathbb{Z}^2})(A^{T}\\underline{\\xi}) \\qquad (Fourier\\ scaling\\ theorem)\\\\
&=(\\mathcal{F}Ш_{\\mathbb{Z}^2})(A^{T}\\underline{\\xi}) \\\\
&=Ш_{\\mathbb{Z}^2}(A^{T}\\underline{\\xi})
\\end{align*}$

即有

$\\mathcal{F}Ш_{\\mathcal{L}}(\\underline{\\xi})=Ш_{\\mathbb{Z}^2}(A^{T}\\underline{\\xi})$

 

我们希望把傅里叶变换的结果表达成$\\mathcal{L}$相关的形式，有

$\\begin{align*}
Ш_{\\mathbb{Z}^2}(A^{T}\\underline{\\xi})
&=\\sum_{\\underline{k}\\in\\mathbb{Z}^2}\\delta(A^{T}\\underline{\\xi}-\\underline{k})\\\\
&=\\sum_{\\underline{k}\\in\\mathbb{Z}^2}\\delta(A^{T}(\\underline{\\xi}-A^{-T}\\underline{k}))\\\\
&=\\frac{1}{|detA^T|}\\sum_{\\underline{k}\\in\\mathbb{Z}^2}\\delta(\\underline{\\xi}-A^{-T}\\underline{k}) \\qquad (\\delta\\ scaling\\ property)\\\\
&=\\frac{1}{|detA|}\\sum_{\\underline{k}\\in\\mathbb{Z}^2}\\delta(\\underline{\\xi}-A^{-T}\\underline{k})\\\\
&=\\frac{1}{|detA|}Ш_{\\mathcal{L}^*}(\\underline{\\xi})  \\quad\\qquad  \\begin{cases}
Ш\\underline{k} & \\rightarrow \\mathcal{L} \\\\
Ш^{-T}\\underline{k} & \\rightarrow \\mathcal{L}^*
\\end{cases}
\\end{align*}$

其中晶格$\\mathcal{L}$对应$\\mathbb{Z}^2$以矩阵$A$进行转换，晶格$\\mathcal{L}^*$对应$\\mathbb{Z}^2$以矩阵$A^{-T}$进行转换。

 

另外，我们可以对$\\frac{1}{|detA|}$做进一步的解读。

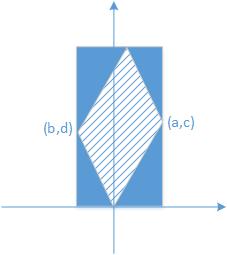
假设$A=\\begin{bmatrix} a &b \\\\ c &d \\end{bmatrix}$，则

$\\underline{u}_1=A\\underline{e}_1 = \\begin{bmatrix} a &b \\\\ c &d \\end{bmatrix}\\begin{bmatrix}1 \\\\ 0\\end{bmatrix}=\\begin{bmatrix} a \\\\ c \\end{bmatrix}$

$\\underline{u}_2=A\\underline{e}_2 = \\begin{bmatrix} a &b \\\\ c &d \\end{bmatrix}\\begin{bmatrix}0 \\\\ 1\\end{bmatrix}=\\begin{bmatrix} b \\\\ d \\end{bmatrix}$

$|detA| = |ad-bc|$

 

其晶格在坐标轴上表示为

单位平行四方形的面积计算如下

$\\begin{align*}
Area(\\mathcal{L})
&=(|a|+|b|)(|c|+|d|)-|bd|-|ac|\\\\
&=|ad|+|bc|\\\\
&=|ad-bc|\\\\
&=|detA|
\\end{align*}$

 

同理可得

$Area(\\mathcal{L}^*)=\\frac{1}{|detA|}$

 

那么最终有

$\\mathcal{F}Ш_{\\mathcal{L}}=Area(\\mathcal{L}^*)Ш_{\\mathcal{L}^*}$

$\\mathcal{L}$与$\\mathcal{L}^*$分别对应矩阵$A$与$A^{-T}$

 

 

 

二维采样定理

一维采样定理

我们在前面的课程中分析过一维的采样定理，这里再次复习一遍

设有带宽为$p$的函数$f(t)$，在频域对这个函数用$Ш_p$进行周期化后，再用$\\Pi_p$对它进行裁剪，得到的还是原来的函数

$\\mathcal{F}f = \\Pi_p(\\mathcal{F}f*Ш_p)$

最终推导得到

$f(t) = \\displaystyle{\\sum_{k=-\\infty}^{\\infty}f(\\frac{k}{p})sinc \\left(p(t-\\frac{k}{p})\\right) }$

在上式中，$p$可被称为抽样速率，即每秒的抽样数目。同时$p$也被称为奈奎斯特速率（Nyquist rate）。

 

 

标准受限函数采样定理

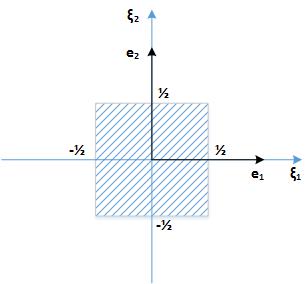
二维采样定理也是采用这种思维进行推导。为了方便推导，我们从频率带宽为$|\\xi_1|<\\frac{1}{2},|\\xi_2|<\\frac{1}{2}$的函数开始进行推导

设有函数$f(\\underline{x})$，它的傅里叶变换$\\mathcal{F}f(\\underline{\\xi})$受限于$|\\xi_1|<\\frac{1}{2},|\\xi_2|<\\frac{1}{2}$

则有

$\\mathcal{F}f(\\underline{\\xi})=\\Pi(\\xi_1)\\Pi(\\xi_2)(\\mathcal{F}*Ш_{\\mathbb{Z}^2})(\\underline{\\xi})$

那么

$\\begin{align*}
f(\\underline{x})
&=\\mathcal{F}^{-1}(\\Pi(\\xi_1)\\Pi(\\xi_2))*\\mathcal{F}^{-1}((\\mathcal{F}*B_{\\mathbb{Z}^2})(\\underline{\\xi}))\\\\
&=(sincx_1sincx_2)*(f(\\underline{x})B_{\\mathbb{Z}^2}(\\underline{x})) \\qquad (Fourier\\ convolution\\ theorem)\\\\
&=(sincx_1sincx_2)*\\left( f(\\underline{x})\\sum_{k_1,k_2=-\\infty}^{\\infty}\\delta(x_1-k_1,x_2-k_2) \\right )\\\\
&=(sincx_1sincx_2)*\\left(\\sum_{k_1,k_2=-\\infty}^{\\infty}f(k_1,k_2)\\delta(x_1-k_1,x_2-k_2) \\right ) \\qquad (\\delta\\ sampling\\ property)\\\\
&=\\sum_{k_1,k_2=-\\infty}^{\\infty}f(k_1,k_2)sinc(x_1-k_1)sinc(x_2-k_2) \\qquad (\\delta\\ shift\\ property)
\\end{align*}$

 

如果我们在其中代入基准向量$\\underline{e}_1=(1,0),\\underline{e}_2=(0,1)$，则可表达为

$\\displaystyle{ f(\\underline{x})=\\sum_{k_1,k_2=-\\infty}^{\\infty}f(k_1\\underline{e}_1+k_2\\underline{e}_2)sinc(\\underline{x}\\cdot\\underline{e}_1-k_1)sinc(\\underline{x}\\cdot\\underline{e}_2-k_2) }$

 

 

一般受限函数采样定理

现在对这个采样定理进行一般化

假设$f(\\underline{x})$在频域上的频谱受限于某平行四边形，那么可以把$f$看作是标准受限的函数在频域上受到了矩阵$A$的作用，即

$\\underline{u}_1=A\\underline{e}_1 \\qquad \\underline{u}_2=A\\underline{e}_2$

 

经过作用后的频谱受限于下图四边形内

下面是推导过程

首先令$g(\\underline{x}) = f(A^{-T}\\underline{x})$，则有

$\\mathcal{F}g(\\underline{\\xi})=\\frac{1}{|detA^{-T}|}\\mathcal{F}f((A^{-T})^{-T}\\underline{\\xi})=|detA|\\mathcal{F}f(A\\underline{\\xi})$

 

由于$f$可以被看作是标准受限的函数在频域上受到了矩阵$A$的作用，如此一来函数$g$就是一个标准受限（受限于$|\\xi_1|<\\frac{1}{2},|\\xi_2|<\\frac{1}{2}$）的函数了。那么函数$g$就能应用上标准受限函数的采样定理，

$\\displaystyle{ g(\\underline{x})=\\sum_{k_1,k_2=-\\infty}^{\\infty}g(k_1\\underline{e}_1+k_2\\underline{e}_2)sinc(\\underline{x}\\cdot\\underline{e}_1-k_1)sinc(\\underline{x}\\cdot\\underline{e}_2-k_2) }$

 

把$g(\\underline{x}) = f(A^{-T}\\underline{x})$代入上述等式，得

$\\displaystyle{ f(A^{-T}\\underline{x})=\\sum_{k_1,k_2=-\\infty}^{\\infty}f(A^{-T}(k_1\\underline{e}_1+k_2\\underline{e}_2))sinc(\\underline{x}\\cdot\\underline{e}_1-k_1)sinc(\\underline{x}\\cdot\\underline{e}_2-k_2) }$

 

令$\\underline{y} = A^{-T}\\underline{x}$，有$\\underline{x}=(A^{-T})^{-1}\\underline{y}=A^{T}\\underline{y}$，那么上面的等式可以转换为

$\\begin{align*}
f(\\underline{y})
&=\\sum_{k_1,k_2=-\\infty}^{\\infty}f\\left(A^{-T}(k_1\\underline{e}_1+k_2\\underline{e}_2)\\right)sinc(A^T\\underline{y}\\cdot\\underline{e}_1-k_1)sinc(A^T\\underline{y}\\cdot\\underline{e}_2-k_2)\\\\
&=\\sum_{k_1,k_2=-\\infty}^{\\infty}f\\left(k_1A^{-T}\\underline{e}_1+k_2A^{-T}\\underline{e}_2\\right)sinc(\\underline{y}\\cdot A\\underline{e}_1-k_1)sinc(\\underline{y}\\cdot A\\underline{e}_2-k_2) \\\\
 &\\qquad (please\\ review\\ linear\\ algebra)\\\\
&=\\sum_{k_1,k_2=-\\infty}^{\\infty}f\\left(k_1\\underline{u}^*_1+k_2\\underline{u}^*_2\\right)sinc(\\underline{y}\\cdot \\underline{u}_1-k_1)sinc(\\underline{y}\\cdot \\underline{u}_2-k_2) \\\\
&\\qquad \\begin{cases} \\underline{u}_1=A\\underline{e}_1 \\\\ \\underline{u}_2=A\\underline{e}_2 \\end{cases} \\quad \\begin{cases} \\underline{u}_1^*=A^{-T}\\underline{e}_1 \\\\ \\underline{u}_2^*=A^{-T}\\underline{e}_2 \\end{cases}\\\\
\\end{align*}$

 

用变量$\\underline{x}$来表示，有

$f(\\underline{x}) = \\displaystyle{ \\sum_{k_1,k_2=-\\infty}^{\\infty}f\\left(k_1\\underline{u}_1^*+k_2\\underline{u}_2^* \\right)sinc(\\underline{x}\\cdot\\underline{u}_1-k_1)sinc(\\underline{x}\\cdot\\underline{u}_2-k_2) } $

 $ \\begin{cases} \\underline{u}_1=A\\underline{e}_1 \\\\ \\underline{u}_2=A\\underline{e}_2 \\end{cases} \\quad \\begin{cases} \\underline{u}_1^*=A^{-T}\\underline{e}_1 \\\\ \\underline{u}_2^*=A^{-T}\\underline{e}_2 \\end{cases}$

该等式就是二维采样定理，若某二维函数的频谱受限于某平行四边形，该平行四边形基于$\\underline{u}_1,\\underline{u}_2$，那么在空域上的采样点晶格需要基于$\\underline{u}_1^*,\\underline{u}_2^*$