[离散时间信号处理学习笔记] 11. 连续时间信号的采样与重构

Posted 2020-10-23 TaigaComplex求职中

这一节主要讨论采样定理，在《傅里叶变换及其应用及其学习笔记》中有进行过推导与讲解，因此下面的内容也大同小异。不过如果是从《离散时间信号处理》这一本书的内容开始学习到这一节，则应先学习本文内容所需要的一些前置知识：傅里叶变换（连续时间），主要用到的是脉冲函数$\\delta$，以及周期脉冲函数Ш的傅里叶变换与相关性质。

比较重要的一点就是，本书采用的傅里叶变换是基于信号周期为$2\\pi$的假设，而《傅里叶变换及其应用及其学习笔记》中的假设为1，因此本书所采用的傅里叶变换公式有必要列出：

傅里叶变换：

$\\displaystyle{F(j\\Omega) =\\int_{-\\infty}^{\\infty}f(t)e^{-j\\Omega t}dt }$

傅里叶逆变换：

$\\displaystyle{f(t) = \\frac{1}{2\\pi}\\int_{-\\infty}^{\\infty}F(j\\Omega)e^{j\\Omega t}d\\Omega}$

 

此外，本文所用到的傅里叶变换卷积定理也有所不同：

$\\begin{align*}
\\mathcal{F}(f\\cdot g) &= \\frac{1}{2\\pi}F*G &
\\quad\\mathcal{F}^{-1}(F*G) &= 2\\pi f\\cdot g\\\\
\\mathcal{F}(f*g) &= F\\cdot G &
\\quad\\mathcal{F}^{-1}(F\\cdot G) &= f*g
\\end{align*}$

把前面的傅里叶变换公式代入容易证明上述卷积定理。

 

周期采样

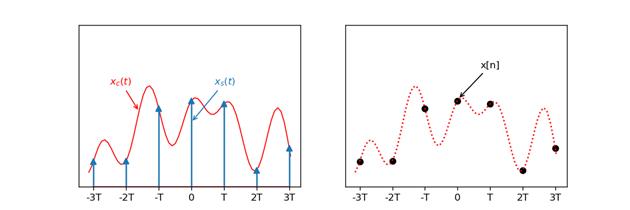
假设有连续信号$x_c(t)$，我们需要通过对该信号进行采样才能得到离散信号，即样本序列$x[n]$。连续信号与离散信号有以下关系：

$x[n] = x_c(nT),\\quad –\\infty<n<\\infty$

其中，$T$为采样周期（sampling period），它的倒数$f_s=\\frac{1}{T}$为采样频率（sampling frequency），即每秒的样本数。不过本书是用弧度/秒来表示频率，因此采样频率的是$\\Omega_s = \\frac{2\\pi}{T}$。这两种不同的采样频率表示方法是依赖于傅里叶变换的假设，一般分为周期为$1$以及$2\\pi$两种假设。

数学上是通过下面的式子来表示对连续信号的采样：

$\\displaystyle{x_s(t)=x_c(t)\\underbrace{\\sum_{n=-\\infty}^{\\infty}\\delta(t-nT)}_{sampling\\ function\\ s(t)=Ш_T}}$

其中的周期脉冲函数$Ш_T$就是周期为$T$的脉冲函数。利用脉冲函数$\\delta$的采样性质就能采集到一个函数相应位置的值。因此可以得到

$\\displaystyle{x_s(t)=\\sum_{n=-\\infty}^{\\infty}x_c(nT)\\delta(t-nT)}$

需要明确的一点是：$x_s(t)$是一个连续时间函数，取样点上的是脉冲，除了取样点之外的值为0；而$x[n]$是一个离散时间序列。

 

 

奈奎斯特采样定理

为了方便阅读，下面先列出了各个符号及其含义

Symbol	FT	DTFT	Info
$x_c(t)$	$X_c(j\\Omega)$	-	连续时间信号
$x[n]$	-	$X(e^{j\\omega})$	离散时间信号
$s(t)$	$S(j\\Omega)$	-	周期脉冲函数、即采样函数
$x_s(t)$	$X_s(j\\Omega)$	-	信号周期采样的数学表示
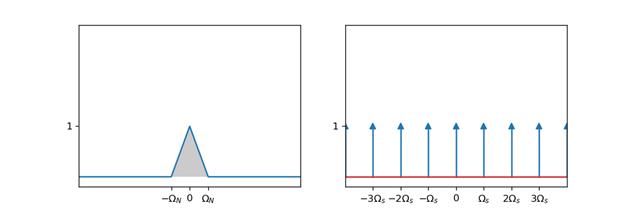
$\\Omega_N$	-	-	奈奎斯特频率，也就是带限信号的受限频率
$\\Omega_s$	-	-	采样频率
$T$	-	-	采样周期
$h_r(t)$	$H_r(j\\Omega)$	-	连续时间低通滤波器

 

周期脉冲函数$s(t) = Ш_T$的傅里叶变换仍然是一个周期脉冲函数（推导过程）

$S(j\\Omega) = \\frac{2\\pi}{T}Ш_{\\frac{2\\pi}{T}}$

那么根据傅里叶变换的卷积定理，可以得到$x_s(t)$的傅里叶变换如下

$\\begin{align*}
X_s(j\\Omega)
&= \\frac{1}{2\\pi}X_c(j\\Omega)*S(j\\Omega)\\\\
&= \\frac{1}{2\\pi}X_c(j\\Omega)*\\frac{2\\pi}{T}Ш_{\\frac{2\\pi}{T}}\\\\
&= \\frac{1}{T}X_c*Ш_{\\frac{2\\pi}{T}}
\\end{align*}$

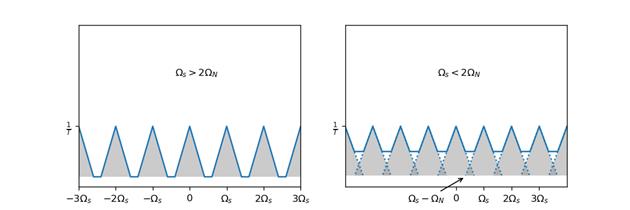
而脉冲函数的卷积又具有移位特性，那么$X_s(j\\Omega)$就相当于无数个经过移位的$\\frac{1}{T}X_c(j\\Omega)$的叠加。这种叠加能分为两种情况

• 如果原函数的傅里叶变换$X_c(j\\Omega)$的频率受限于$\\frac{\\Omega_s}{2} = \\frac{\\pi}{T}\\quad(\\Omega_s = \\frac{2\\pi}{T})$，那么$X_c(\\Omega)$经过移位后不会重叠。
• 否则原函数的傅里叶变换在经过移位后会重叠，这种情况被称为混叠（alias）。

如上面的四张图描述的是信号的频域。图1是一个频率受限于$(-\\Omega_N, \\Omega_N)$的信号，图2是一个在频域上周期为$\\Omega_s$的周期脉冲函数（从时域上看，该信号的频率为$\\Omega_s$），当信号与周期脉冲函数进行卷积后可以得到图3或者图4。

对于非混叠的频谱，我们能很容易地使用一个经过$T$加权（乘以$T$）的低通滤波器来得到原本的频谱，也就是说能通过该频谱还原原本的信号；不过对于混叠的频谱，采用低通滤波器得到的就不是原本的频谱，也就无法得到原本的信号了。

 

这意味着，对带限为$\\Omega_N$的信号进行采样，如果希望用采样后的样本恢复成原来的信号，那么采用频率$\\Omega_s$必须满足$\\Omega_s\\geqslant 2\\Omega_N$。这就是奈奎斯特采样定理（Nyquist-Shannon Sampling Theorem）。其中$\\Omega_N$被称为奈奎斯特频率（Nyquist frequency），$2\\Omega_N$被称为奈奎斯特率（Nyquist rate）。

 

 

由样本重构带限信号

按照上面的讨论，如果我们按照奈奎斯特采样定理对带限信号进行采样，那么就能用所得的样本重构原带限信号。

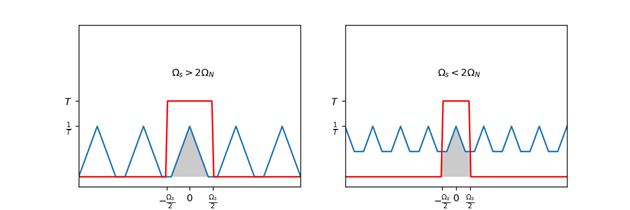
在上一小节的最后，我们可以看到如果我们遵循奈奎斯特采样定理，则能通过低通滤波器得到原信号的频谱，有了这个频谱，我们进行傅里叶逆变换则能得到原始信号，有以下推导过程：

$\\begin{align*}
x_c(t) &= \\mathcal{F}^{-1}(X_s(j\\Omega)H_r(j\\Omega)) \\qquad H_r(j\\Omega)=\\left\\{\\begin{matrix}
T, & |\\Omega|\\leqslant \\Omega_s/2=\\frac{\\pi}{T}\\\\
0, & else
\\end{matrix}\\right. \\\\
&= x_s(t)*h_r(t)\\qquad fourier\\ convolution\\ theorem\\\\
&= \\left\\{ \\sum_{n=-\\infty}^{\\infty}x[n]\\delta(t-nT)\\right \\}*\\left\\{ \\frac{sin(\\pi t/T)}{\\pi t/T} \\right\\}\\\\
&=  \\sum_{n=-\\infty}^{\\infty}x[n]\\left\\{\\delta(t-nT) * \\frac{sin(\\pi t/T)}{\\pi t/T} \\right\\}\\qquad x[n]\\ is\\ sample\\ value,constant \\\\
&= \\sum_{n=-\\infty}^{\\infty}x[n]\\frac{sin[\\pi (t-nT)/T]}{\\pi (t-nT)/T} \\qquad \\delta\\ shift\\ property
\\end{align*}$

因此，我们可以通过对采样$x[n]$进行上述运算以得到原始信号。

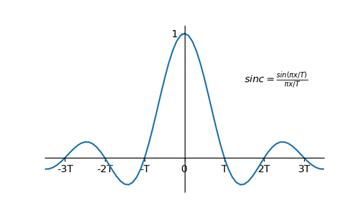
上面的式子可以分为两部分，一部分为采样值$x[n]$，另一部分为sinc函数，这个sinc函数就是低通滤波函数的时域模式，如下图是一个为$\\frac{sin(\\pi x/T)}{\\pi x/T}$的sinc函数。

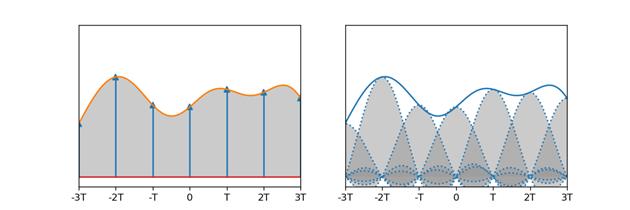
因此奈奎斯特采样定理也能这么理解：如果要采样的信号受限于$(-\\Omega_N, \\Omega_N)，$在采样频率$\\Omega_s$满足$\\Omega_s\\geqslant 2\\Omega_N$的前提下，采样得到的值为$x[n]$，通过对低通滤波器对应的sinc函数进行平移以及加权（乘以$x[n]$），然后把经过调整后的sinc函数进行叠加，即可得到原来的信号。

 

对照上面两幅图以及sinc函数的曲线，容易看出该函数在$\\pm T, \\pm 2T, \\pm 3T \\cdot\\cdot\\cdot$处的值都为0，而零点处的值为1，正是这个特点使得sinc函数的峰值就是采样点上的值。