求多个区间合并后区间大小的巧妙解决方法差分

Posted 2021-01-03 Roni

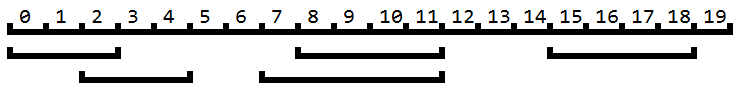
　　上图一共有5个区间，分别是[0,2]、[2,4]、[8,11]、[7,11]、[15,18]。如果要求这些区间合并后区间的大小，有两种简单的方法。

　　方法一：比较每两个区间的范围，如果两个区间有交集，则合并它们。最后所有区间会合并成几个离散的大区间，结果为这些区间大小之和。这种方法的时间复杂度是O(n^2)。

　　方法二：使用一个可以覆盖所有区间范围的数组，对每个区间进行标记，结果为数组中被标记元素的个数。这种方法的时间复杂度是O(nm)。

　　注：n是区间个数，m是所有区间总的范围。

 

　　如果n和m都比较大，那么上述两种方法的效率都不高。这里有一种很巧妙的解决这个问题的方法，它的时间复杂度是O(n+m)。使用一个可以覆盖所有区间范围的数组flg，初始化时将数组中的元素都置为0。对于每一个区间[l,r]，将flg[l]++，flg[r+1]--。最后使用一个累加器cnt，初始置为0。依次扫描数组中的每一个元素，对于第i个元素，cnt+=flg[i]。此时，若cnt>0，则说明i在某些区间中；若cnt==0，则证明i不在任何区间中。统计cnt>0的元素个数即可。

#include <cstdio>
#include <algorithm>
#include <iostream>
#include <string>
#include <cstring>
#include <vector>
#include <stack>
#include <queue>
#include <cmath>
#include <list>
#include <deque>
#include <map>
#include <set>
using namespace std;
#define ll long long
const double PI = acos(-1.0);
const int maxn = 101;
const int INF = 0x3f3f3f3f;
int dx[]={0,0,-1,1};
int dy[]={-1,1,0,0};

int n,m;
int f[maxn],cnt=0,sum=0;
struct node
{
    int l,r;
}a[maxn];
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=0;i<n;i++)
    {
        scanf("%d %d",&a[i].l,&a[i].r);
    }
    for(int i=0;i<n;i++)
    {
        f[a[i].l]++;
        f[a[i].r+1]--;
    }
    for(int i=0;i<m;i++)
    {
        sum+=f[i];
        if(sum>0)
            cnt++;
    }
    printf("%d
",cnt);
}