数字信号处理序列傅里叶变换 ( 傅里叶变换实例 | 傅里叶变换 | 傅里叶变换幅频特性 | 傅里叶变换相频特性 )
Posted 韩曙亮
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了数字信号处理序列傅里叶变换 ( 傅里叶变换实例 | 傅里叶变换 | 傅里叶变换幅频特性 | 傅里叶变换相频特性 )相关的知识,希望对你有一定的参考价值。
文章目录
一、序列傅里叶变换实例
求序列
x ( n ) = R N ( n ) ① x(n) = R_N(n) \\ \\ \\ \\ ① x(n)=RN(n) ①
的 序列傅里叶变换 SFT ;
1、傅里叶变换
傅里叶变换公式 : 根据 x ( n ) x(n) x(n) 序列 求 X ( e j ω ) 傅 里 叶 变 换 X(e^j\\omega) 傅里叶变换 X(ejω)傅里叶变换 ,
X ( e j ω ) = ∑ n = − ∞ + ∞ x ( n ) e − j ω n ② X(e^j\\omega) = \\sum_n=-\\infty^+\\infty x(n) e^-j \\omega n \\ \\ \\ \\ ② X(ejω)=n=−∞∑+∞x(n)e−jωn ②
将 ① 带入到 ② 傅里叶变换 公式中 , n n n 的取值范围是 [ 0 , N − 1 ] [0, N-1] [0,N−1] ,
X ( e j ω ) = ∑ n = − ∞ + ∞ x ( n ) e − j ω n = ∑ n = 0 N − 1 e − j ω n X(e^j\\omega) = \\sum_n=-\\infty^+\\infty x(n) e^-j \\omega n = \\sum_n=0^N-1 e^-j \\omega n X(ejω)=n=−∞∑+∞x(n)e−jωn=n=0∑N−1e−jωn
根据 " 等比级数求和 " 公式 , S n = a 1 + a 2 + a 3 + ⋯ + a n = a 1 ( 1 − q n ) 1 − q S_n = a_1+a_2+a_3+ \\cdots+a_n = \\cfraca_1 (1 - q^n)1 - q Sn=a1+a2+a3+⋯+an=1−qa1(1−qn) , ( 公比为 q ) , 一共有 N N N 项 ,
X ( e j ω ) = 1 − e − j ω n 1 − e − j ω X(e^j\\omega) = \\cfrac1-e^-j\\omega n1-e^-j\\omega X(ejω)=1−e−jω1−e−jωn
写成如下样式 , 是为了方便编程 ,
X ( e j ω ) = e − j ω N − 1 2 sin ( ω N 2 ) sin ( ω 2 ) X(e^j\\omega) = e^-j\\omega \\cfracN-12 \\cfrac \\sin( \\cfrac\\omega N2 ) \\sin( \\cfrac\\omega 2 ) X(ejω)=e−jω2N−1sin(2ω)sin(2ωN)
矩形窗序列 方便 计算机处理 , 将序列截断后只处理有限个序列比较容易 ,
将 信号 取一段数据 , 相当于 信号 乘以 矩形窗序列 ;
S F T [ R N ( n ) ] = N ω = 0 SFT[R_N(n)] = N \\ \\ \\ \\ \\omega = 0 SFT[RN(n)]=N ω=0
S F T [ R N ( n ) ] = 0 ω = 2 π k N , k = ± 1 , ± 2 , ⋯ SFT[R_N(n)] = 0 \\ \\ \\ \\ \\omega = \\cfrac2\\pi kN , k = \\pm1 , \\pm2 , \\cdots SFT[RN(n)]=0 ω=N2πk,k=±1,±2,⋯
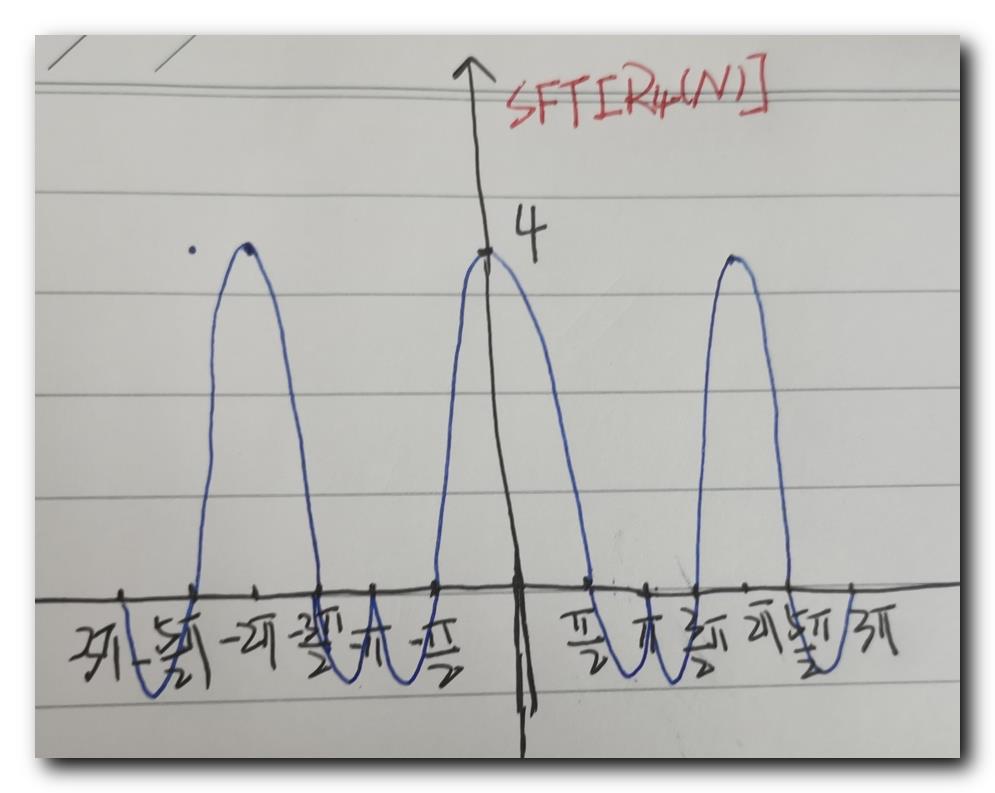
绘制 S F T [ R N ( n ) ] SFT[R_N(n)] SFT[RN(n)] 的坐标图 , 假设 N = 4 N = 4 N=4 ,
- 当 ω = 0 \\omega = 0 ω=0 时 , S F T [ R 4 ( n ) ] = 4 SFT[R_4(n)] = 4 SFT[R4(n)]=4
- 当 ω = 2 π k N = 2 π k 4 = π k 2 \\omega = \\cfrac2\\pi kN = \\cfrac2\\pi k4 = \\cfrac\\pi k2 ω=N2πk=42πk=2πk 时 , S F T [ R 4 ( n ) ] = 0 SFT[R_4(n)] = 0 SFT[R4(n)]=0 , 第一个点是 π 2 \\cfrac\\pi2 2π , 第二个点是 π \\pi π , 如下图所示 ;
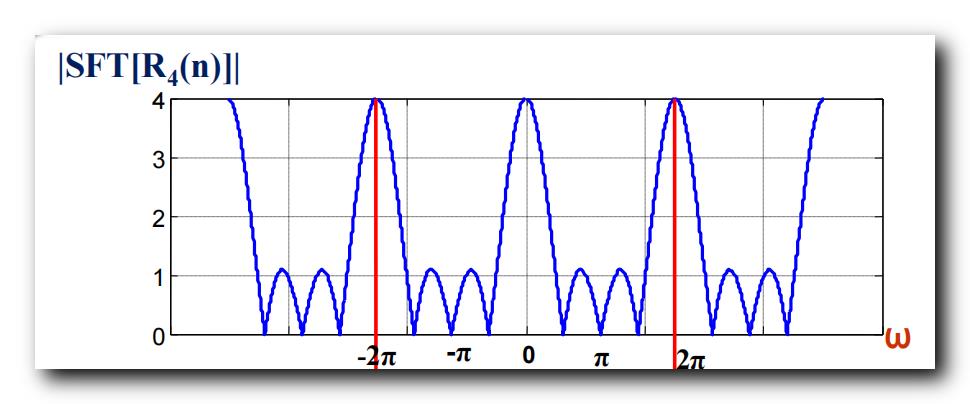
2、傅里叶变换幅频特性
幅频特性 : 在 matlab 中绘制效果如下 , matlab 中取模后再绘制 ;
3、傅里叶变换相频特性
相频特性 : matlab 中绘制其 相频特性 ,
相频特性 , 主要看 X ( e j ω ) = e − j ω N − 1 2 sin ( ω N 2 ) sin ( ω 2 ) X(e^j\\omega) = e^-j\\omega \\cfracN-12 \\cfrac \\sin( \\cfrac\\omega N2 ) \\sin( \\cfrac\\omega 2 ) X(ejω)=e−jω2数字信号处理序列傅里叶变换 ( 序列傅里叶变换与反变换 | 序列绝对可和 与 存在傅里叶变换之间的关系 | 序列傅里叶变换性质 )
数字信号处理傅里叶变换性质 ( 序列傅里叶变换共轭对称性质 | 序列实偶 傅里叶变换 实偶 | 序列实奇 傅里叶变换 虚奇 | 证明 “ 序列实奇 傅里叶变换 虚奇 “ )
数字信号处理序列傅里叶变换 ( 基本序列的傅里叶变换 | 单位脉冲序列 δ(n) 傅里叶变换 )
数字信号处理序列傅里叶变换 ( 基本序列的傅里叶变换 | 求 1 的傅里叶变换 )