动态规划经典例子——编辑距离问题

Posted 2020-11-16 texas

问题描述：

　　两个字符串，一个是起点字符串，另一个是终点。

　　例如，起点字符串ddl到终点字符串de的转换步骤如下：

　　ddl->del->def。

　　编辑距离为2。

算法分析：

　　首先考虑上面例子中ddl的第一个字符和def的第一个字符，它们是一样的，所以只需要计算a[2...lengthA]和b[2...lengthB]（dl和ef）之间的距离即可。

　　若两个字符串的第一个字符不同，例如adl和def，可以三选一：

• 把终点串的第一个字符插入到起点串的第一个字符之前（adl->dadl），然后计算a[1...lengthA]和b[2...lengthB]（dadl和def）的距离即可；
• 删除起点串的第一个字符（adl->dl），然后计算a[2...lengthA]和b[1...lengthB]（dl->def）的距离即可；
• 修改起点串的第一个字符成终点串的第一个字符（adl->ddl），然后计算a[2...lengthA]和b[2...lengthB]（dl和ef）的距离即可。

　　考虑起点串的第i个字符和终点串的第j个字符的话也是一样的。

当不考虑起点串的前i-1字符和终点串的前j-1个字符，如果起点串的第i个字符和终点串的第j个字符相等，即a[i-1] = b[j-1]，则只需要计算a[i...lengthA]和b[j...lengthB]之间的距离即可。

　　如果不相等，可以三选一：

• 把终点串的第j个字符插入到起点串的第i个字符之前，然后计算a[i...lengthA]和b[j+1...lengthB]的距离即可；
• 删除起点串的第i个字符，然后计算a[i+1...lengthA]和b[j...lengthB]的距离即可；
• 修改起点串的第i个字符成终点串的第j个字符，之然后计算a[i+1...lengthA]和b[j+1...lengthB]的距离即可；

  　  那么进行三选一的依据是什么呢？是起点串的前i-1字符和终点串的前j-1个字符的编辑距离。

　　递归方程：

 

 

 

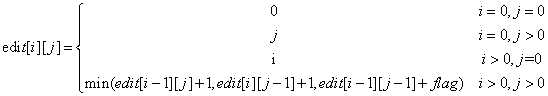
　　edit[i-1][j]+1相当于给起点串的最后插入了终点串的最后的字符，插入操作使得edit+1，之后计算edit[i-1][j]；

　　edit[i][j-1]+1相当于将起点串的最后字符删除，删除操作edit+1，之后计算edit[i][j-1];

　　edit[i-1][j-1]+flag相当于通过将起点串的最后一个字符替换为终点串的最后一个字符。若a[i-1] = b[j-1]，flag = 0；若a[i-1] != b[j-1]，flag = 1。

　　

#include<iostream>
#include<string.h>
using namespace std;


int main() {
    char a[2000], b[2000];

    cin.getline((a+1), 2001);
    cin.getline((b+1), 2001);
    
    int lengthA = strlen(a) - 1;
    int lengthB = strlen(b) - 1 ;
    
    int editDistance[2001][2001];
    editDistance[0][0] = 0;
    
    for(int i = 1; i <= lengthA; i++) {
        editDistance[i][0] = i;
    }
    for(int i = 1; i <= lengthB; i++) {
        editDistance[0][i] = i;
    }
    for(int i = 1; i <= lengthA; i++)
        for(int j = 1; j <= lengthB; j++) {
            if(a[i] == b[j]) {
                editDistance[i][j] = editDistance[i-1][j-1];
            }
            else {
                editDistance[i][j] = min(editDistance[i-1][j], min(editDistance[i][j-1], editDistance[i-1][j-1])) + 1;
            }
        }
    
    cout << editDistance[lengthA][lengthB];
    
    return 0;
}

View Code

复杂度分析

　　时间复杂度：O（m*n）

　　空间复杂度：O（1）

心得

递归方程很重要。