经典动态规划：编辑距离

Posted 2021-04-18 面向大象编程

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了经典动态规划：编辑距离相关的知识，希望对你有一定的参考价值。

本期例题：LeetCode 72. Edit Distance 编辑距离（Hard）

给定字符串 s 和 t，将 s 转换成 t。你可以进行三种操作：插入一个字符、删除一个字符、替换一个字符。计算将 s 将转换成 t 的最小操作数。

示例：
输入：word1 = "horse", word2 = "ros"
输出：3
解释：
    horse -> rorse (将 'h' 替换为 'r')
    rorse -> rose (删除 'r')
    rose -> ros (删除 'e')

今天我们要讨论一道经典的二维动态规划问题：编辑距离（Edit Distance）。

你可能在各种地方都听说过「编辑距离」。编辑距离又叫莱文斯坦距离（Levenshtein distance），用于评估两个字符串的差异程度，在拼写检查、文本对比（diff）等场景中都有应用。编辑距离问题的实际意义使得它非常受面试官青睐。

编辑距离问题是 LeetCode Hard 题目，很多同学做这道题的时候会觉得很难，总是找不到思路。这道题的难点主要有两个：

第一，如何在拿到题目的时候想到可以用动态规划来解。这一般需要你做过二维动态规划的经典例题，然后联想到本题的思路。
第二，如何从题目描述中拆解出动态规划的具体思路。这需要你有一些拆解动态规划题目的技巧。

今天的文章会以编辑距离问题为例，讨论如何攻克动态规划问题的这两个难点。我们先讲讲如何从复杂的问题中拆解出动态规划的思路，再讲讲如何在动态规划题目之间进行联想。

编辑距离的拆解思路

假设你已经知道了编辑距离这道题是用动态规划来做，那怎么能进一步得出具体的思路呢？

动态规划题目的解题步骤我们都知道，要先定义子问题，再写出子问题的递推关系。道理我们都懂，但是对于具体的题目，如何定义子问题和子问题的递推关系还是很需要技巧的。

如果直接从整体看编辑距离，其实很难下手。究竟怎样组合插入、删除、替换操作，才能得到最少的编辑次数呢？这些操作之间又满足怎样的性质呢？

在做动态规划问题的时候，如果你觉得从全局考虑很困难，就试试先不考虑全局，从局部入手。我们可以只考虑其中的「一步」，至于剩下的步骤，就交给其他子问题完成就行。对于编辑距离来说，这「一步」就是指「单次的编辑操作」。

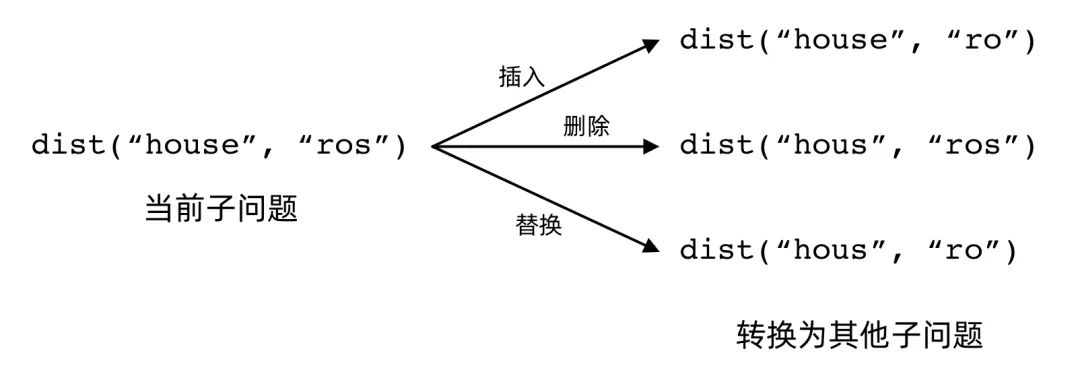
我们以 "horse" 和 "ros" 为例。我们考虑这「一步」做的是插入、删除还是替换操作。

如果做插入操作，那么插入的是 "ros" 末尾的 's'，我们还需要计算 "horse" 到 "ro" 的编辑距离；
如果做删除操作，那么删除的是 "horse" 末尾的 'e'，我们还需要计算 "hors" 到 "ros" 的编辑距离；
如果做替换操作，那么是把 "horse" 末尾的 'e' 替换为 "ros" 末尾的 's'，我们还需要计算 "hors" 到 "ro" 的编辑距离。

三种不同的编辑操作

为什么要关注「一步」呢？因为动态规划最关键的地方在于寻找「子问题的递推关系」，或者叫「状态转移方程」。所谓「递推关系」，就是一个子问题经过怎样的「一步」操作可以转换为另一个子问题。

例如，之前讲过的打家劫舍问题，计算子问题的时候，我们可以有两种选择：由计算而来，或者由计算而来。也就是说，子问题可以转换为或。

这有点类似递归的思路。我只需要把当前这一步计算做好，然后相信递归函数能帮我做好剩下的计算。动态规划其实很像递归，只不过动态规划一般是自底向上计算，保存每个子问题。

对于编辑距离问题，我们的「一步」有三种「选择」。选择插入、删除或者替换操作，我们可以将当前子问题转换为不同的子问题：

这样，编辑距离的子问题如何定义其实就相当清楚了。不同的子问题其实就是 s 和 t 有不同的长度。我们可以定义子问题为「s[0..i) 和 t[0..j) 的编辑距离」。子问题的递推关系就有三个分支，分别对应插入、删除、替换三种操作。

这样，我们就有了动态规划解法的基本思路，接下来，我们继续套用动态规划的「解题四步骤」，来给出完整的题解吧。

套用解题四步骤

老规矩，我们使用动态规划的解题四步骤来写出题解代码。

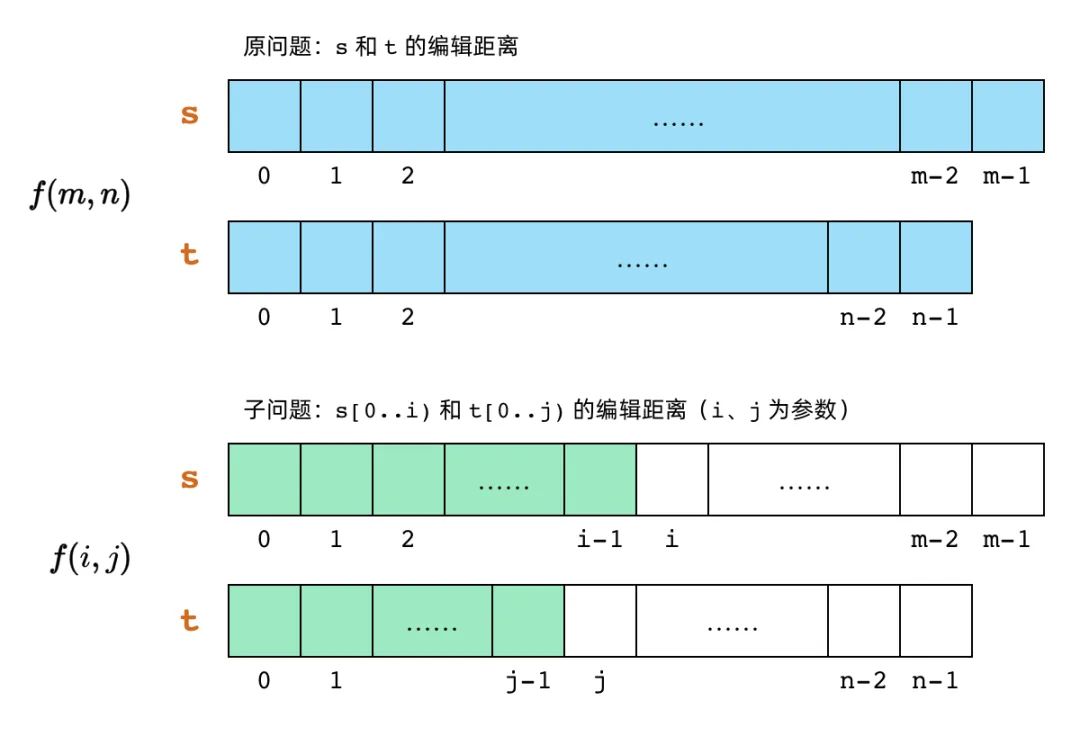
步骤一：定义子问题

上文我们已经讨论了两个字符串的动态规划问题的子问题套路。和最长公共子序列问题一样，我们可以定义子问题为「s[0..i) 和 t[0..j) 的编辑距离」。那么，这是一道二维动态规划问题。

步骤二：写出子问题的递推关系

子问题的递推关系就和三种编辑操作相对应。对于 s[0..i) 和 t[0..j) 的编辑距离，我们有三种方案：

删除 s[i-1]，然后计算 s[0..i-1) 和 t[0..j) 的编辑距离
插入 t[j-1]，然后计算 s[0..i) 和 t[0..j-1) 的编辑距离
将 s[i-1] 替换为 t[j-1]，然后计算 s[0..i-1) 和 t[0..j-1) 的编辑距离

对于这三种方案，我们需要找出其中操作最少的方案。用公式写出来的话，就是：

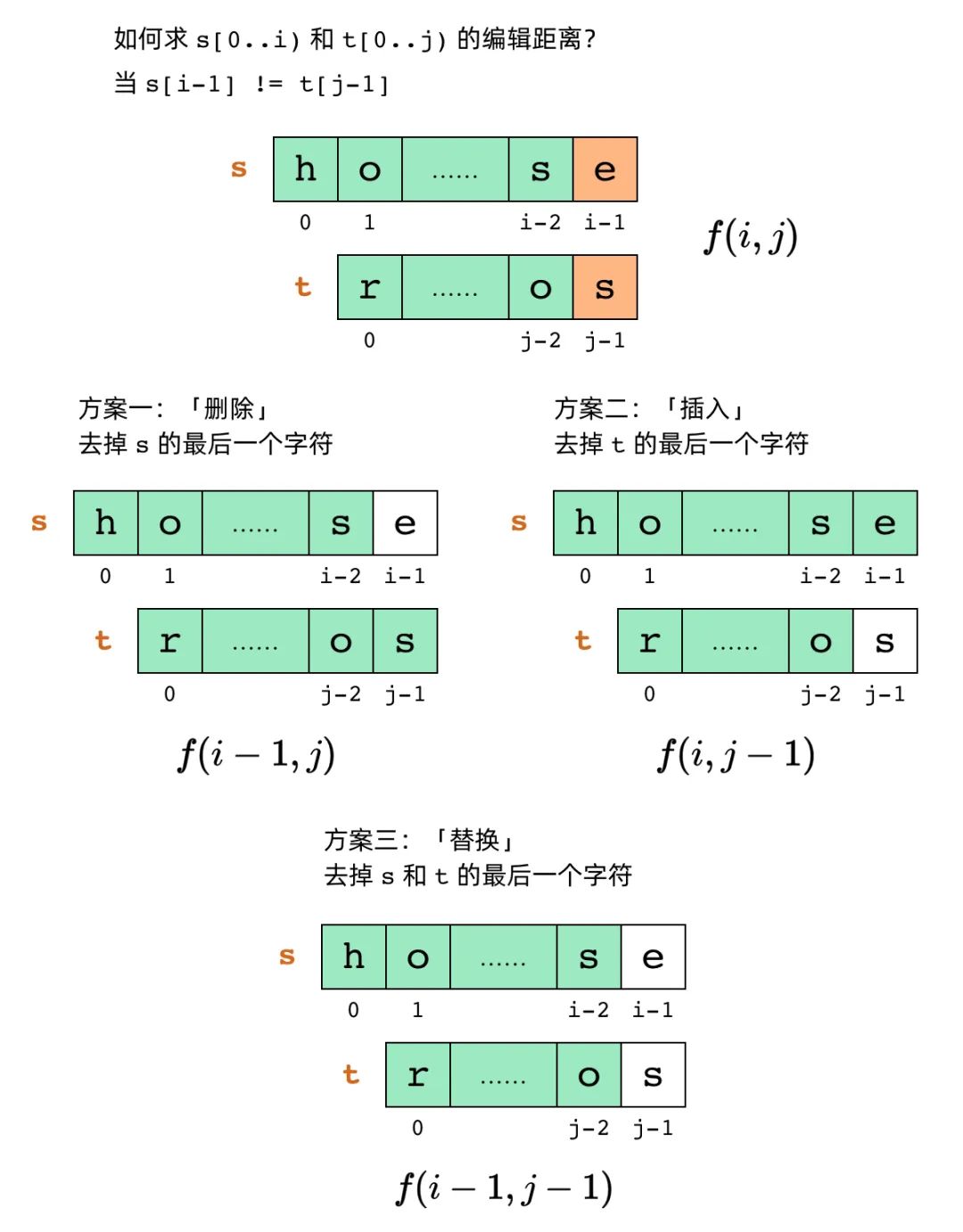
需要注意的是，上面的「替换」方案，如果 s[i-1] 和 t[j-1] 本来就相等的话，是不需要这一步替换的，编辑操作可以减少一次。那么，我们要比较 s[0..i) 和 t[0..j) 的最后一个字符，即 s[i-1] 和 t[j-1]。这可能会有两种情况：

第一种情况：如果 s[i-1] != t[j-1]，我们可以做「插入」、「删除」或者「替换」操作。

第二种情况：如果 s[i-1] == t[j-1]，那么这最后一个字符不需要进行任何编辑操作，我们可以去掉最后一个字符，然后计算 s[0..i-1) 和 t[0..j-1) 的编辑距离。用公式写出来的话，就是：

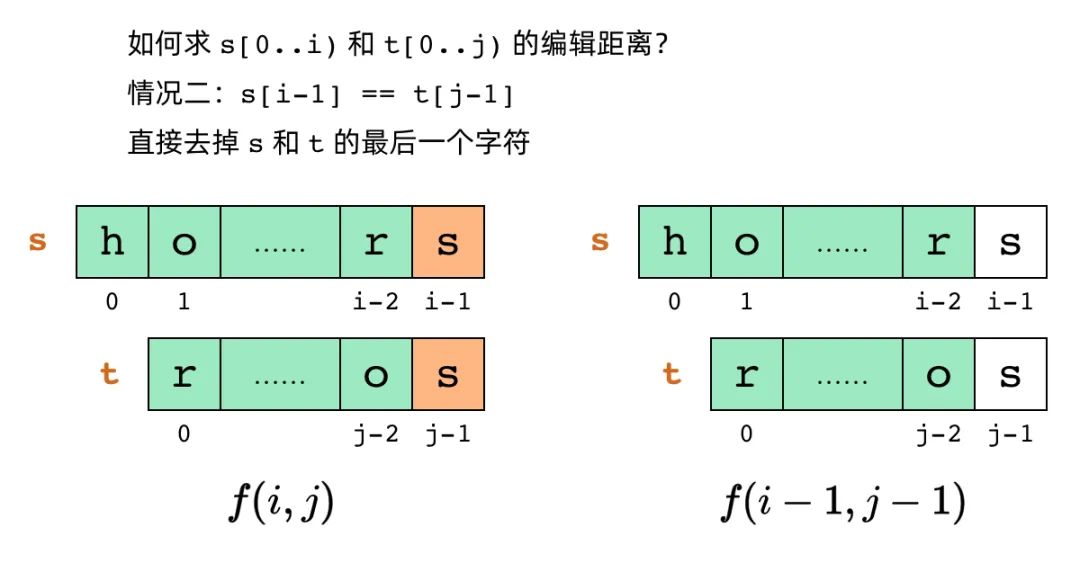
这样，我们得到最终的子问题递推关系为：

另外，别忘了递推关系的 base case。

当时， s[0..i) 为空，还剩 t[0..j) 的个字符，我们需要做次插入操作，因此。
当时，类似地，有。

步骤三：确定 DP 数组的计算顺序

对于二维动态规划问题，我们需要定义二维的 DP 数组，其中 dp[i][j] 对应子问题，即 s[0..i) 和 t[0..j) 的编辑距离。

设 s 的长度为，t 的长度为，则、的取值范围分别为：。DP 数组是一个的矩形。

为了确定 DP 数组的计算顺序，我们需要知道子问题的依赖方向。观察子问题的递推关系，依赖于、和，我们在 DP 数组中画出依赖方向的箭头：

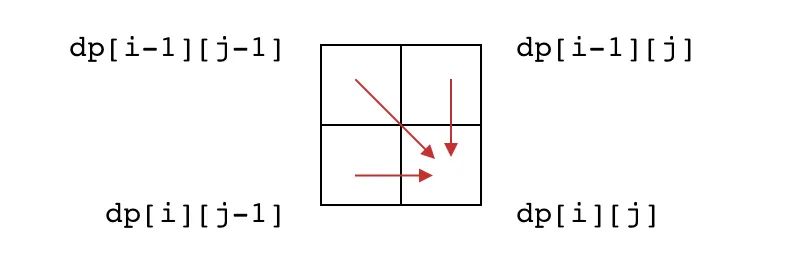
我们发现，编辑距离问题的子问题依赖方向和最长公共子序列问题一模一样！这是因为，在两道题目中，都依赖于、和。虽然具体的递推关系不一样，但是只要是这样的依赖关系，DP 数组的计算顺序就是一样的。

那么，编辑距离问题，DP 数组的计算顺序同样是从左到右、从上到下。我们应该以这样的顺序遍历 DP 数组：

for (int i = 0; i <= m; i++) {
    for (int j = 0; j <= n; j++) {
        // 计算 dp[i][j] ...
    }
}

最终我们得到的题解代码为：

public int minDistance(String s, String t) {
    // 子问题：
    // f(i, j) = s[0..i) 和 t[0..j) 的编辑距离

    // f(0, j) = j
    // f(i, 0) = i
    // f(i, j) = f(i-1, j-1), if s[i-1] == t[j-1]
    //           max: f(i-1, j) + 1
    //                f(i, j-1) + 1
    //                f(i-1, j-1) + 1, if s[i-1] != t[j-1]

    int m = s.length();
    int n = t.length();
    int[][] dp = new int[m+1][n+1];
    for (int i = 0; i <= m; i++) {
        for (int j = 0; j <= n; j++) {
            if (i == 0) {
                dp[i][j] = j;
            } else if (j == 0) {
                dp[i][j] = i;
            } else {
                if (s.charAt(i-1) == t.charAt(j-1)) {
                    dp[i][j] = dp[i-1][j-1];
                } else {
                    dp[i][j] = 1 + min3(
                        dp[i-1][j],  // 删除操作
                        dp[i][j-1],  // 插入操作
                        dp[i-1][j-1] // 替换操作
                    );
                }
            }
        }
    }
    return dp[m][n];
}

private int min3(int x, int y, int z) {
    return Math.min(x, Math.min(y, z));
}