简言翻译记忆的原理：用动态规划算法求解最短编辑距离

Posted 2021-04-18 简言

在上一篇文章（）中，我用一个英文单词听写改错的例子给大家简单介绍了什么是两个英文单词之间的“最短编辑距离”。但在上面案例中我们只是纯用肉眼来辨识两个单词之间的编辑距离，在这篇文章中我将介绍如何使用动态规划（Dynamic Programming）算法来计算两个单词之间的最短编辑距离。

首先我们来看几个小例子：

例一

设：

“fxy”和“fab”之间的编辑距离是N；

“fxyb”和“fab”之间的编辑距离是M1；

“fx”和“fab”之间的编辑距离是M2；

“fx”和“fa”之间的编辑距离是M3；

问：N和M1、M2和M3之间的关系分别是什么？

我们使用下面这个网站来进行计算：

https://planetcalc.com/1721/

通过计算可知：

N=2

M1=2

M2=2

M3=1

大家仔细看N和M1的值，发现他们都是2，但去看例子的内容却发现难以理解，从“fxyb”到“fxy”明明增加了一个b，但这两个字符串分别与fab去进行编辑距离计算时，得到的结果竟然是一样的，都是2。

不仅如此，从“fxy”到“fx”明明减少了一个y，但这两个字符串分别与fab去进行编辑距离计算时，得到的结果竟然也是一样的，也都是2。

在思考这个问题时，我们首先应该明确的是：我们绝对不能用字符串的长短来判断编辑距离，因为编辑距离探讨的是一个字符串通过怎样的操作能够变成另一个字符串。

那我们判断编辑距离时要看什么呢？显然是字符串中的每一个字符。

从fxy到fab，因为第一个字符f是一样的，所以只需要将x替换成a，将y替换成b，通过两步操作即可实现转换，因此编辑距离是2。

从fxyb到fab，因为两边的字符f和b都是一样的，所以只需要将x替换成a，将y删掉，通过两步操作即可实现转换，因此编辑距离还是2。

从fx到fab，因为第一个字符f是一样的，所以只需要将x替换成a，再增加一个b，通过两步操作即可实现转换，因此编辑距离也是2。

例二：

设：

“a”和“bm”之间的编辑距离是N；

“am”和“bm”之间的编辑距离是M1；

“an”和“bm”之间的编辑距离是M2。

问：N和M1、M2之间的关系分别是什么？

我们初看到这个问题时会这样想：如果“a”和“bm”之间的编辑距离是N，我们又在a后新加了一个字母m，变成am，那么在计算am和bm之间的编辑距离M1时，肯定是多加一步呀：N+1=M1。

同样的，我们在a后新加了一个字母n，变成an，那么在计算an和bm之间的编辑距离M2时，也是多加了一个字母，所以N+1=M2.

然而，我们算一下，在这个例子中，“a”和“bm”的编辑距离应该为2：

“a”和“bm”之间的编辑距离

“am”和“bm”的编辑距离应该为“1”：

“am”和“bm”之间的编辑距离

“an”和“bm”之间的编辑距离

所以：N=2，M1=1，M2=2。

结果是：

N-1=2-1=M1，而非之前我们以为的N+1=M1。

N+0=2+0=M2，而非之间我们认为的N+1=M2.

为什么会发生这种情况呢？

大家仔细看这个问题，我们在第一步多加的那个字母m并非任意字母，而是“bm”的第二个字母。一旦我们加了这个字母，实质上是减少了编辑工作量，缩短了编辑距离。

我们在第二步多加的那个字母n是bm中都没有的字母。一旦我们加了这个字母使得an和bm的长度相等，原来从a到bm需要花费“一步替换（a->b）”和“一步新增（+m）”，总共是两步；现在则需要花费“两步替换”（a->b和n->m），所以编辑距离还是2。

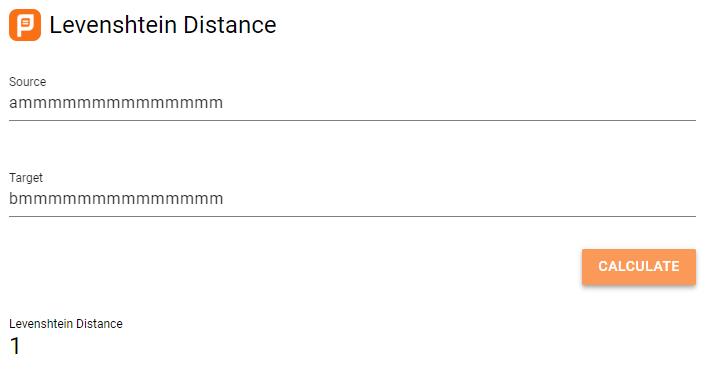
因此，还是那句话，大家千万不要用两个单词的长度来判断编辑距离的长短，不能因为单词长了，编辑距离就也跟着提高了。如：

ammmmmmmmmmmmmm

和

bmmmmmmmmmmmmmm

之间的编辑距离也是1，如下图：

例三：

设：

“abc”和“bcm”之间的编辑距离是N；

“ab”和“bcm”之间的编辑距离是M；

问：N和M之间的关系是什么？

我们看到这个问题后，会有这样的想法：“abc”和“bcm”之间的编辑距离是N，现在我删了一个c，那么肯定是：N-1=M，即：N=M+1。

我们来算一下，在这个例子中，“abc”和“bcm”的编辑距离应该为2，“ab”和“bcm”的编辑距离应该为“3”，所以：N=2，M=3，结果是：N+1=M，即：N=M-1。

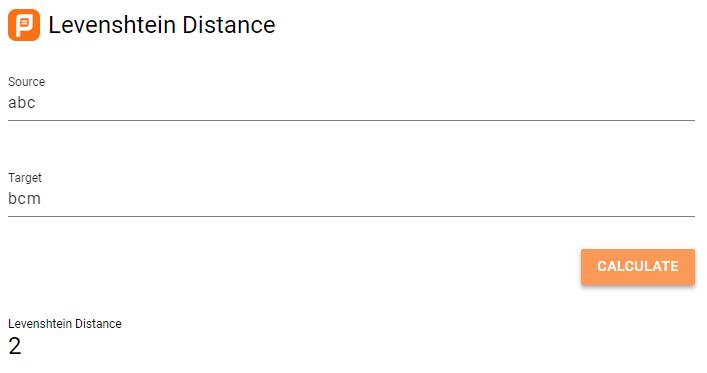
“abc”和“bcm”之间的编辑距离

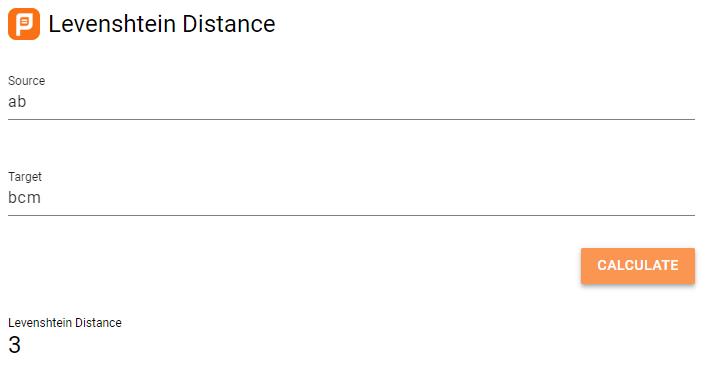
“ab”和“bcm”之间的编辑距离

如果跟着感觉走，我们又会算错。

仔细观察会发现，“abc”和“bcm”两个字符串中都有bc，所以这两个字符串之间转换时最方便的操作是：删除一个a，再新增一个b，一共是两步。

而“ab”和“bcm”则只有“b”是一样的，我们在转换时需要：删除一个a、新增一个c和新增一个m，编辑距离变成了3。

如此一看，删了的那个c反而是“帮了倒忙”，把人家“bc”活生生给拆散了。

例四：

我们之前比较的是INTENTION和EXECUTION这两个单词之间的编辑距离，你我可能都认识这两个单词，但是下面的这两个单词你看看你是否也认识：

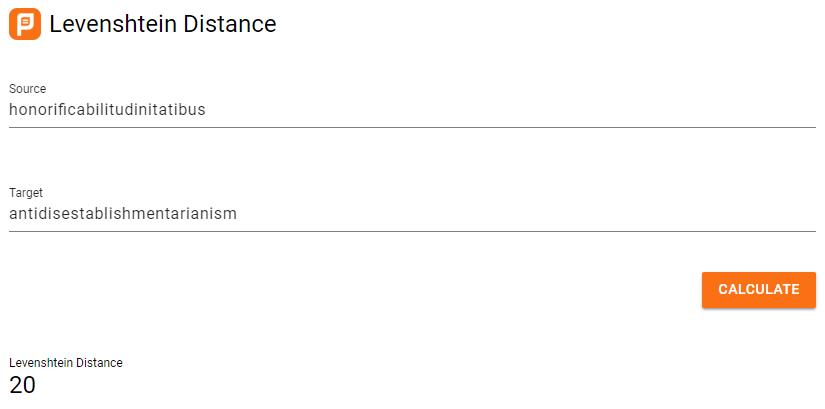
honorificabilitudinitatibus

antidisestablishmentarianism

估计绝大大大大多数的朋友都不认识这两个单词。当然，我也不认识，这是网上流传的“十个超级长的英语单词”之二，在写这篇帖子之间我也没见过。

第一个单词一共有27个字母，第二个单词一共有28个字母。

如果把这两个单词输入到上一篇帖子中我分享的编辑距离计算网站，得到的结果是：20。

那么这两个单词之间的“最短编辑距离”是如何计算出来的呢？这回我们用肉眼看可没有那么容易看出来了。

为了能够将这两个单词的最短编辑距离用计算机算出来，我们还得给大家简单分享一种我认为比较好理解的计算方法。

根据前面的几个例子，我们知道在判断两个字符串之间的编辑距离时不能看字符串的长短，而是应该看“内涵”。

首先，我们看看“fxyb”和“fab”以及“am”和“bm”这种情况，两组词的最后一个字符都相同，分别是b和m，所以：

“fxyb”和““fab”之间的距离 等于 “fxy”和“fa”之间的距离。

“am”和“bm”之间距离 等于 “a”和“b”之间的距离。

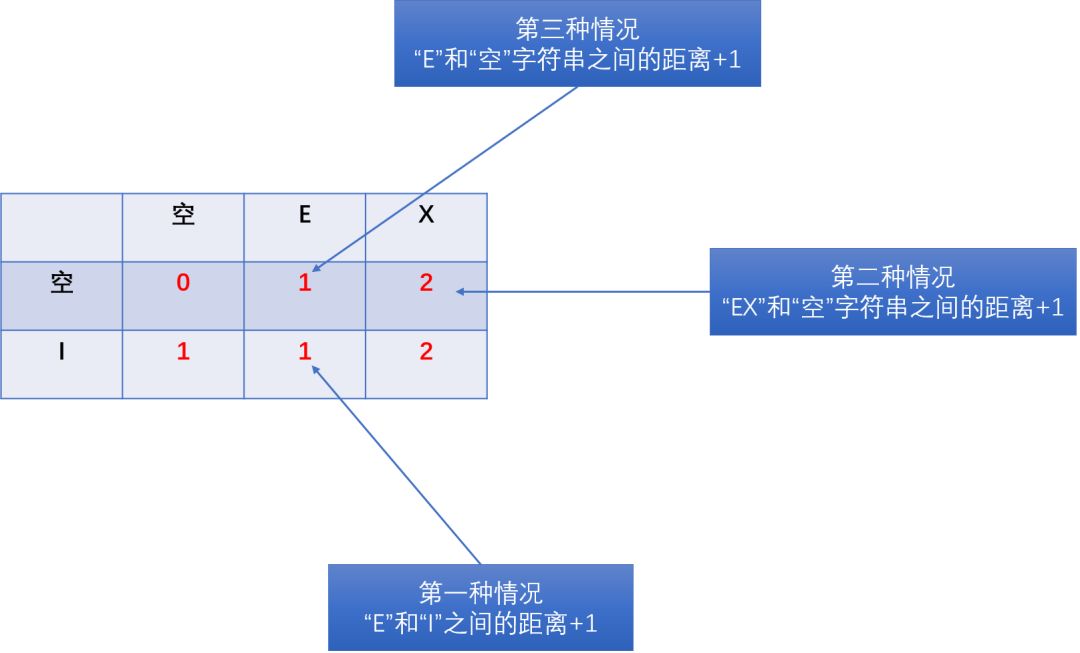
而在计算“fxy”和“fab”之间的距离时，由于两个字符串的最后一个字符不一样，所以就有这三种情况：

第一种情况：

“fxy”和“fab”的距离等于“fx”和“fab”的距离+1。

如下图所示：

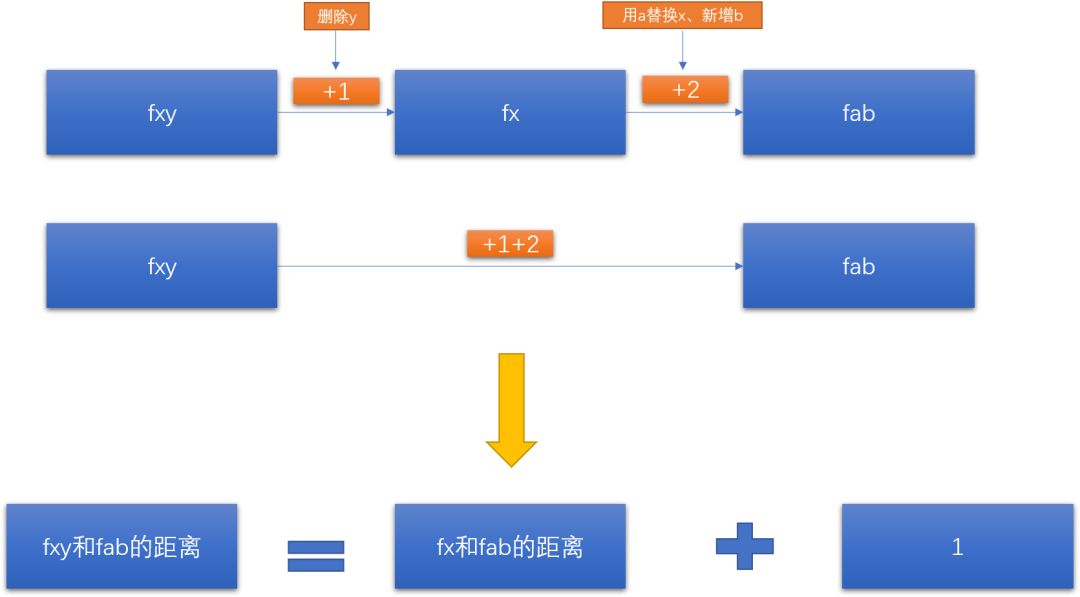
理解起来就是：从fxy到fx转换时删除了1个y，相当于用了1步，而fx和fab的距离是2（第一步是用a替换x，第二步是新增一个b），所以fxy到fab的编辑距离变成了3，相当于“fx”和“fab”的距离（2）+1。

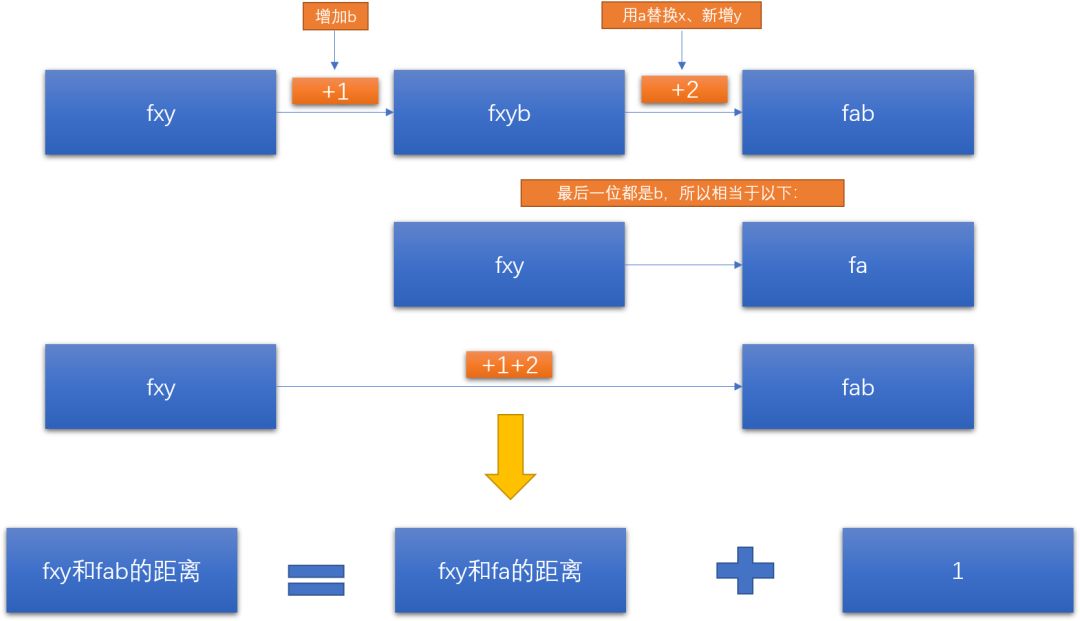
第二种情况：

现在“fxy”和“fab”的最后一位虽然不一样，但是我们可以通过在“fxy”后面加一个“b”，使之变成“fxyb”，此时我们计算一下“fxyb”和“fab”的距离，这个距离就等于“fxy”和“fa”的距离。

所以“fxy”和“fab”的距离=“fxy”和“fa”的距离+1。

如下图所示：

第三种情况：现在“fxy”和“fab”的最后一位不一样，但是我们可以通过把“fxy”后面的y替换成一个“b”，使之变成“fxb”。

如下图所示：

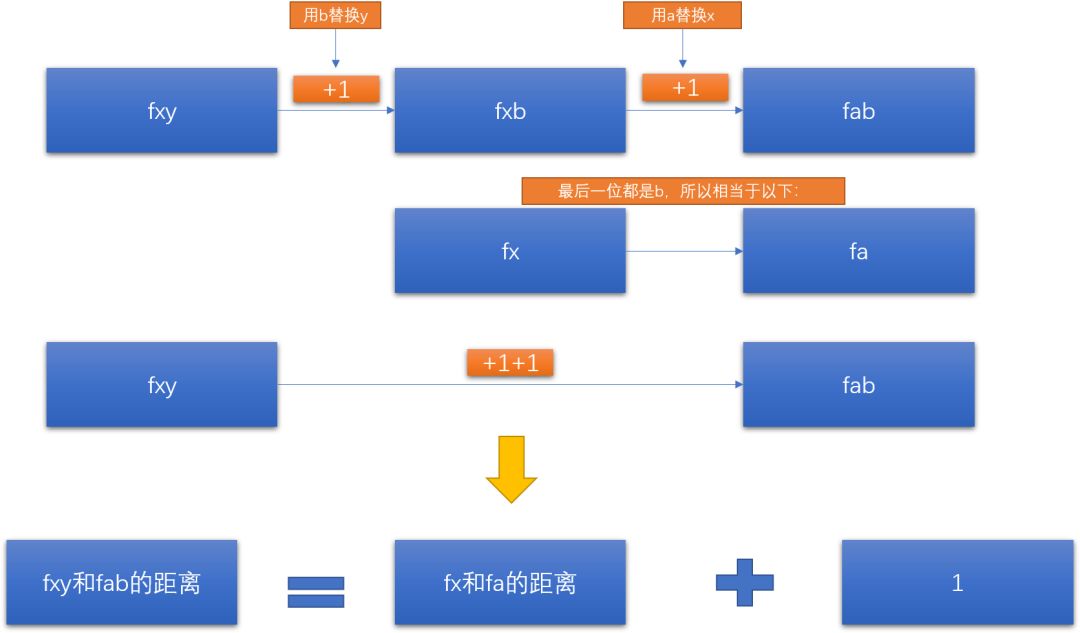
上图这样来理解：从fxy到fxb，我们用b替换了y，这时候用了一步；然后从fxb到fab，我们用a替换了x，又用了一步，所以一共用了两步。

而fxb到fab的距离相当于fx到fa的距离。

所以：fxy和fab的距离相当于fx和fa的距离+1。

我们现在仔细分析一下上面三种方法，发现三种方法分别计算出来了一个编辑距离：

以上三个编辑距离中，最短的编辑距离是：2。

所以：fxy和fab之间的最短编辑距离是：2。

大家看到这里，可能终于明白了“编辑距离”和“最短编辑距离”的区别。

对于第一次接触“最短编辑距离”的人来说，最容易搞混的就是：“编辑距离”和“最短编辑距离”的区别，正所谓：

距离好几条

最短要盯牢

随便算一算

不一定最小

从一个字符串到另一个字符串可以有很多种转换的方法，但是距离有长有短，我们在计算两个字符串的编辑距离时更在乎的是最短的编辑距离。

既然上面的方法对于fxy和fab这两个字符串都有用，那么对于任何两个字符串我们都可以采取上面的方法，遇到长字符串时，我们只需要逐层的往下去算，直到字符串不能缩短为止。

下面，我们以INTENTION和EXECUTION这两个单词为例。

第一步：

由于这两个单词的最后四位字符都一样，所以：

INTENTION和EXECUTION的距离等于INTEN和EXECU的距离。

第二步：

由于INTEN和EXECU这两个单词的最后一位不一样，所以我们要考虑三种情况：

第一种：

INTE和EXECU的距离+1（即：前面的字符串少一位）

第二种：

INTEN和EXEC的距离+1（即：后面的字符串少一位）

第三种：

INTE和EXEC的距离+1（即：两个字符串各少一位）

对于以上三种的每一种情况，我们又可以分成几个小问题，如：

第一种：

    INTE和EXECU的最后一位不一样，所以分为三种情况：

        第一种：INT和EXECU的距离+1

        第二种：INTE和EXEC的距离+1

        第三种：INT和EXEC的距离+1

第二种：

    INTEN和EXEC的最后一位不一样，所以分为三种情况：

        第一种：INTE和EXEC的距离+1

        第二种：INTEN和EXE的距离+1

        第三种：INTE和EXE的距离+1

第三种：

    INTE和EXEC的最后一位不一样，所以分为三种情况：

        第一种：INT和EXEC的距离+1

        第二种：INTE和EXE的距离+1

        第三种：INT和EXE的距离+1

......

写到这儿，似乎再写下去就又要写出好多来。但是，大家如果仔细思考，就会发现，我们把一个大的问题（求INTENTION和EXECUTION的距离）分解成了一个个的小问题或子问题，只要求得了子问题的结果，就能逐层往回算获得大的问题的结果。

这种方法叫做：动态规划（Dynamic Programming）。

为了解决上面的问题，我们更倾向于从最小的问题开始来求解，我们来画下面一个矩阵：

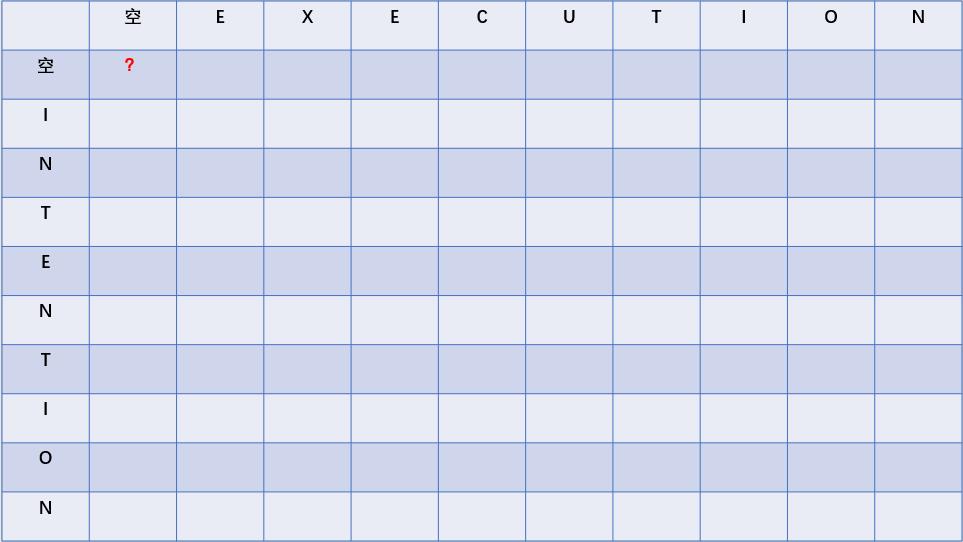
我们把两个单词分别放到这个矩阵的横轴和数轴方向。上图的问号处代表的是“空”字符串和“空字符串”之间的编辑距离，显然这个应该是0，所以，我们把0填进去，如下图：

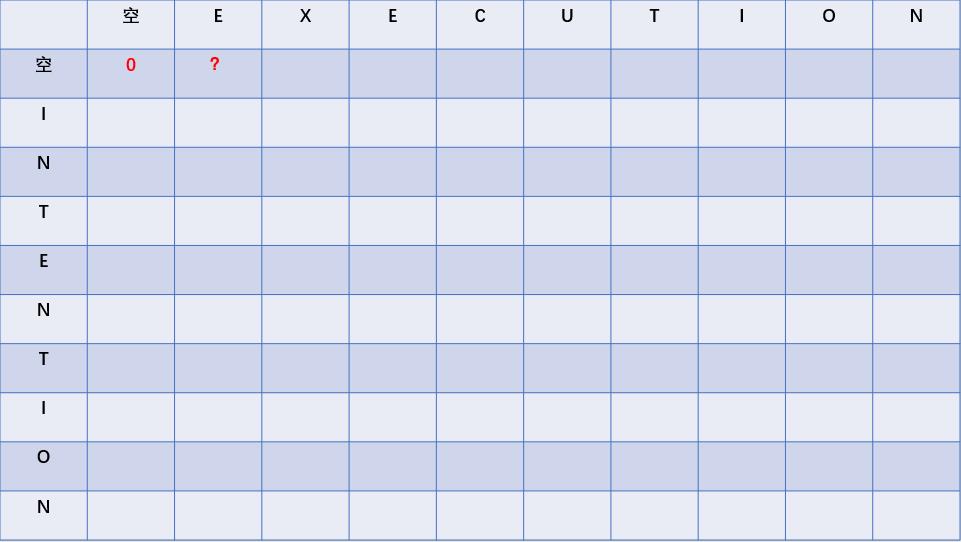
上图的问号处代表的是“空”字符串和“E”之间的距离，这个距离显然是1，所以把1填进去，如下图：

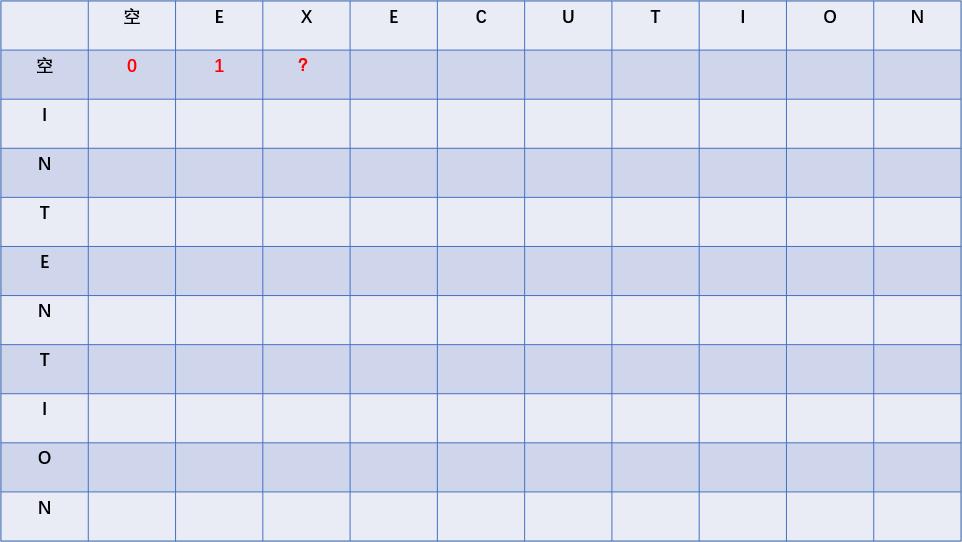
上图的问号处代表的是“空字符串”和“EX”之间的距离，这个距离显然是2，所以我们把2填进去，如下图：

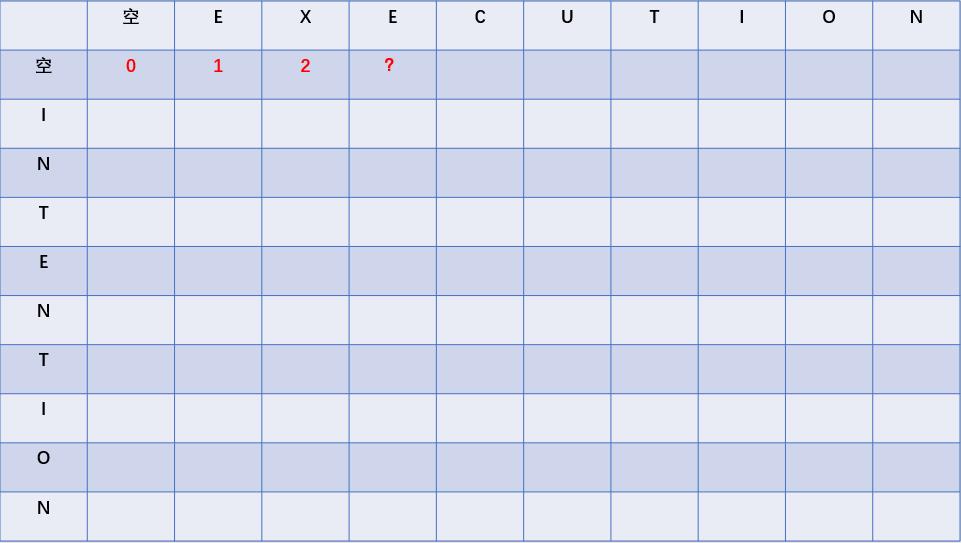
上图的问号处代表的是“空”字符串和“EXE”之间的距离，这个距离显然是3。以此类推，我们可以把第一排都填好对应的距离，如下图：

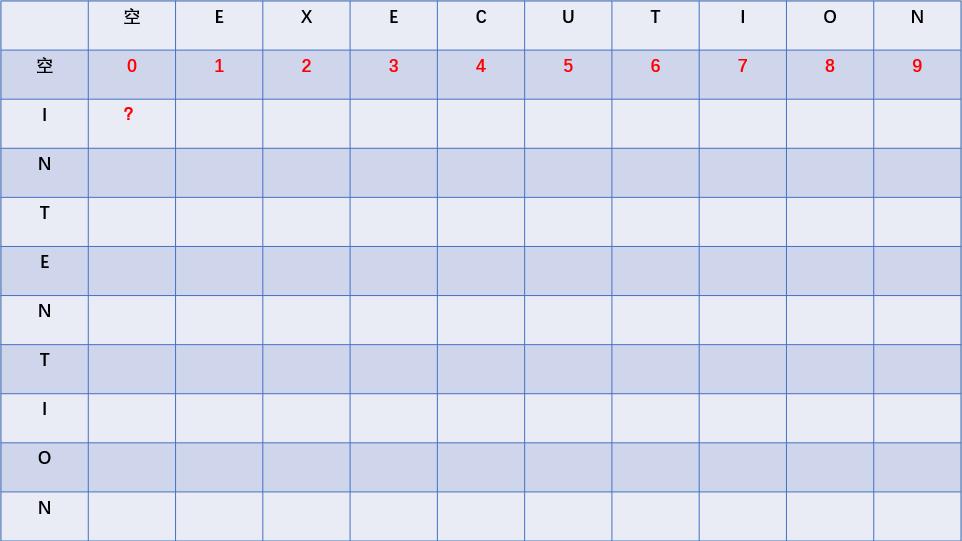
上图我们又标了一个有问号的单元格，这里表示的是“空”字符串和“I”之间的距离，这个距离显然是1，所以，我们可以把1填进去。与上面几步类似，我们自上而下可以分别填写“空”字符串与“IN”、“INT”、“INTE”等字符串之间的距离，如下图：

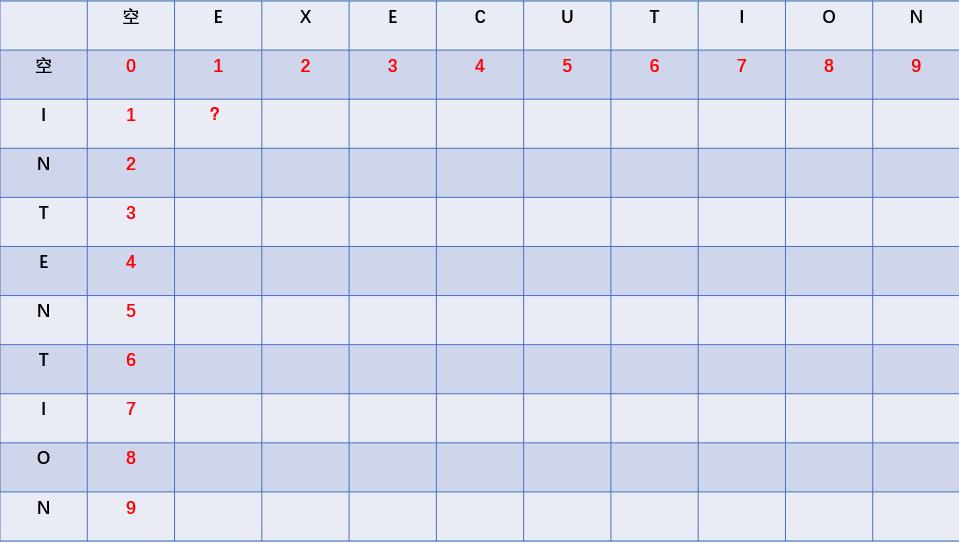
接下来就是特别重要的一个单元格了，也就是上图中问号标记的那个单元格。这个单元格表示的是字符串“E”和字符串“I”之间的的编辑距离，因为这两个字符串不一样，所以需要进行1步“替换”操作，因此我们在这里填上1。

（主要特别特别注意的是：关于“替换”操作是1步还是2步的问题，大家一定要看清楚前提条件，因为有些场景下，“替换”等于先删除再添加，即2步，而有些场景下，“替换”是1步。我们这里认为“替换”是1步。）

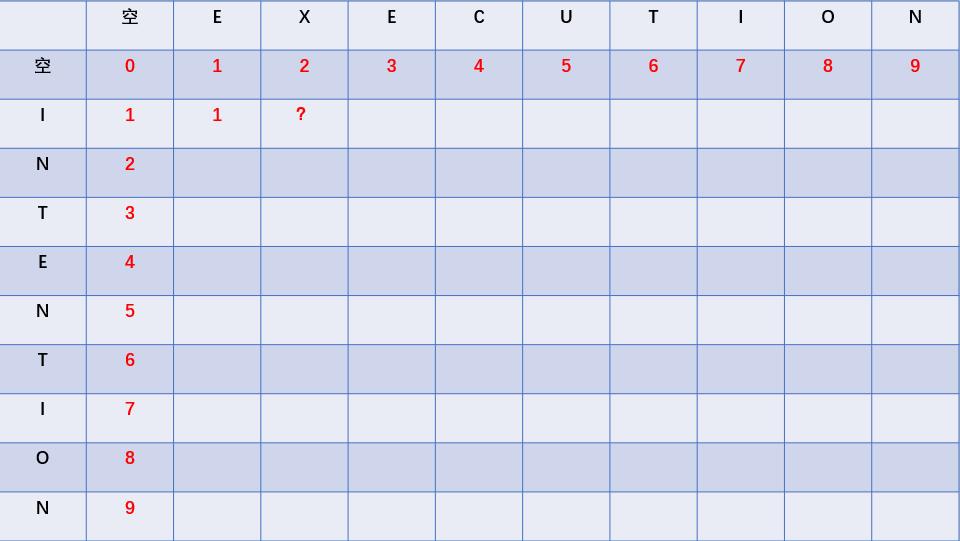
这时候我们又看到了一个新的问号，它代表的是字符串“EX”和字符串“I”之间的距离，这个时候我们就要分三种情况了：

第一种：

“E”和“I”之间的距离+1，即：1+1=2

第二种：

“EX”和“空”字符串之间的距离+1，即：2+1=3

第三种：

“E”和“空”字符串之间的距离+1，即：1+1=2

这三个距离中最短的距离是2，所以“EX”和“I”之间的最短编辑距离是2，如下图：

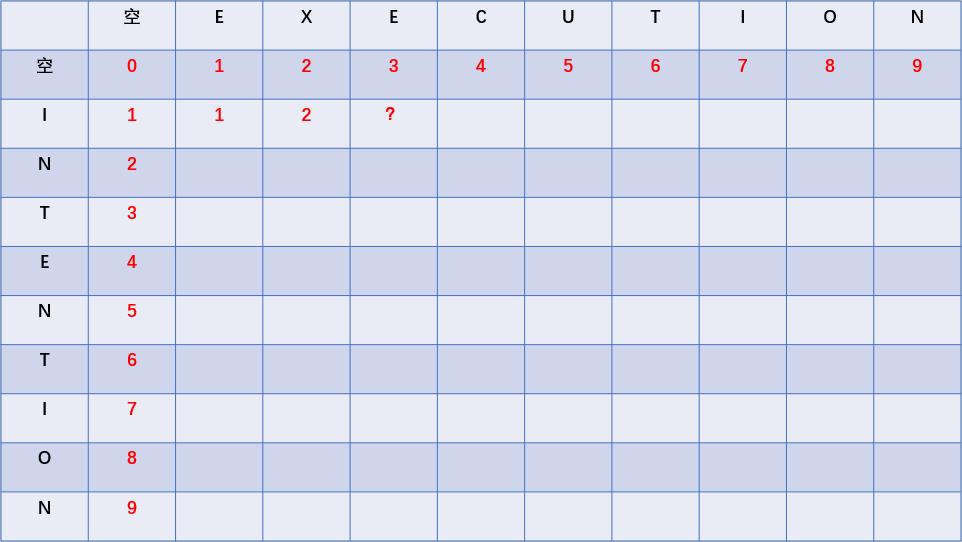
大家仔细观察上图，会发现下面这种情况：

也就说实际上我们计算的是一个单元格的左侧、上侧和左斜上侧的三个单元格的值分别加1后所得到的三个值中最小的那个值。

为了验证真假，我们来算一下前一个图中标问号的单元格的值，如果按照上述方法应该是：

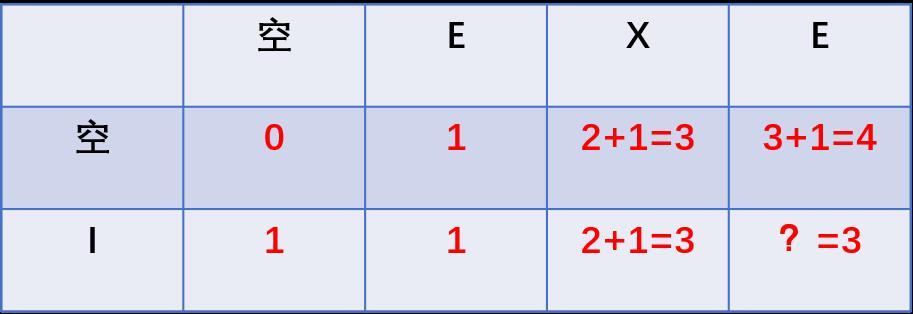
即：“EXE”和“I”的最短编辑距离为3。我们直接计算都能看出来，这个结果显然是正确的。第一步删除一个E、第二步删除一个X、第三步将E替换为I，这样用3步就完成了从“EXE”到“I”的转换。

我们再用三种情况分别分析一下：

第一种：

“EX”和“I”之间的距离+1，即：2+1=3

第二种：

“EXE”和“空”字符串之间的距离+1，即：3+1=4

第三种：

“EX”和“空”字符串之间的距离+1，即：2+1=3

以上三个值中最小的是3，所以“EXE”和“I”的最短编辑距离为3。

这样我们就再次验证了这种计算方法的可行性。

于是乎，我们就可以“大开算戒”，逐个计算每一个单元格中的值，直到算到最右下角的单元格的值。但一定要注意，还有特殊情况，如下图：

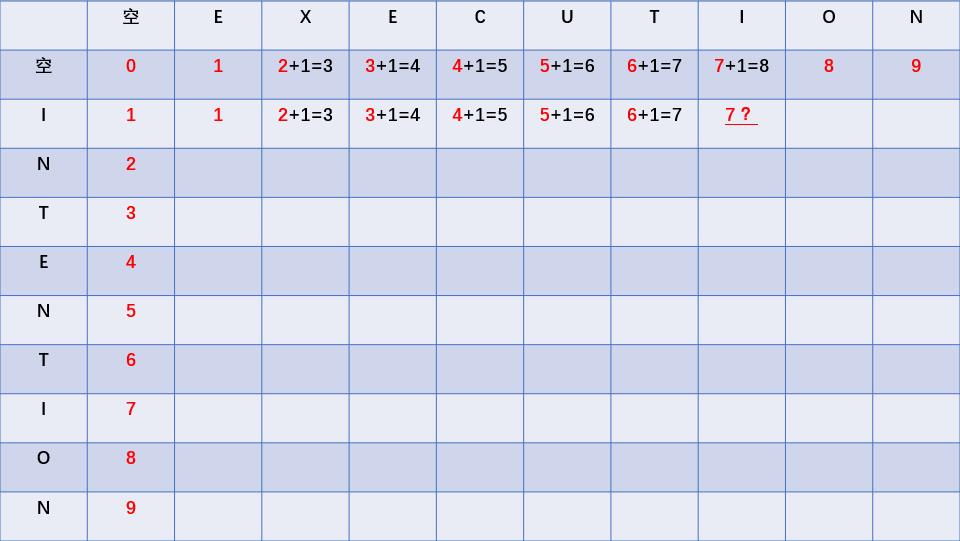
当我们愉快地计算，并算到上图标问号的单元格时，如果还是按照上面的方法我们就会得到一个7。但这个7是错误的！

我们来看一下这个单元格代表的是什么：

字符串“EXECUTI”和字符串“I”之间的距离。

这时候，两个字符串的最后一位是一样的！

所以，相当于我们在计算“EXECUT”和“空”字符串之间的距离，显然这个距离是6！

所以，我们应该在上面填写6，而不是7。

像上面这种情况这个表格中还有几处：

所以每当计算某个单元格的值时，要先判断一下要比较的两个字符串的最后一位是否一样，如果一样，那么它的取值就应该等于左斜上角单元格的取值，而非左、上和左斜上三个单元格取值各加一后的最小值。

如此一来，我们再往下计算就不会遇到什么障碍了，我把整个表格完成的结果贴到下面：

上面这个图中，红色的数字都是单元格内本应该填写的数字，后面的加法过程和结果用黑色来表示，这些是用来做推导的。橘黄色箭头表示我们在对应的单元格内计算的两个字符串的最后一位是一样的，所以我们沿用左斜上侧的结果。

结语

通过上面这一通描述，我希望我已经用最浅显易懂的语言来解释如何用“动态规划”的算法来计算两个字符串之间的最短编辑距离了，如果大家还有不明白的，可以在下方留言，我们一起来探讨。

在下一篇文章中，我准备分享如何通过编程让计算机自动来计算，而不是用上面这个表格来一步步推算。