动态规划_最长上升子序列plus_最短编辑距离

Posted 2021-09-17 一只特立独行的猫

目录

• • 最长上升自序列plus
  • • 题目大意
    • 思路：
    • 代码：
  • 最短编辑距离
  • • 题目大意：
    • 思路：
    • 代码：

最长上升自序列plus

题目大意

给定一个长度为 N 的数列，求数值严格单调递增的子序列的长度最长是多少。
0<N<100000;
原题链接
（相较于一般的O(n^2)复杂度的dp算法，由于扩大了数据量到1e5，所以要通过改进的办法来解决。）

思路：

设置一个$p$数组，$p[i]$表示长度为i的数组的结尾的数字。设置这个数组的原因是我们可以发现如下规律。
对于任意一个递增子序列，如果在这个子序列后还存在一个比$p[i]$小，但是比$p[i-1]$大的数，那么这个数就可以取代$p[i]$,而这样取代以后，会减少下一个递增子序列的约束。利用贪心的思想，加上二分的手段，可以将时间复杂度降低到O(nlogn)。
用到了向右扩展取最小的一个大于等于x的一个数，坐标为r+1。

代码：

#include<iostream>

using namespace std;

const int N = 1e5+5;

int a[N],p[N];

int main(){
    int n;
    cin>>n;
    for(int i=0;i<n;i++) scanf("%d",&a[i]);
    
    int len=0;
    p[0]=-1e9-5;
    for(int i=0;i<n;i++){
        //二分
        int l=0,r=len;
        while(l<r){
            int mid=(l+r+1)>>1;
            if(p[mid]<a[i]) l=mid;
            else r=mid-1;
        }
        cout<<r<<" "<<l<<endl;
        len=max(len,r+1);
        p[r+1]=a[i];
    }
    cout<<len<<endl;
    return 0;
}

最短编辑距离

题目大意：

给定两个字符串 A 和 B，现在要将 A 经过若干操作变为 B，可进行的操作有：
删除–将字符串 A中的某个字符删除。
插入–在字符串 A的某个位置插入某个字符。
替换–将字符串 A中的某个字符替换为另一个字符。

现在请你求出，将 A变为 B 至少需要进行多少次操作。
原题链接

思路：

$f(i,j)$表示a字符的前i个字符和b字符串的前j个字符相等需要执行的操作步骤。

所以，$f(i,j)$的状态可以由以下三种种状态转移而来。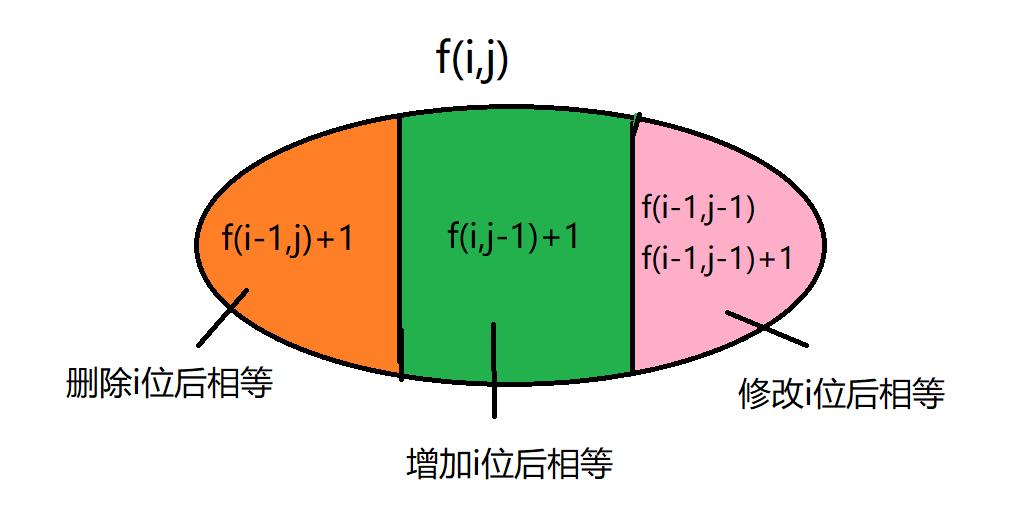

代码：

#include<iostream>

using namespace std;

const int N = 1e3+5;

int n,m,f[N][N];
char a[N],b[N];

int main(){
    scanf("%d%s",&n,a+1);
    scanf("%d%s",&m,b+1);
    
    for(int i=0;i<=n;i++) f[i][0]=i;//删完
    for(int i=0;i<=m;i++) f[0][i]=i;//增加i位
    
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            f[i][j]=min(f[i-1][j]+1,f[i][j-1]+1);
            if(a[i]==b[j]) f[i][j]=min(f[i][j],f[i-1][j-1]);
            else f[i][j]=min(f[i][j],f[i-1][j-1]+1);
        }
    }
    printf("%d",f[n][m]);
    return 0;
}