动态规划线性dp问题总结：数字三角形最长上升子序列最长公共子序列最短编辑距离 题解与模板

Posted 2022-03-23 karshey

是AcWing算法基础课动态规划线性dp的笔记。

AcWing 898. 数字三角形

题

#include<bits/stdc++.h>
using namespace std;
#define fir(i,a,n) for(int i=a;i<=n;i++)
#define mem(a,x) memset(a,x,sizeof(a));
#define INF 0x3f3f3f3f
typedef long long ll;
const int N=500+10;
int n;
int a[N][N],dp[N][N];
int main()

	cin>>n;
	fir(i,1,n)
		fir(j,1,i)
			cin>>a[i][j];
	fir(i,1,n)
		fir(j,1,i)
			dp[i][j]=-INF;
			
	dp[1][1]=a[1][1];
	fir(i,2,n)
		fir(j,1,i)
		
			if(j==1) dp[i][j]=dp[i-1][j]+a[i][j];
			else if(j==i) dp[i][j]=dp[i-1][j-1]+a[i][j];
			else dp[i][j]=max(dp[i-1][j],dp[i-1][j-1])+a[i][j];
		
	
	int maxn=-INF;
	fir(i,1,n)  maxn=max(maxn,dp[n][i]);

	cout<<maxn;
	return 0;

AcWing 895. 最长上升子序列

AcWing 895. 最长上升子序列
VictorWu 大佬的题解

O(n²)的方法：

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define INF 0x3f3f3f3f
#define fir(i,a,n) for(int i=a;i<=n;i++)
const int N=1e3+10;
int n;
ll a[N],dp[N];//dp[i]表示以a[i]结尾的数的最长上升子序列长度 
int main()

	cin>>n;
	fir(i,1,n) cin>>a[i];
	fir(i,1,n) dp[i]=1;//初始化全为1:最差也可以只有自己 
	
	fir(i,1,n)
		fir(j,1,i-1)		
			if(a[i]>a[j]) dp[i]=max(dp[i],dp[j]+1);
	
	ll maxn=0;
	fir(i,1,n) maxn=max(maxn,dp[i]);
	cout<<maxn;	
	return 0;

O(nlogn)的方法：

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define INF 0x3f3f3f3f
#define fir(i,a,n) for(int i=a;i<=n;i++)
const int N=1e3+10;
int n,a[N],dp[N];//dp[i]表示长度为i的最长上升子序列的末尾最小值 
int main()

	cin>>n;
	fir(i,1,n) cin>>a[i];
	
	int cnt=0;
	dp[cnt++]=a[1];//第一个初始化的数可以大但不能小 
	fir(i,1,n)
	
		if(a[i]>dp[cnt-1]) dp[cnt++]=a[i];
		else
		
			//更新当前的最长上升子序列的某个值使之保持一直最小
			int l=0,r=cnt-1;
			while(l<r)
			
				int mid=(l+r)/2;
				if(dp[mid]>=a[i]) r=mid;//我们要找的是大于w[i]的第一个dp 所以这里符合条件 r取到mid 
				else l=mid+1;
			
			dp[r]=a[i];
		
	
	cout<<cnt;
	return 0;

AcWing 896. 最长上升子序列 II

AcWing 896. 最长上升子序列 II
O(nlogn):
代码1：（其实就是上一个代码）

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define INF 0x3f3f3f3f
#define fir(i,a,n) for(int i=a;i<=n;i++)
const int N=1e3+10;
int n,a[N],dp[N];//dp[i]表示长度为i的最长上升子序列的末尾最小值 
int main()

	cin>>n;
	fir(i,1,n) cin>>a[i];
	
	int cnt=0;
	dp[cnt++]=a[1];//第一个初始化的数可以大但不能小 
	fir(i,1,n)
	
		if(a[i]>dp[cnt-1]) dp[cnt++]=a[i];
		else
		
			//更新当前的最长上升子序列的某个值使之保持一直最小
			int l=0,r=cnt-1;
			while(l<r)
			
				int mid=(l+r)/2;
				if(dp[mid]>=a[i]) r=mid;//我们要找的是大于w[i]的第一个dp 所以这里符合条件 r取到mid 
				else l=mid+1;
			
			dp[l]=a[i];
		
	
	cout<<cnt;
	return 0;

代码2：用栈来模拟上述过程，天秀。
参考：233 大佬的代码

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define INF 0x3f3f3f3f
#define fir(i,a,n) for(int i=a;i<=n;i++)
#define pb push_back
const int N=1e5+10;
int n,a[N];
vector<int>v;
int main()

	cin>>n;
	fir(i,1,n) cin>>a[i];
	v.pb(a[1]);
	fir(i,1,n)
	
		if(a[i]>v.back()) v.pb(a[i]);
		else 
		
			//找到第一个大于等于a[i]的，把它换掉
			//这样长度不变 但是最长上升子序列的序列最优 
			auto it=lower_bound(v.begin(),v.end(),a[i]);
			*it=a[i];
		
	
	cout<<v.size();
	return 0;

AcWing 897. 最长公共子序列

AcWing 897. 最长公共子序列
yuechen 大佬的题解

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define INF 0x3f3f3f3f
#define fir(i,a,n) for(int i=a;i<=n;i++)
const int N=1e3+10;
int n,m,dp[N][N];//dp[i][j]代表从a的1-i到b的1-j的最长公共子序列 
string a,b;
int main()

	cin>>n>>m>>a>>b;
	fir(i,1,n)
		fir(j,1,m)
		
			if(a[i-1]==b[j-1]) dp[i][j]=max(dp[i][j],dp[i-1][j-1]+1);
			else dp[i][j]=max(dp[i-1][j],dp[i][j-1]);
		
	cout<<dp[n][m];
	return 0;

AcWing 902. 最短编辑距离

AcWing 902. 最短编辑距离
Shadow 大佬的题解

题解中对状态转移和细节初始化的解释：

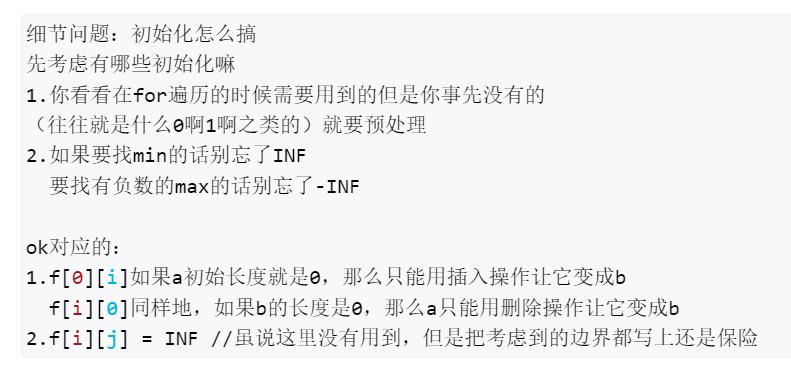
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define INF 0x3f3f3f3f
#define fir(i,a,n) for(int i=a;i<=n;i++)
const int N=1e3+10;
int n,m;string a,b;
int dp[N][N];
int main()

	cin>>n>>a>>m>>b;
	
	//初始化 
	memset(dp,0x3f,sizeof(dp));
	dp[0][0]=0;//都是空串的时候自然相等 且不用操作 
	fir(i,1,n) dp[i][0]=i;
	fir(i,1,m) dp[0][i]=i;
	
	//dp
	fir(i,1,n)
		fir(j,1,m)
		
			//string从0开始
			if(a[i-1]==b[j-1]) dp[i][j]=dp[i-1][j-1];
			else dp[i][j]=min(dp[i-1][j],dp[i][j-1],dp[i-1][j-1])+1;
		
	cout<<dp[n][m];
	return 0;

AcWing 899. 编辑距离

AcWing 899. 编辑距离
是对上一个模板题的应用。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define INF 0x3f3f3f3f
#define fir(i,a,n) for(int i=a;i<=n;i++)
const int N=1e3+10;
int n,m,t;
string a[N],b;
int dp[15][15];//a b
int GetDis(int u)

	string c=a[u];
	memset(dp,0x3f,sizeof(dp));
	dp[0][0]=0;
	fir(i,1,c.size()) dp[i][0]=i;
	fir(j,1,b.size()) dp[0][j]=j;
	
	fir(i,1,c.size())
		fir(j,1,b.size())
		
			if(c[i-1]==b[j-1]) dp[i][j]=dp[i-1][j-1];
			else dp[i][j]=min(dp[i-1][j],dp[i][j-1],dp[i-1][j-1])+1;
		
	if(dp[c.size()][b.size()]<=t) return 1;
	else return 0;

int main()

	cin>>n>>m;
	fir(i,1,n) cin>>a[i];
	while(m--)
	
		cin>>b>>t;
		int ans=0;
		fir(i,1,n)
			if(GetDis(i)) ans++;
		cout<<ans<<endl;
	
	return 0;