前端算法之动态规划

Posted 2021-04-18 开课吧前端团队

来源：编程鹿子

https://www.toutiao.com/i6857090259818119683/

动态规划整体思路是用递归问题求解，然后对递归过程中存在的大量重叠子问题进行优化；

自顶向下的求解的思路为记忆化搜索，自底向上的解决问题的思想就是动态规划，自顶向下的求解通常更好理解，我们理解后在改成自底向上的动态规划求解；

剑指 Offer 10- I. 斐波那契数列

写一个函数，输入 n ，求斐波那契（Fibonacci）数列的第 n 项。斐波那契数列的定义如下：

F(0) = 0, F(1) = 1

F(N) = F(N - 1) + F(N - 2), 其中 N > 1.

斐波那契数列由 0 和 1 开始，之后的斐波那契数就是由之前的两数相加而得出。

答案需要取模 1e9+7（1000000007），如计算初始结果为：1000000008，请返回 1。

示例 1：输入：n = 2输出：1示例 2：输入：n = 5输出：5

斐波那契的思想，就是我们求fib(n) 的解转化为我们求 fib(n-1)+fib(n-2) ,fib(n-1) 我们可以转化为 fib(n-1-1) + fib(n-2-1) ，随着递归进行，我们最后会得到n=1和 n=0的时候，同时我们知道 n=0时fib(0) 等于0 fib(1)等于1，

/** * @param {number} n * @return {number} */var fib = function(n) { if(n==0){ return 0  } if(n==1){ return 1 } return fib(n-1) +fib(n-2)};

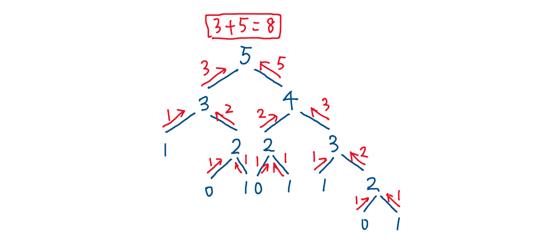
上述代码实现了一个斐波那契数列，但是对于斐波那契数列数列的时间复杂度是o的n次方的；

因为我们求解的时候存在大量的重复求解，在上面的基础上运用cache 缓存计算结果 cache[n] 存在时直接求解，防止重复计算

/** * @param {number} n * @return {number} */var fib = function(n) {  const cache = { 0:0n, 1:1n, }; return Fibonacci(n) % 1000000007n; function Fibonacci(n){ if(cache[n]!==undefined) { return cache[n] } cache[n] = Fibonacci(n - 1) + Fibonacci(n - 2) return cache[n]; } };

我们改造成动态规划的求解方式，自下向上的解决问题，

fibonacci = 0 时 fib(0) 为0 fibonacci 为1时fib(1) =1 fibonacci[2] = fibonacci[2-1] + fibonacci[2-2] ，

我们求n的解只需求解 fibonacci[n]

/** * @param {number} n * @return {number} */var fib = function(n) { let fibonacci = [0,1]; for(let i = 2; i <= n; i ++) { fibonacci[i] = (fibonacci[i - 1] + fibonacci[i - 2]) % (1e9 +7); } return fibonacci[n];};

我们再看一个典型的斐波那契问题

爬楼梯

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。

每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

注意：给定 n 是一个正整数。

示例 1：

输入：2输出：2解释：有两种方法可以爬到楼顶。1. 1 阶 + 1 阶2. 2 阶

解题：该题和上题思路相同，我们就不深入讲解了，我们使用记忆结果时可以使用对象，也可以使用数组

自顶向下求解

/** * @param {number} n * @return {number} */var climbStairs = function (n,map={1:1,2:2}) { if (map[n]) return map[n]; else map[n]=map[n-1]+map[n-2]; return climbStairs(n - 1,map) + climbStairs(n - 2,map);};

自底向上求解

/** * @param {number} n * @return {number} */var climbStairs = function (n) { let catche = [1,1] for(let i=2;i<=n;i++){ catche[i] = catche[i-1] +catche[i-2]  } return catche[n]};

整数拆分

给定一个正整数 n，将其拆分为至少两个正整数的和，并使这些整数的乘积最大化。

返回你可以获得的最大乘积。

示例 1:输入: 2输出: 1解释: 2 = 1 + 1, 1 × 1 = 1。示例 2:输入: 10输出: 36解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36。

解题：

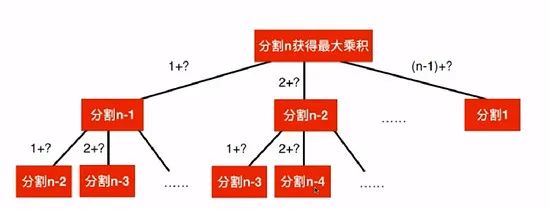
我们求分割n获得的最大乘积，需要求把n分成 1和n-1的成绩 2和n-2 的成绩 到n-1和1的最大成绩，在这个结果中取最大值

每次n可以选择当前值，或者i*(n-i) 不在分割n，和i* 继续分割n-i的结果i*d(n-i)

我们定义dp对象缓存n的最大值的结果，防止重复求解

/** * @param {number} n * @return {number} */var integerBreak = function(n) { // 定义dp缓存已求解的n的最大值 const dp = {} function d(n){ if(n==1){ return 1 } if(dp[n]!==undefined){ return dp[n] } let res = -1 for(let i =1;i<n;i++){ res = Math.max(res,i*(n-i),i*d(n-i)) } dp[n] = res return dp[n] } return d(n)};

解题二

状态数组dp[i]表示：数字 i 拆分为至少两个正整数之和的最大乘积。为了方便计算，dp 的长度是 n + 1，值初始化为 1。

显然dp[2]等于 1，外层循环从 3 开始遍历，一直到 n 停止。内层循环 j 从 1 开始遍历，一直到 i 之前停止，它代表着数字 i 可以拆分成 j + (i - j)。

但 j * (i - j)不一定是最大乘积，因为i-j不一定大于dp[i - j]（数字i-j拆分成整数之和的最大乘积），这里要选择最大的值作为 dp[i] 的结果。

空间复杂度是 O(N)O(N)，时间复杂度是 O(N^2)O(N的2次方）

/** * @param {number} n * @return {number} */var integerBreak = function(n) { const dp = new Array(n + 1).fill(1); for (let i = 3; i <= n; ++i) { for (let j = 1; j < i; ++j) { // 每次尝试将n分割为 j+(i-j)的值 dp[i] = Math.max(dp[i], j * (i - j), j * dp[i - j]); } } return dp[n];};

打家劫舍

你是一个专业的小偷，计划偷窃沿街的房屋。

每间房内都藏有一定的现金，影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警。

给定一个代表每个房屋存放金额的非负整数数组，计算你 不触动警报装置的情况下 ，一夜之内能够偷窃到的最高金额。

示例 1：

输入：[1,2,3,1]输出：4解释：偷窃 1 号房屋 (金额 = 1) ，然后偷窃 3 号房屋 (金额 = 3)。偷窃到的最高金额 = 1 + 3 = 4 。

解题：

对于一个房间我们可以选择偷取也可以选择不偷取，如果偷取的话我们下次选择需要选择n+2的房间来尝试偷取，结果取最大值

我们求解的值是不考虑偷取当前房间和考虑偷取当前房间的最大值 ，res = Math.max(res,nums[i]+room(nums,i+2)) ， 因为i+2 可能越界，因此当nums.length<=index时我们直接return 0

我们用tests 储存是否已经偷过该房间，如果tests访问过直接返回值，如果没有访问过，我们把求解的n的值储存在tests中

/** * @param {number[]} nums * @return {number} */var rob = function(nums) { let tests = new Array(nums.length).fill(-1) function room(nums,index){ if(nums.length<=index){ return 0 } if(tests[index]!==-1){ return tests[index] } let res = 0 for(let i =index;i<nums.length;i++){ res = Math.max(res,nums[i]+room(nums,i+2)) } tests[index] = res return tests[index] } return room(nums,0) };

解法2

动态规划方程：dp[n] = MAX( dp[n-1], dp[n-2] + num )

由于不可以在相邻的房屋闯入，所以在当前位置 n 房屋可盗窃的最大值，要么就是 n-1 房屋可盗窃的最大值，要么就是 n-2 房屋可盗窃的最大值加上当前房屋的值，二者之间取最大值。

举例来说：1 号房间可盗窃最大值为 33 即为 dp[1]=3，2 号房间可盗窃最大值为 44 即为 dp[2]=4，3 号房间自身的值为 22 即为 num=2，那么 dp[3] = MAX( dp[2], dp[1] + num ) = MAX(4, 3+2) = 5，3 号房间可盗窃最大值为 55

时间复杂度：O(n)O(n)，nn 为数组长度

/** * @param {number[]} nums * @return {number} */var rob = function(nums) { const len = nums.length; if(len == 0) return 0; const dp = new Array(len + 1); dp[0] = 0; dp[1] = nums[0]; for(let i = 2; i <= len; i++) { dp[i] = Math.max(dp[i-1], dp[i-2] + nums[i-1]); } return dp[len];};

你“在看”我吗？