迪杰斯特拉算法(Dijkstra) (基础dij+堆优化) BY:优少
Posted tonyshen
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了迪杰斯特拉算法(Dijkstra) (基础dij+堆优化) BY:优少相关的知识,希望对你有一定的参考价值。
首先来一段百度百科压压惊。。。
迪杰斯特拉算法(Dijkstra)是由荷兰计算机科学家狄克斯特拉于1959 年提出的,因此又叫狄克斯特拉算法。是从一个顶点到其余各顶点的最短路径算法,解决的是有权图中最短路径问题。迪杰斯特拉算法主要特点是以起始点为中心向外层层扩展,直到扩展到终点为止。
让我来翻译一下:
Dijkstra可以求出一个点到一个图中其他所有节点的最短路径,故也称对于单源最短路径的一种解法
算法实现步骤:
a.初始时,只包括源点,即S = {v},v的距离为0。U包含除v以外的其他顶点,即:U ={其余顶点},若v与U中顶点u有边,则(u,v)为正常权值,若u不是v的出边邻接点,则(u,v)权值 ∞;
b.从U中选取一个距离v最小的顶点k,把k,加入S中(该选定的距离就是v到k的最短路径长度)。
c.以k为新考虑的中间点,修改U中各顶点的距离;若从源点v到顶点u的距离(经过顶点k)比原来距离(不经过顶点k)短,则修改顶点u的距离值,修改后的距离值的顶点k的距离加上边上的权。
d.重复步骤b和c直到所有顶点都包含在S中。
动画模拟:
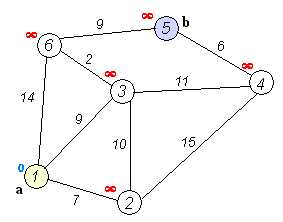
普通版Dijkstra代码如下:
#include<iostream> #include<cstdio> #include<cstdlib> #include<cstring> using namespace std; int map[100][100]; int vis[100]; int way[100]; int n,e,w,s; int main(){ freopen("dij.in","r",stdin); freopen("dij.out","w",stdout); int i,j,x,y,z,w,mi=20000; scanf("%d%d",&n,&e); for(i=1;i<=e;i++) { scanf("%d%d%d",&x,&y,&z); map[x][y]=z; map[y][x]=z; } memset(way,127,sizeof(way)); scanf("%d",&s); way[s]=0; for(i=1;i<n;i++) { for(j=1;j<=n;j++) if(way[j]<mi&&vis[j]==0) { mi=way[j]; w=j; } vis[w]=1; for(j=1;j<=n;j++) if(map[w][j]!=0&&vis[j]==0&&way[j]>way[w]+map[w][j]) way[j]=way[w]+map[w][j]; } for(i=1;i<=n;i++) printf("%d ",way[i]); return 0; }
那现在让我们分析一下复杂度,很明显高达O(N*N),那当做一些题时不论内存还是时间都会爆,那就急需我们做一些优化了
Dijkstra的堆优化:
依旧是迪杰斯特拉算法的思想,寻找当前距离最小的点,然后将它标记为已经确定的点,用它来更新各个没被确定的点。
emmmm我们选择优先队列来确定每一个最小距离的点
例题:
代码如下:
#include<bits/stdc++.h> using namespace std; struct SYM{ int to,next,w; }edge[500010]; struct LKJ{ int v,c; bool operator <(const LKJ &a)const { return c>a.c; } }; priority_queue<LKJ,vector<LKJ> > q; int head[101000],vis[101000],tot,dis[101000],n,m,k; void add(int x,int y,int w){ edge[++tot].to=y; edge[tot].w=w; edge[tot].next=head[x]; head[x]=tot; } void dij(int s){ dis[s]=0; LKJ hh;hh.v=s;hh.c=0; q.push(hh); while(!q.empty()){ LKJ tmp=q.top();q.pop(); int x=tmp.v; if(vis[x]) continue;vis[x]=1; for(int i=head[x];i;i=edge[i].next) if(!vis[edge[i].to]&&dis[edge[i].to]>dis[x]+edge[i].w){ dis[edge[i].to]=dis[x]+edge[i].w; hh.v=edge[i].to;hh.c=dis[edge[i].to]; q.push(hh); } } } int main(){ memset(dis,127,sizeof(dis)); int x,y,w; scanf("%d%d%d",&n,&m,&k); for(int i=1;i<=m;i++){ scanf("%d%d%d",&x,&y,&w); add(x,y,w); } dij(k); for(int i=1;i<=n;i++){ if(dis[i]==2139062143) printf("2147483647 "); else printf("%d ",dis[i]); } return 0; }
以上是关于迪杰斯特拉算法(Dijkstra) (基础dij+堆优化) BY:优少的主要内容,如果未能解决你的问题,请参考以下文章
(王道408考研数据结构)第六章图-第四节4:最短路径之迪杰斯特拉算法(思想代码演示答题规范)