数据结构 图 最短路径问题 迪杰斯特拉算法和弗洛伊德算法问题

Posted 2023-04-30

求解下面两句话都错在什么地方？
（1）求从指定原点到其余各顶点的迪杰斯特拉最短路径算法中弧上权值不能为负的原因是在实际应用中无意义
（2）弗洛伊德求每对不同顶点对的算法中允许弧上的权值为负，但不能有权值和为负的回路

1. dijkstra 不能有负权边，否则结果是错的，你想想，假如无向图有1,2,3个点，w(1,2)=1,w(1,3)=2,w(2,3)=-2. 按dij算法求求看。
2.这句话还没找到反例...不过教floyd时说是用在非负权边上的，除了负的回路之外应该还有漏洞吧.. 参考技术A 同意下面的看法,你很枪

最短路径（迪杰斯特拉算法）

1 构造图

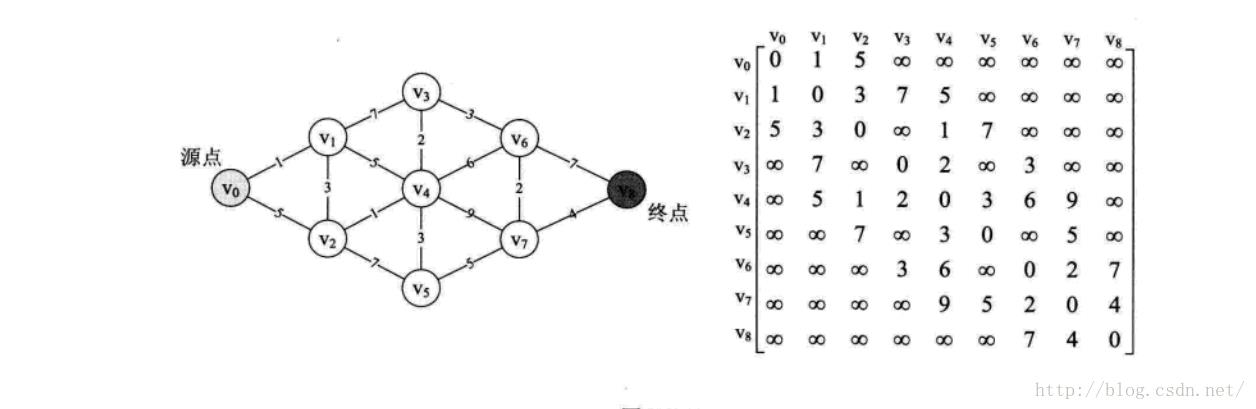
2 代码

package leaning.graph;

/*
 * 迪杰斯特拉算法求最短路径
 * 
 * */
public class Dijkstra 
	
	// 表示V0顶点到v8顶点的最短路径的值
	private int[] D = new int[9]; 
	
	// 最短路径
	private  int[] P = new int[9]; 
	
	//定义无穷大的数
	private int MAX = Integer.MAX_VALUE/2;
	
	//定义地图变量
	private int[][] map = new int[9][9];
	
	//定义顶点变量
	private String[] points = "v0","v1","v2","v3","v4","v5","v6","v7","v8";
	
	//初始化地图
	public void createMap()
		this.map[0] = new int[]  0,  1,  5,MAX,MAX,MAX,MAX,MAX,MAX;
		this.map[1] = new int[]  1,  0,  3,  7,  5,MAX,MAX,MAX,MAX;
		this.map[2] = new int[]  5,  3,  0,MAX,  1,  7,MAX,MAX,MAX;
		this.map[3] = new int[]MAX,  7,MAX,  0,  2,MAX,  3,MAX,MAX;
		this.map[4] = new int[]MAX,  5,  1,  2,  0,  3,  6,  9,MAX;
		this.map[5] = new int[]MAX,MAX,  7,MAX,  3,  0,MAX,  5,MAX;
		this.map[6] = new int[]MAX,MAX,MAX,  3,  6,MAX,  0,  2,  7;
		this.map[7] = new int[]MAX,MAX,MAX,MAX,  9,  5,  2,  0,  4;
		this.map[8] = new int[]MAX,MAX,MAX,MAX,MAX,MAX,  7,  4,  0;
	
	
	//迪杰斯特拉算法核心
	public void dijkstraCore()
	  // 1 定义变量
	  int[] final_ = new int[9] ; // final_[w]=1 表示已经从顶点V0访问了顶点Vw
	
	  // 2 初始化定义变量
	  for(int i = 0 ; i < this.points.length ;i++)
		  final_[i] = 0;
		  P[i] = 0;
		  D[i] = this.map[0][i];
	  
	  // 3 V0 -> V0节点
	      final_[0] = 1; 
	  // 4 V0 -> 其它节点
	     for(int i = 1 ; i < this.points.length ;i++)
	    	 int min = this.MAX ;
	    	 int k = -1;
	    	// 4.1 得到D带权数组最小值
	    	 for(int j = 0 ; j < this.points.length ; j++ )
	    		 if( final_[j]!=1 && min > D[j])
	    			 min = D[j];
	    			 k = j;
	    		 
	    	 
	    	 final_[k] = 1;
	    	// 4.2 调整 P和D的值
	    	 for(int j = 0 ; j < this.points.length ;j++)
	    		 if(final_[j]!=1 && ( min + this.map[k][j] ) < D[j] )
	    			D[j] = min + this.map[k][j];
	    			P[j] = k;
	    		 
	    	 
	    	 
	      
	    
	
	
	// 输出v0顶点到pointName顶点的最短路径
	public void show(String pointName)
		int position = getNumber(pointName);
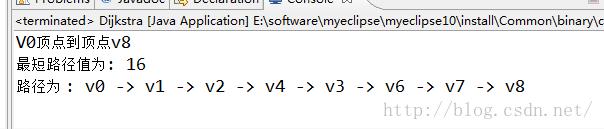
		System.out.println("V0顶点到顶点"+pointName+"\\n最短路径值为: "+this.D[position] + " \\n路径为 : " + this.getPath(pointName));
	
	
	// 得到v0顶点到pointName顶点的路径
	public String getPath(String pointName)
		StringBuffer path = new StringBuffer();
		path.append(this.invertStr(pointName));
		int position = getNumber(pointName);
		int point = this.P[position];
		while(point!=0)
			path.append(" >- " + this.invertStr(this.points[point]) );
			point = this.P[point];
		
		String pathString = path.append(" >- " + this.invertStr("v0") ).toString();
		return this.invertStr(pathString);
	
	
	// 得到字符串从后往前顺序的结果
	public String invertStr(String str)
		StringBuffer result = new StringBuffer();
		for(int i = str.length() -1 ; i >= 0 ; i-- )
			result.append(str.charAt(i));
		
		return result.toString();
	
	
	// 得到pointName在points数组中的位置
	public int getNumber(String pointName)
		int position = -1;
		for(int i = 0 ;  i < this.points.length ;i++  )
			if(this.points[i].endsWith(pointName.replace(" ", "")))
				position = i;
				break;
			
		
		return position;
	
	
	public static void main(String[] args) 
		Dijkstra dijkstra = new Dijkstra();
		dijkstra.createMap();
		dijkstra.dijkstraCore();
		dijkstra.show("v8");
	

3 变量D和变量P解释

4 v0到v8输出结果

开发者涨薪指南 48位大咖的思考法则、工作方式、逻辑体系