图论应用 floyd（弗洛伊德）算法dijkstra（迪杰斯特拉）算法

Posted 2021-08-30 踩踩踩从踩

前言

图论应用是非常广泛的，不同于二叉树，二叉树是应用在数据存储结构提高查询效率的，而图论则是用在辅助决策系统中，求得最优化解的等等，而本篇文章中介绍的floyd（弗洛伊德）算法、dijkstra（迪杰斯特拉）算法 是分别用于解决多元路径和最短路径问题的。应用比较广泛。辅助决策系统中使用

弗洛伊德算法

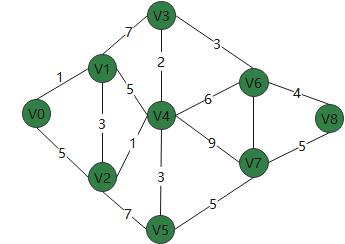
这个算法是为了解决多元路径问题的出现，从而找到最优的路径。 例如 下面的例子

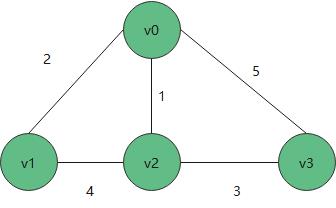
 从v1到v3之间的路径上有多种方式，但是权重是不相同的，两个节点之间得最短路径，用下图 邻接矩阵去表示

 弗洛伊德算法不管是有向图还是无向图，都能统计出一个节点到另一个节点最短路径，他可以找出整个图中节点之间得最短路径，所以叫多源最短路径算法。在算法实现中，通过邻接矩阵去实现。

算法分析

• 从v0开始，找每个节点得最短路径，把v0给锁住

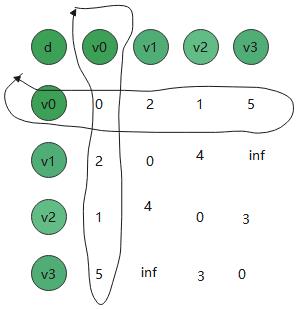
 第一行 就是 v0到v1 和 v0到v2 v0到v3 然后倒过来得距离， 这个初始值，有个点是在v0到v3，如果经过v2权重路径是比v0直接到v3路径短得。 也就是 5和4（3+1）得权重

所以 我们从v1开始 到v2 的最短路径，中转点了 我们从左开始不断进行看点修正

从v1走到v2路径

v1->v2 4

v1->v0->v2 2+1=3

明显经过中间点，就最近了

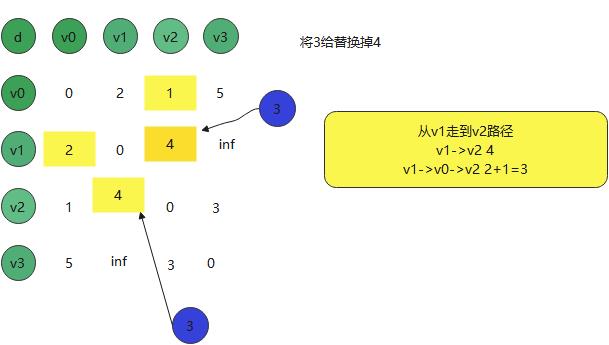
 已经就把以0为跳板将某个点进行修正了最短路径了。v1到v2 以0为中介转折点

 看v1到v3 从直观来看就是经过了两个节点，路径最小，因此有可能出现多个中转节点的情况

都经过算一次

 

 

 

 

这样得出最短路径 ，也就是不断修正数据，经过分析，从一个节点到另一个节点的最短路径

这样就能找到最短的路径了。

另外需要一个路径数据记录好修改的路径，这个需要记录上面的 更改的过程  路径更改的过程，当然这个路径可以任意取值的，我们注意的关键点在于值得修改

 

 

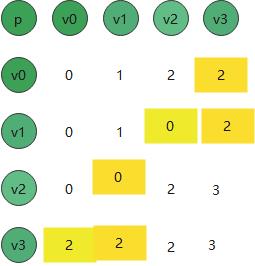
         这样我们就能记录好其中得跳板节点。

代码实现

首先我们先建两个邻接矩阵

  public static final int I = 100;
    //邻接距阵
    public static int[][] d = new int[][]{
            {0, 2, 1, 5},
            {2, 0, 4, I},
            {1, 4, 0, 3},
            {5, I, 3, 0}
    };
    public static int[][] p=new int[][]{
            {0,1,2,3},
            {0,1,2,3},
            {0,1,2,3},
            {0,1,2,3}
    };

而向矩阵中填数据，则预先填了，生成这个很简单就不用通过代码生成

然后弗洛伊德算法 方法

    public static void floyd(){
        for (int k = 0; k < d.length; k++) {
            for(int i=0;i<d.length;i++){
                for (int j = 0; j < d.length; j++) {
                    if(d[i][j]>d[i][k]+d[k][j]){
                        d[i][j]=d[i][k]+d[k][j];
                        //记录下路径
                        p[i][j]=p[i][k];
                    }
                }
            }
        }
    }

两层循环可以将二维数组都遍历得到， 遍历同时 d[i][j]>d[i][k]+d[k][j] 不断判断，也就是记录更小的数据，进行赋值，并将记录好变化的节点。

时间复杂度是n的三次方。经过三层循环就能找到对应的值，就是通过三层循环去找到对应的值。

迪杰斯特拉算法

上面的弗洛伊德算法算法去求任意两个顶点之间的最优路径问题，性能是比较低的，n的三次方法，但是不能改变的。 

而迪杰斯特拉算法，相当于弗洛伊德算法算法的提升，只需要求某个顶点到其他任意顶点的最短路径，起点只能从一个点开始

 

 

 

核心思想

我们用一个v0点为开始点，我们去查找到任意个点的最短路径。

• 首先建立两个集合，假设为U  和V   从那个节点开始，我们就先将节点放到U集合中

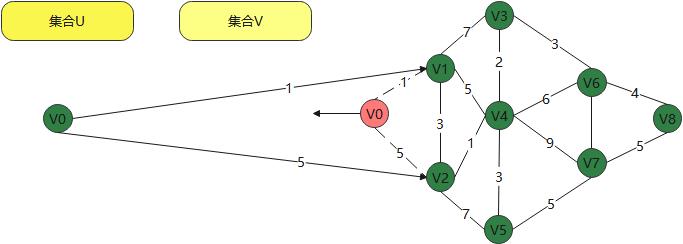
 以当前节点开始找到最短路径 如果小的路径，继续拿过来

 现在从v0到v2的路径有  经过v1和直到的两种方式，然后新建权重数组和路径数组，

权重数组保存经过的权重，而路径数组用来保存前面的顶点 

 这样不断的往前走，当到v3时，不可达，就直接跳过v3,到v4

 

 

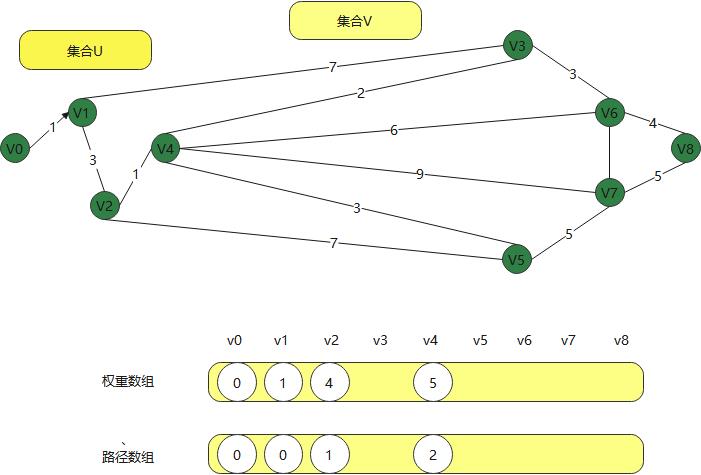
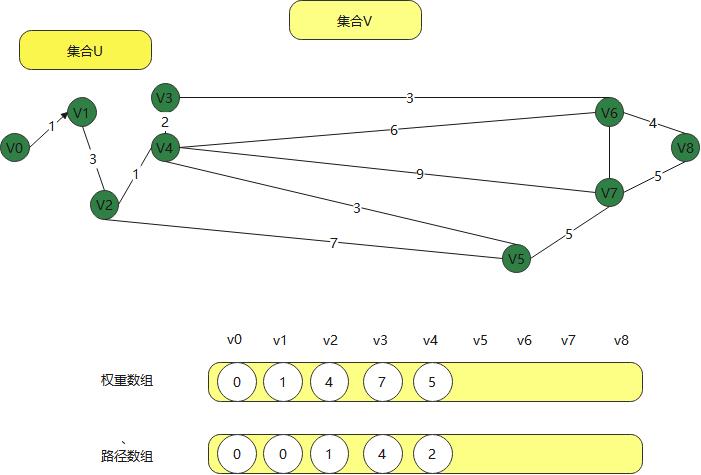
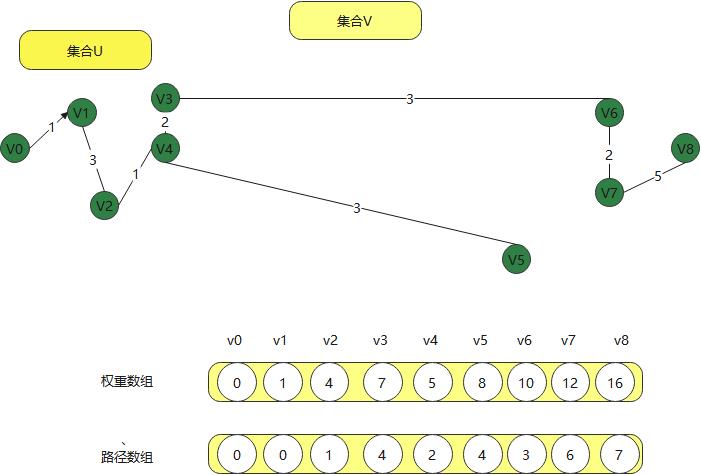
最后得到得到下面得权重和路径，

两个集合顶点，一直在计算和修正，这样就能找到一个顶点到后面顶点得最短路径，这就是迪杰斯特拉算法。

在代码中实现，是通过邻阶矩阵，左上进行看最大和最小。

代码实现

首先创建一个邻接矩阵

 public static final int I = 100;
    int[][] array=new int[][]{
            {0,1,5,I,I,I,I,I,I},
            {1,0,3,7,5,I,I,I,I},
            {5,3,0,I,1,7,I,I,I},
            {I,7,I,0,2,I,3,I,I},
            {I,5,1,2,0,3,6,I,I},
            {I,I,7,I,3,0,I,5,I},
            {I,I,I,3,6,I,0,2,7},
            {I,I,I,I,9,5,2,0,4},
            {I,I,I,I,I,I,7,4,0}
    };

处理顶点，首先要创建两个集合

 int k=0;//表示当前正要处理的顶点Vk
 //初始化相关的信息
 int[] path=new int[9];
 int[] weight=array[0];

 最开始表示v0智能到v1和v2,然后不断修正

 //定义一个数组来存放U和V两个集合的信息
        int[] flag=new int[9];

就开始逻辑进行修正数据了

 //开始逻辑,求VO到某个顶点的最短路径
        for(int v=1;v<9;v++){
            //在能走的路径中找到最短的一条
            int min=I;
            for(int i=0;i<9;i++){
                if(flag[i]==0 && weight[i]<min){
                    k=i;//K为U集合到V集合中找到的顶点
                    min=weight[i];//min找到了最小值的位置
                }
            }
            //从这个最短的路径对应的顶点开始找下一轮
            flag[k]=1;
            //修正当前最短路径
            for(int i=0;i<9;i++){
                //如果经过V顶点的路径比现在的路径短，新更新
                if(flag[i]==0 && (min+array[k][i])<weight[i]){
                    weight[i]=min+array[k][i];//修改路径长度
                    path[i]=k;//保存前驱
                }
            }
        }

按照之前得思路， 先选择 v0中最小权重得那个顶点，K为U集合到V集合中找到的顶点

 //在能走的路径中找到最短的一条
            int min=I;
            for(int i=0;i<9;i++){
                if(flag[i]==0 && weight[i]<min){
                    k=i;//K为U集合到V集合中找到的顶点
                    min=weight[i];//min找到了最小值的位置
                }
            }

从这个最短的路径对应的顶点开始找下一轮，这里得修正也是我们只会修正最上面行，weight 数组，以来保证最短的路径

 flag[k]=1;
            //修正当前最短路径
            for(int i=0;i<9;i++){
                //如果经过V顶点的路径比现在的路径短，新更新
                if(flag[i]==0 && (min+array[k][i])<weight[i]){
                    weight[i]=min+array[k][i];//修改路径长度
                    path[i]=k;//保存前驱
                }
            }

这里进行修正路径就是按照下面的方式进行修正，如果他下面的值加上左边的任意一个值，小于他就行修正，也就是min+array[k][i]<werght 则进行修改

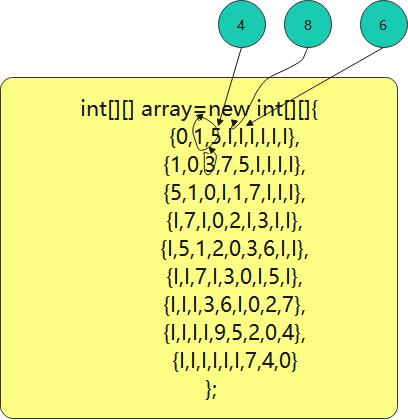
 也就是修正过后就为  [0,1,4,8,6,i,i,i,i],然后继续进行修正， 到2开始继续进行修正

就是继续标记下去，

flage[]={0,0,0,0....}

weight[]={0,1,5,i,i....}

path[]={0,0,0,0}

然后继续看下一行 {0,1,4,8,5,i,i,i,i}

int[][] array=new int[][]{
            {0,1,4,8,6,I,I,I,I},
           ,
            {5,1,0,I,1,7,I,I,I},
            {I,7,I,0,2,I,3,I,I},
            {I,5,1,2,0,3,6,I,I},
            {I,I,7,I,3,0,I,5,I},
            {I,I,I,3,6,I,0,2,7},
            {I,I,I,I,9,5,2,0,4},
            {I,I,I,I,I,I,7,4,0}
    };

 最后把值打印出来就行

   for(int i=0;i<path.length;i++){
            System.out.print(path[i]+" ");
        }
        System.out.println();
        for(int i=0;i<weight.length;i++){
            System.out.print(weight[i]+" ");
        }
//打印结果
        int v=8;
        while(v!=0){
            System.out.print(path[v]);
            v=path[v];
        }

在现实生活中如何去找到最短路径，我们可以提高效率这些

最小生成树

图论中的应用包括下面的最小生成树算法应用非常广泛，一个有 n 个结点的连通图的生成树是原图的极小连通子图，且包含原图中的所有 n 个结点，并且有保持图连通的最少的边。 [1]  最小生成树可以用kruskal（克鲁斯卡尔）算法或prim（普里姆）算法求出。

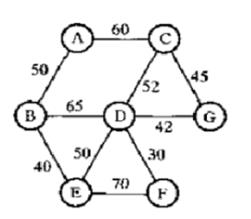
 克鲁斯卡尔(Kruskal) 算法

 

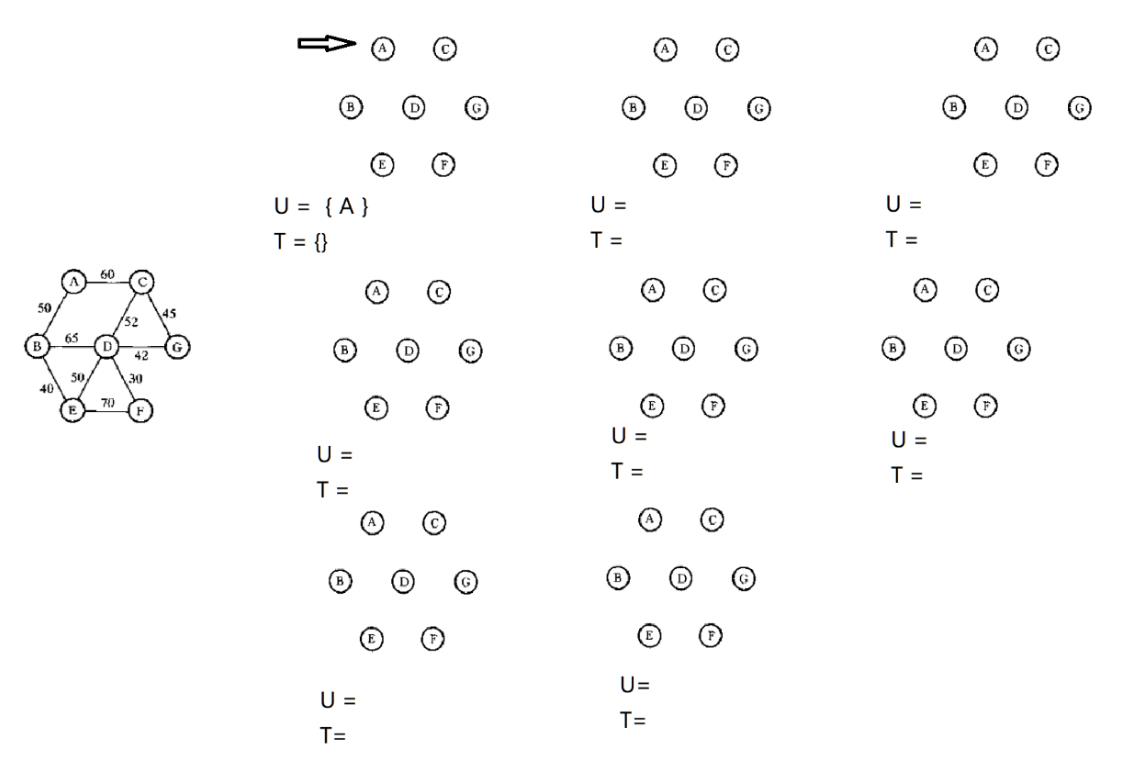
 这个算法也是图论算法中使用的，以边进行操作，点先进行排序，最小生成树

总结

图论的应用，弗洛伊德算法和迪杰斯特拉算法，的应用，都是为了寻找最短路径的。应用是相当广泛，提高程序性能，解决最短路径的问题，我们在学习这个算法，对提高自己技术是非常有用的。