一本通p1424 喷水装置

Posted 2021-03-17 huixinxinw

1424：【例题3】喷水装置

题目链接：http://ybt.ssoier.cn:8088/problem_show.php?pid=1424

时间限制: 1000 ms 内存限制: 65536 KB
提交数: 2578 通过数: 407
【题目描述】
长 L 米，宽 W 米的草坪里装有 n 个浇灌喷头。每个喷头都装在草坪中心线上（离两边各 W2 米）。我们知道每个喷头的位置（离草坪中心线左端的距离），以及它能覆盖到的浇灌范围。

请问：如果要同时浇灌整块草坪，最少需要打开多少个喷头？

【输入】
输入包含若干组测试数据。

第一行一个整数 T 表示数据组数；

每组数据的第一行是整数 n、L 和 W；

接下来的 n 行，每行包含两个整数，给出一个喷头的位置和浇灌半径（上面的示意图是样例输入第一组数据所描述的情况）。

【输出】
对每组测试数据输出一个数字，表示要浇灌整块草坪所需喷头数目的最小值。如果所有喷头都打开也不能浇灌整块草坪，则输出 ?1 。

分析

对于每一个喷头我们知道他的浇灌半径（如图中红线所示），又已知草坪宽度的一般（如图中绿线），那么我们可以利用勾股定理求出图中蓝线的长度。

喷头位置减去蓝线长度为喷头所能覆盖到的左端点，喷头位置减去蓝线为右端点。

要注意的一点是，如果圆形的半径小于等于w/2就无法浇灌到任何一段位置，在读入数据的时候要进行特判

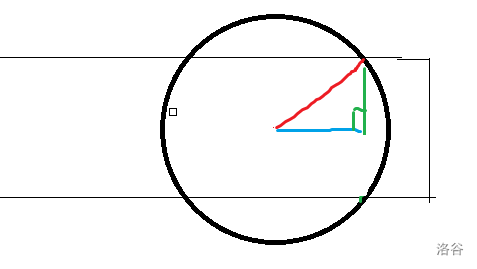
确定好每个喷头所覆盖的左右两个端点以后，我们按照左端点由小到大排序。

用一个指针记录最左边还未被覆盖的位置，在能覆盖到指针所在位置的喷头中，我们采取贪心的策略，选择其中右端点最远的一个喷头，并将指针所指的位置更新为其右端点的位置，直到整个草坪被完全覆盖。

如果指针记录的位置没有任何一个喷头能够那么就输出-1

（划重点）因为涉及到根号的运算，端点位置要用double类型来存储qwq

（因为没用double改了两个多小时。。。（肥宅暴风雨哭泣

Code

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath> 
#include<cstring>
#include<string> 
using namespace std;
int read(){
    int a = 0,f= 0;char p= getchar();
    while(!isdigit(p)){f|=p=='-';p = getchar();}
    while(isdigit(p)){a=(a<<3)+(a<<1)+(p^48);p = getchar();}
    return f?-a:a;
}//快读
struct qwq{
    double ll,rr;
}p[100000];//结构体来存储每个喷头浇灌的两个端点位置
bool cmp(qwq a,qwq b){
    return a.ll < b.ll;
}//按照左端点排序
bool flag[100000];
int main(){
    int t;
    t = read();
    while(t--){
        int cnt = 0; 
        memset(p,0,sizeof(p));//读入多组数据别忘了清空数组
        memset(flag,0,sizeof(flag));
        int n,L;
        double w;
        n = read();
        L = read();
        w = read();
        double wz,rr;
        for(int i = 1;i <= n;i ++){
            wz = read();
            rr = read();
            if(rr <= w/2)continue;//半径小于w/2的情况就跳过
            cnt ++;
            p[cnt].ll = wz - sqrt(rr*rr-(w/2)*(w/2));
            p[cnt].rr = wz + sqrt(rr*rr-(w/2)*(w/2));
        }
        sort(p + 1,p + cnt + 1,cmp);
        double l = 0,ans = 0;//用来记录当前所浇水浇到了哪里。
        int bj; 
        p[cnt+1].ll=2147483040；//要考虑最后一个喷头
        for(int i = 1;i <= cnt + 1 ;i++){
            if(l >= L)break;//都能浇灌上
            bj = 0;
            if(p[i].ll > l){//找到第一个覆盖不住当前左端点的点
                for(int j = i-1;j >= 1;j --){//这个点之前的点一定能覆盖到指针位置
                    if(!flag[j] && p[j].rr > l){//如果右端点大于指针位置
                        bj = j;
                        l = p[j].rr;
                    }
                }
                //cout<<bj<<" "<<l<<endl;
                if(bj == 0){cout << -1<<endl;break;}//指针位置没有喷头能覆盖到
                flag[bj] = 1;//更新指针
                ans++;//又多了一个喷头
            } 
        }
        if(bj != 0)cout << ans<<endl;//输出答案
    }
}