总结线段树

Posted 2021-03-15 huixinxinw

这篇博客是cyc的，看着挺容易懂的我就不再总结啦（滑稽

一个标准的板子，涉及到的只有一个叫做线段树的数据结构

First：线段树是什么？

线段树其实就是一棵二叉树，它将一个数列分成小区域，每个节点分别储存其对应的区间左右端点。

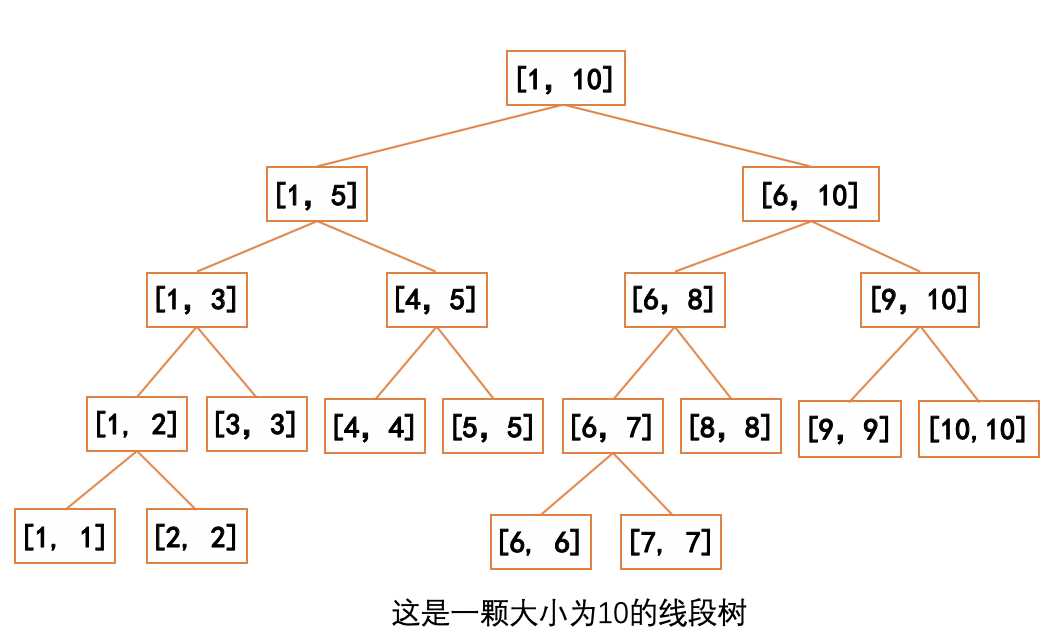
如图，设数组 a[n] ,图中 [ i,j ] 表示每一个二叉树结点对应的区间。容易发现，根节点对应的是整个区间 [ 0,n-1 ] 。一个结点对应的区间为 [ l,r ] ，当l=r时，它就是一个叶子结点，没有左右儿子；否则它就一定有左右两个儿子，存在mid=( l+r )/2，其左儿子为[ l,mid ]，右儿子对应区间为[ mid+1,r ]。

注意：这里左右儿子的分界一定要清晰、统一。如果这两个区间划分不清楚，就会（像我老师那样）翻车。

可以看出，二叉树高度h的复杂度只有O( logn )级别。

另外补充几点：

上面图中数组是[0,n-1]区间的，而下面我的代码区间为[1,n]。

二进制的位移运算 a * 2 = a << 1 ，表示a在二进制下向左移一位，也就是乘二。这种运算方式会比普通的 * 2 要快

Second：变量清单

//个人觉得写一个清单更有利于对于程序的规划，有计划总比没有强

变量： 线段树选择用结构体存储（t[ N ]），内含对应左右端点（l,r），对应区间的 区间和(sum)，以及后面会提到的懒标记两个(tag , tag_x)。

另外，代码中大量出现左右儿子，于是我写了一个求左右儿子编号的函数。

#define N 1000000+50//数据边界
struct tree{
    long long l,r,sum,tag,tag_x;//l,r左右端点，sum为结点对应区间和，tag为加法标记，tag_x为乘法标记 
}t[N];//线段树 
long long a[N];//输入的数列(1~n) 
long long m,n,p,k;//如题意(k是操作种类) 
long long ls(long long rt){return rt<<1;}//左孩子 
long long rs(long long rt){return rt<<1|1;}//右孩子 

Third：线段树操作

建树：

我们可以通过递归得到一棵二叉树，声明函数build（rt,l,r）,rt是线段树的结点，l,r 是这个结点对应的左右边界。如果 l=r，就是到达了叶节点，对应区间和t[rt] . sum等于a[i]。如果没有到达叶子结点，就可以通过build(ls(rt),l,mid)和build(rs(rt),mid+1,r)递归分别建立左右结点。最后更新rt的sum(维护区间和)，等于其左孩子的sum和右孩子的sum相加之和。

void build(long long rt,long long l,long long r){
    t[rt].tag_x = 1; t[rt].tag = 0;//初始化
    t[rt].l = l,t[rt].r = r;//建立一个结点，更新左右端点标记 
    if(l == r){ //如果到了叶子结点 
        t[rt].sum = a[l] % p; //不要忘记取模操作 
        return;
    }
    long long mid = (l + r) >> 1; //中间节点 
    build(ls(rt),l,mid);
    build(rs(rt),mid+1,r); //如果不是叶子结点，就分别建立左右孩子 
    t[rt].sum = (t[ls(rt)].sum + t[rs(rt)].sum) % p; // 更新sum 
}

区间修改（划重点）

• 懒标记 lazy_tag

  这个题来讲，我们的加减、乘除都是区间修改操作，如果将线段树拆开在每个叶子结点上面进行修改再维护，最坏情况下我们修改的复杂度就变成了O(mnlogn)，比暴力还慢。

我们引入懒标记lazy_tag。每一个线段树的结点都会有一个加法的tag和乘法的tag_x，如果我们想要修改的区间覆盖了结点的对应区间，我们不对其中的每一个元素进行修改，而是只更新tag、tag_x和sum，这样就巧妙地优化了程序的复杂度。

x长得很像乘号，所以tag_x就是乘法的懒标记（特别有道理对吧）。

当然，我们的懒标记也需要在访问的时候，对一个结点进行更新，即把父亲节点（rt）的tag下传到儿子节点，同时更新儿子的sum。如果只有加法这个事情就简单了，可是现在我萌有了乘法，那就要考虑一下运算顺序的问题了。因为乘法的运算级别更高，所以先进行计算。 注意：乘法懒标记不仅要把sum改成sum * tag_x，而且，加法的懒标记tag也要改成tag * tag_x，因为加法tag也是sum的一部分。 另外，因为牵扯到tag会发生变化，代码里面修改的语句也有一定的顺序（tag_x高于tag，tag高于sum）。这一套操作叫懒标记下传。

void push_down(long long rt){
    t[ls(rt)].tag_x = (t[ls(rt)].tag_x * t[rt].tag_x) % p;
    t[rs(rt)].tag_x = (t[rs(rt)].tag_x * t[rt].tag_x) % p;//乘法懒标记更新后取模 

    t[ls(rt)].tag = (t[ls(rt)].tag * t[rt].tag_x) % p;
    t[rs(rt)].tag = (t[rs(rt)].tag * t[rt].tag_x) % p;//加法懒标记更新 

    t[ls(rt)].sum = (t[ls(rt)].sum * t[rt].tag_x) % p;
    t[rs(rt)].sum = (t[rs(rt)].sum * t[rt].tag_x) % p;//sum结点对应区间和更新

    t[rt].tag_x = 1; //父亲的标记已经下传，就归零（因为是乘法，所以要调到1） 
        
    t[ls(rt)].tag = (t[ls(rt)].tag + t[rt].tag) % p;
    t[rs(rt)].tag = (t[rs(rt)].tag + t[rt].tag) % p;//加法懒标记更新 
    
    t[ls(rt)].sum += (t[ls(rt)].r - t[ls(rt)].l + 1) * t[rt].tag;
    t[rs(rt)].sum += (t[rs(rt)].r - t[rs(rt)].l + 1) * t[rt].tag;//sum结点对应区间和更新
    
    t[rt].tag = 0;//父亲的标记已经下传，就归零 
}

• 正题：区间修改

  懒标记看明白，区间修改就简单了。我萌从第一个结点开始，判断要进行修改的区间是不是覆盖了这个结点的区间，如果覆盖，直接一套骚操作把这个点的tag、tag_x和sum改掉。如果没有覆盖，就往这个节点的孩子递归，直到找到被覆盖的区间。
  这里分加法和乘法的区间修改，但是思路相同。还是需要注意一下tag和tag_x的修改顺序。

加法

void change(long long rt,long long x,long long y,long long z){
    if(x <= t[rt].l && y >= t[rt].r){
        t[rt].tag = (t[rt].tag + z) % p;
        t[rt].sum = (t[rt].sum + (t[rt].r - t[rt].l + 1) * z) % p; //如果修改区间覆盖了这个节点的区间，就更新 
        return;
    }
    if(t[rt].tag || t[rt].tag_x != 1) push_down(rt);//访问孩子结点的时候一定先把懒标记 传下去 
    long long mid = (t[rt].l + t[rt].r) >> 1;
    if(x <= mid){
        change(ls(rt),x,y,z);
    }
    if(y > mid){
        change(rs(rt),x,y,z);
    }
    //分别往左右儿子传 
    
    t[rt].sum = (t[ls(rt)].sum + t[rs(rt)].sum) % p; //维护 
}

乘法

void change_x(long long rt,long long x,long long y,long long z){
     if(x <= t[rt].l && y >= t[rt].r){
        t[rt].tag_x = (t[rt].tag_x * z) % p;
        t[rt].sum = (t[rt].sum * z) % p;
        t[rt].tag = (t[rt].tag * z) % p;//如果修改区间覆盖了这个节点的区间，就更新 
        return;
     }
     if(t[rt].tag || t[rt].tag_x != 1) push_down(rt);//访问孩子结点的时候一定先把懒标记 传下去 
     long long mid = (t[rt].l + t[rt].r) >> 1;
     if(x <= mid){
        change_x(ls(rt),x,y,z);
     }
     if(y > mid){
        change_x(rs(rt),x,y,z);
     }
     //分别往左右儿子传 
     t[rt].sum = (t[ls(rt)].sum + t[rs(rt)].sum) % p; //维护
}

区间查询

思路和区间修改相类似，从第一个结点开始 ，如果结点被覆盖，就返回它维护的区间和sum。

long long getsum(long long rt,long long x,long long y){
    long long res = 0;
    if(x <= t[rt].l && y >= t[rt].r){
        return t[rt].sum % p;
    }
    if(t[rt].tag || t[rt].tag_x != 1) push_down(rt);
    long long mid = (t[rt].r + t[rt].l) >> 1;
    if(x <= mid){
        res += getsum(ls(rt),x,y);
    }
    if(y > mid){
        res += getsum(rs(rt),x,y);
    }
    return res % p;
}

讲到这里，线段树就结束啦（跑回去纠错ing）

来一波AC代码

（注释掉的部分是线段树1的代码，两个题基本上一样的，就写到一块了）

#include "bits/stdc++.h"
#define N 1000000+50
using namespace std;

struct tree{
    long long l,r,sum,tag,tag_x;//l,r左右端点，sum为结点对应区间和，tag为加法标记，tag_x为乘法标记 
}t[N];//线段树 
long long a[N];//输入的数列(1~n) 
long long m,n,p = 9223372036854775807,k;//如题意(k是操作种类) 
long long ls(long long rt){return rt<<1;}//左孩子 
long long rs(long long rt){return rt<<1|1;}//右孩子 

void build(long long rt,long long l,long long r){
    t[rt].tag_x = 1; t[rt].tag = 0;//初始化
    t[rt].l = l,t[rt].r = r;//建立一个结点，更新左右端点标记 
    if(l == r){ //如果到了叶子结点 
        t[rt].sum = a[l] % p; //不要忘记取模操作 
        return;
    }
    long long mid = (l + r) >> 1; //中间节点 
    build(ls(rt),l,mid);
    build(rs(rt),mid+1,r); //如果不是叶子结点，就分别建立左右孩子 
    t[rt].sum = (t[ls(rt)].sum + t[rs(rt)].sum) % p; // 更新sum 
}

void push_down(long long rt){
    t[ls(rt)].tag_x = (t[ls(rt)].tag_x * t[rt].tag_x) % p;
    t[rs(rt)].tag_x = (t[rs(rt)].tag_x * t[rt].tag_x) % p;//乘法懒标记更新后取模 

    t[ls(rt)].tag = (t[ls(rt)].tag * t[rt].tag_x) % p;
    t[rs(rt)].tag = (t[rs(rt)].tag * t[rt].tag_x) % p;//加法懒标记更新 

    t[ls(rt)].sum = (t[ls(rt)].sum * t[rt].tag_x) % p;
    t[rs(rt)].sum = (t[rs(rt)].sum * t[rt].tag_x) % p;//sum结点对应区间和更新

    t[rt].tag_x = 1; //父亲的标记已经下传，就归零（因为是乘法，所以要调到1） 
        
    t[ls(rt)].tag = (t[ls(rt)].tag + t[rt].tag) % p;
    t[rs(rt)].tag = (t[rs(rt)].tag + t[rt].tag) % p;//加法懒标记更新 
    
    t[ls(rt)].sum += (t[ls(rt)].r - t[ls(rt)].l + 1) * t[rt].tag;
    t[rs(rt)].sum += (t[rs(rt)].r - t[rs(rt)].l + 1) * t[rt].tag;//sum结点对应区间和更新
    
    t[rt].tag = 0;//父亲的标记已经下传，就归零 
}

void change(long long rt,long long x,long long y,long long z){
    if(x <= t[rt].l && y >= t[rt].r){
        t[rt].tag = (t[rt].tag + z) % p;
        t[rt].sum = (t[rt].sum + (t[rt].r - t[rt].l + 1) * z) % p; //如果修改区间覆盖了这个节点的区间，就更新 
        return;
    }
    if(t[rt].tag || t[rt].tag_x != 1) push_down(rt);//访问孩子结点的时候一定先把懒标记 传下去 
    long long mid = (t[rt].l + t[rt].r) >> 1;
    if(x <= mid){
        change(ls(rt),x,y,z);
    }
    if(y > mid){
        change(rs(rt),x,y,z);
    }
    //分别往左右儿子传 
    
    t[rt].sum = (t[ls(rt)].sum + t[rs(rt)].sum) % p; //维护 
}

void change_x(long long rt,long long x,long long y,long long z){
     if(x <= t[rt].l && y >= t[rt].r){
        t[rt].tag_x = (t[rt].tag_x * z) % p;
        t[rt].sum = (t[rt].sum * z) % p;
        t[rt].tag = (t[rt].tag * z) % p;//如果修改区间覆盖了这个节点的区间，就更新 
        return;
     }
     if(t[rt].tag || t[rt].tag_x != 1) push_down(rt);//访问孩子结点的时候一定先把懒标记 传下去 
     long long mid = (t[rt].l + t[rt].r) >> 1;
     if(x <= mid){
        change_x(ls(rt),x,y,z);
     }
     if(y > mid){
        change_x(rs(rt),x,y,z);
     }
     //分别往左右儿子传 
     t[rt].sum = (t[ls(rt)].sum + t[rs(rt)].sum) % p; //维护
}

long long getsum(long long rt,long long x,long long y){
    long long res = 0;
    if(x <= t[rt].l && y >= t[rt].r){
        return t[rt].sum % p;
    }
    if(t[rt].tag || t[rt].tag_x != 1) push_down(rt);
    long long mid = (t[rt].r + t[rt].l) >> 1;
    if(x <= mid){
        res += getsum(ls(rt),x,y);
    }
    if(y > mid){
        res += getsum(rs(rt),x,y);
    }
    return res % p;
}

int main(){
    long long i,j,x,y,z;
    scanf("%lld%lld%lld",&n,&m,&p);
//    scanf("%lld%lld",&n,&m); 
    for(i = 1;i <= n; i++){
         scanf("%lld",&a[i]);
    }
    build(1,1,n);
    for(i = 1;i <= m; i++){
        scanf("%lld",&k);
        
        if(k == 1){
            scanf("%lld%lld%lld",&x,&y,&z);
            change_x(1,x,y,z);
        }else if(k == 2){
            scanf("%lld%lld%lld",&x,&y,&z);
            change(1,x,y,z);
        }else if(k == 3){
            scanf("%lld%lld",&x,&y);
            printf("%lld
",getsum(1,x,y));
        }

//      if(k == 1){
//          scanf("%lld%lld%lld",&x,&y,&z);
//          change(1,x,y,z);
//      }else if(k == 2){
//          scanf("%lld%lld",&x,&y);
//          printf("%lld
",getsum(1,x,y));
//      }
        
    }
    return 0;
}