数据结构算法及线性表总结
Posted 22225942w
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了数据结构算法及线性表总结相关的知识,希望对你有一定的参考价值。
一、思维导图
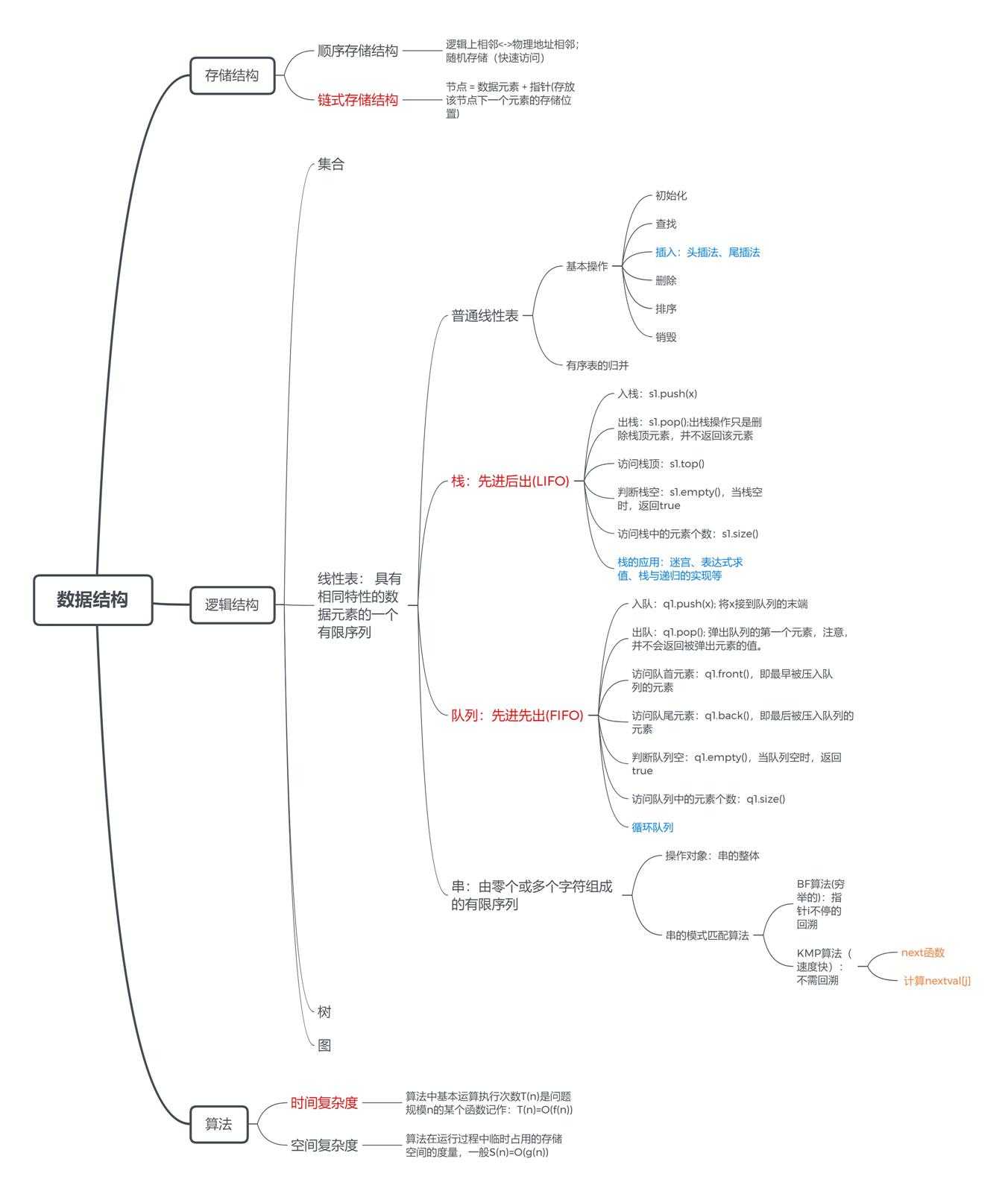
二、重要概念
1.算法
(1)时间复杂度的计算
2.线性表
(1)头插法建立单链表:建立的表格元素顺序与输入元素顺序相反
void CreateListF(LinkList& L, int n)//头插法建链表,L表示带头结点链表,n表示数据元素个数
{
int i;
LinkList p;
L = new LNode;
L->next = NULL;
for (i = 0; i < n; i++) {
p = new LNode;
cin >> p->data;
p->next = L->next;
L->next = p;
}
}
(2)尾插法建立单链表
void CreateListR(LinkList& L, int n)//尾插法建链表,L表示带头结点链表,n表示数据元素个数
{
int i;
LinkList head, p;
L = new LNode;
head = L;
for (i = 0; i < n; i++) {
p = new LNode;
cin >> p->data;
head->next = p;
head = p;
}
head->next = NULL;
}
3.栈和队列
(1)Stack
栈的进栈出栈规则:
? 按序进栈→有n个元素1,2,…,n,它们按1,2, …,n的次序进栈(i进栈时, 1~(i-1)应该已进栈);栈顶元素先出栈→栈底元素最后出栈;
? 时进时出→元素未完全进栈时,即可出栈。
栈在算法中的作用: 暂存程序运行的中间状态
后缀表达式:运算符号位于两个运算数之后
递归:一个直接调用自己或通过一系列的调用语句间接地调用自己的函数
特点:自我调用 、必须有递归出口
(2)queue
队尾(rear)——允许插入的一端
队头(front)——允许删除的一端
循环队列:数组首尾相接
入/出队列运算,利用“模运算”,则:
?入队:Q.rear=(Q.rear+1)%m
?出队:Q.front=(Q.front+1)%m
队满和队空判断条件:
1.另外设一个标志以区别队空、队满
2.少用一个元素空间:
队空:Q.rear = Q.front
队满:(Q.rear+1) % m = Q.front
4.串
(1)BF算法:
将目标串S的第一个字符与模式串T的第一个字符进行匹配,若相等,则继续比较S的第二个字符和 T的第二个字符;若不相等,则比较S的第二个字符和T的第一个字符,依次比较下去,直到得出最后的匹配结果
一般情况下:此算法的时间复杂度为O(n+m);最坏情况下:时间复杂度为O(n×m) !
(2)KMP算法:主串不需回溯i指针;将模式串向右“滑动”尽可能远的一段距离
next[j]函数:
当j从1开始,next[1]=0,next[j]=k,k=1+length(最大的前缀串与后缀串相等长度),其他情况next[j]=1;当j从0开始,next[0]=-1,next[1]=0,next[j]=k,k=length(最大的前缀串与后缀串相等长度)
void get_next(SString &T, int &next[] ) { // 求模式串T的next函数值并存入数组next
i = 1; next[1] = 0; j = 0;
while (i < T[0]) {
if (j = 0 || T[i] == T[j])
{++i; ++j; next[i] = j; }
else j = next[j];
}
} //get_next
nextval[j]函数:
可根据next[j]函数计算
void get_nextval(SString &T, int &nextval[])
{
i = 1; nextval[1] = 0; j = 0;
while (i < T[0]) {
if (j=0 || T[i]==T[j]) {
++i; ++j;
if (T[i] != T[j]) nextval[i] = j;
else nextval[i] = nextval[j];
}
else j = nextval[j];
}
} // get_nextval
四、疑难问题及解决方案
1、计算nextval[j]
解决方案:先计算出next[j]函数
如:ababa,nextval[1]=0,nextval[2]=1,j=3时,由于T[i]的元素之前出现过,next[3]=1,所以找到next[1]的值,若T[1]=T[3]则该值就是nextval[3]的值

2、银行业务队列简单模拟(还在解决中)
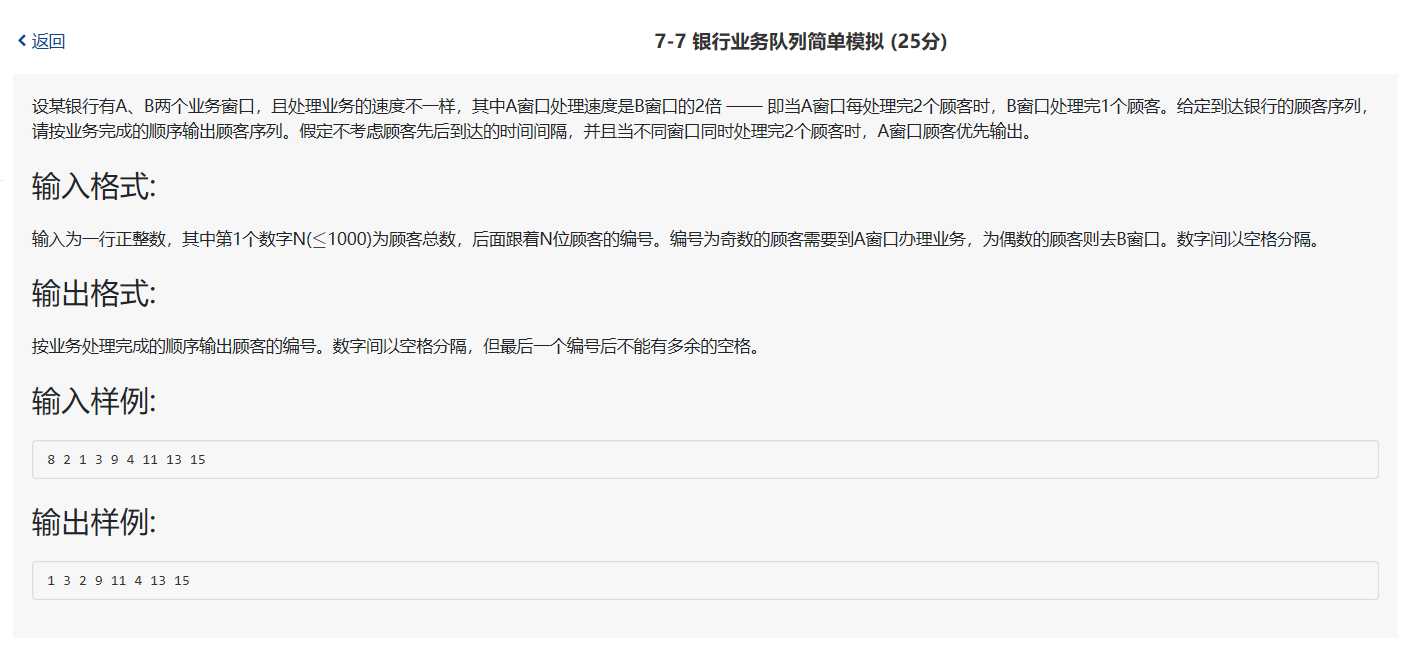
#include<iostream>
#include<queue>
using namespace std;
int main()
{
int i, n, x;
queue<int>A, B;
cin >> n;
for (i = 0; i < n; i++) {
cin >> x;
if (x % 2 == 0)B.push(x);
else A.push(x);
}
if (n == 1)cout << x;
else if (A.size() >= B.size()) {
for (i = 0; i < n; i++) {
if (!A.empty()) { cout << A.front(); A.pop(); }
if (!A.empty()) {
cout << " " << A.front(); A.pop();
}
if (!B.empty()) {
cout << " " << B.front() << " "; B.pop();
}
i = i + 2;
}
}
else if (B.size()> A.size()) {
for (i = 0; i < A.size();i++) {
if (!A.empty()) { cout << A.front(); A.pop(); }
if (!A.empty()) {
cout << " " << A.front(); A.pop();
}
if (!B.empty()) {
cout << " " << B.front()<<" "; B.pop();
}
i = i + 2;
}
for (i = 0; !B.empty(); i++) {
cout << B.front() << " ";
B.pop();
}
}
return 0;
}
结果:
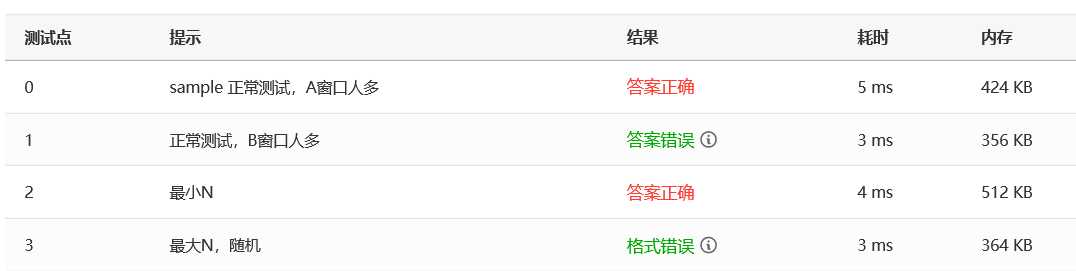
以上是关于数据结构算法及线性表总结的主要内容,如果未能解决你的问题,请参考以下文章