求解最大连续子数组和问题

Posted 2021-02-10

前言

最近工作不是特别忙，所以有更多时间来学习算法相关知识，补短处。题目来源于leetcode，通过一个算法题，我们去分析该算法题所属类型，以及解题思路，以及该算法题所用到的数学知识。选择的算法题目从容易到困难，逐步提高难度，解题的思路也是从简单到复杂，时间复杂度也是从低到高的顺序来书写这个系列的博客。因工作语言和使用熟练度原因算法采用Java编写，但该系列中可能会穿插c、C++、python语言实现，请不要奇怪。

题目

分析题目：给定的整型数组，求解最大连续子数组和，要求是至少包含一个元素，且算法时间复杂度至少O(n).
首先我们想到就是：计算所有子数组的和进行比较取最大值，该方式叫做暴力求解，如果在数据规模很小的情况下我们就可以很轻松的接触结果，但一旦 规模稍微大一些，其性能就及其低了。那么我们先来写一下暴力求解算法实现。

暴力求解算法

    // 1.暴力解析
    private static int maxSubArrayByVoilence(int[] nums) {
        if(nums.length == 1){
            return nums[0];
        }
        int currentSubSum,maxSubSum=nums[0];
        // 思路: 1.暴力破解。遍历子数组的和进行比较
        for(int i =0; i < nums.length; i++){
            for (int j = i; j < nums.length; j++){
                // 当前子数组和
                currentSubSum = 0;
                for (int k = i; k <= j; k++){
                    currentSubSum += nums[k];
                }
                // 比较最大值与当前子数组和
                if(currentSubSum>maxSubSum){
                    maxSubSum = currentSubSum;
                }
            }
        }
        return maxSubSum;
    }

分析：该解题方法的时间复杂度为O(n^3).效率非常低，但逻辑非常简单。针对暴力破解算法，我们可以考虑进行优化，使其时间复杂度降低为O(n^2),因为简单所以不再这里多写，同时也留给读者自行编写，如果可以你可以留言下来给其他读者或者给我看，看看你的优化思路。

最大连续子数组问题让我想到了《数据结构与算法》中的一个名词：最优解问题。该类问题就是属于最优解类型的题目，所以我们可以通过最优解问题的解题思路来解决这个算法题目：动态规划算法。

动态规划算法

动态规划算法-百度词条
动态规划算法的基本思想与分治法类似，也是将待求解的问题分解为若干个子问题（阶段），按顺序求解子阶段，前一子问题的解，为后一子问题的求解提供了有用的信息。在求解任一子问题时，列出各种可能的局部解，通过决策保留那些有可能达到最优的局部解，丢弃其他局部解。依次解决各子问题，最后一个子问题就是初始问题的解。
由于动态规划解决的问题多数有重叠子问题这个特点，为减少重复计算，对每一个子问题只解一次，将其不同阶段的不同状态保存在一个二维数组中。

上面是百度词条的解释，理解起来不难，那么我们这个问题，该如何实现算法呢？废话不多说，代码先撸出来。

    // 3.动态规划
    private static int maxSubArrayByDP(int[] nums) {
        if(nums.length == 1){
            return nums[0];
        }
        int maxSubSum = nums[0],currentSubSum = nums[0];
        for(int i=1;i<nums.length;i++){
            currentSubSum += nums[i];
            // 如果加上nums[i]后反而更小了，则从nums[i]开始重新计算
            if(currentSubSum < nums[i]){
                currentSubSum = nums[i];
            }
            // 比较大小
            if(currentSubSum > maxSubSum){
                maxSubSum = currentSubSum;
            }
        }
        return maxSubSum;
    }

分析：动态规划算法时间复杂度为O(n),相比较于暴力解法效率就大大提升了。关键点在于如果加上nums[i]后相比较nums[i]小，那么说明i之前和比i数值小，所以既然比之前小，那么就可以把前面的都抛开重新规划计算和。
动态规划的数学表达：currentSubSum(i)表示数组下标以i为起点的最大连续下标最大的和，而maxsum(i)表示前i个元素的最大子数组之和。那么我们就可以推出下一个maxsum(i+1)应该为cursum(i+1)和maxsum(i)中选取一个最大值。递推式为：
currentSubSum(i) = max{A[i],currentSubSum(i-1)+A[i]};
maxSubSum(i) = max{maxsum(i-1),currentSubSum(i+1)};

根据follow up的说明，还可以使用分治法去求解这个算法题。那么我们接下来看看分治法如何实现这个算法。

分治算法

// 4.分治算法+递归
    private static int maxSubArrayByDC(int[] num, int low, int high) throws Exception {
        // 终止条件
        if(low==high)
            return num[low];
        else if(low<high)
        {
            int mid = (low+high)/2;
            // 左侧最大子数组和计算
            int left = maxSubArrayByDC(num,low,mid);
            // 右侧最大子数组和计算
            int right = maxSubArrayByDC(num,mid+1,high);
            // 跨越分区子数组和计算
            int sum=0,max=0,i=0,j=0,center=0;
            for(i=mid;i>=low;i--)
            {
                sum+=num[i];
                if(sum>max)
                {
                    max = sum;
                }
            }
            center+=max;
            max = -1;
            sum=0;
            for(j=mid+1;j<=high;j++)
            {
                sum+=num[j];
                if(sum>max)
                {
                    max = sum;
                }
            }
            center+=max;
            j = left>=right?left:right;
            j = j>=center?j:center;
            return j;
        }else {
            // 抛出异常
            throw new Exception("索引值错误，low值一定不能比high值大");
        }
    }

分析:分治法处理规模大的问题时，采用的是缩小规模，然后比较各个规模的结果，从而得出最终结果。分治法的时间复杂度为O(nlogn)这里关键是理解分治思想，对于分治思想，我从网上找了一张图片，如下，能够很好的帮助我们理解和记住这种思维方式。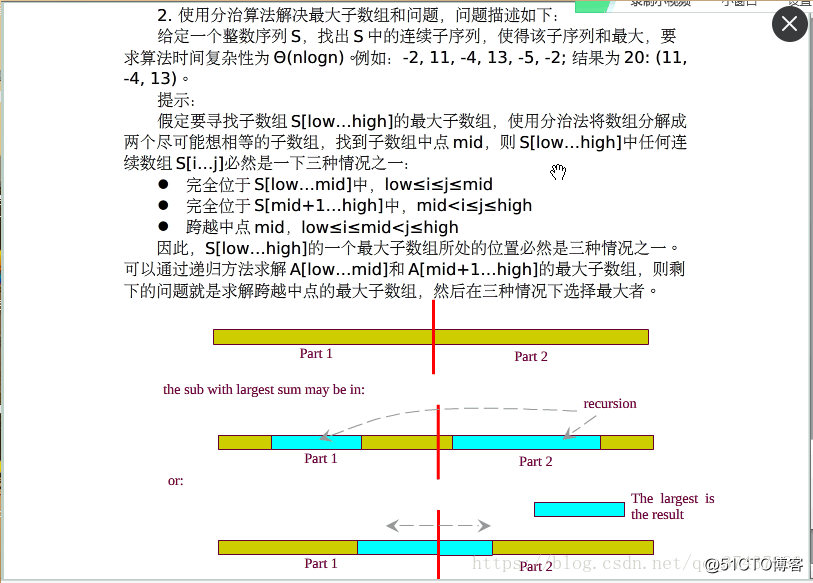

总结

该算法题虽然是很简单的一道题目，但包含的算法思想非常优秀。该系列的文章，我会陆续的写一些题目的解法，但不会所有LeetCode题目都写，我选择题目的要求是：有意思（包括多种有意思的解题算法，或者我不懂的算法）的，有技巧的，有深度的。如果你对这题有更多想说的可以在下面留言和读者讨论，我也会一起参与的哟。