DS树+图综合练习--二叉树之最大路径

Posted 2021-02-01 liu269393

题目描述

给定一颗二叉树的逻辑结构（先序遍历的结果，空树用字符‘0’表示，例如AB0C00D00），建立该二叉树的二叉链式存储结构

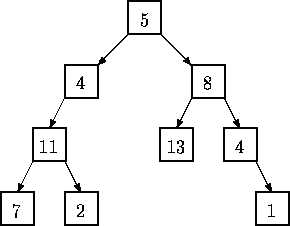
二叉树的每个结点都有一个权值，从根结点到每个叶子结点将形成一条路径，每条路径的权值等于路径上所有结点的权值和。编程求出二叉树的最大路径权值。如下图所示，共有4个叶子即有4条路径，

路径1权值=5 + 4 + 11 + 7 = 27          路径2权值=5 + 4 + 11 + 2 = 22

路径3权值=5 + 8 + 13 = 26                路径4权值=5 + 8 + 4 + 1 = 18

可计算出最大路径权值是27。

该树输入的先序遍历结果为ABCD00E000FG00H0I00，各结点权值为：

A-5，B-4，C-11，D-7，E-2，F-8，G-13，H-4，I-1

 

 

输入

第一行输入一个整数t，表示有t个测试数据

第二行输入一棵二叉树的先序遍历，每个结点用字母表示

第三行先输入n表示二叉树的结点数量，然后输入每个结点的权值，权值顺序与前面结点输入顺序对应

以此类推输入下一棵二叉树

输出

每行输出每棵二叉树的最大路径权值，如果最大路径权值有重复，只输出1个

样例输入

2

AB0C00D00

4 5 3 2 6

ABCD00E000FG00H0I00

9 5 4 11 7 2 8 13 4 1

样例输出

11

27

这里只需给每个树节点添加属性weight即可，在创建树的时候每次传入父节点的weight，孩子节点迭代相加即可，并在类中设置属性maxleaveweight来记录叶子节点的最大权值，在创建树的时候就可以判断了，不需要再次调用任何一种遍历来设置maxleaveweigth

#include<iostream>
#include<string>
using namespace std;
class BitreeNode
{
public:
    char data;
    int weight;
    int hight;
    BitreeNode *left;
    BitreeNode *right;
    BitreeNode() :hight(0),weight(0),left(NULL), right(NULL) {}
    ~BitreeNode() {}
};
class Bitree
{
private:
    BitreeNode *Root;
    int pos,po;    
    string strtree;
    BitreeNode *CreateBitree(int w[],int fatherweight);
    void preorder(BitreeNode *t);
public:
    int maxleaveweight;
    Bitree() { maxleaveweight = 0; };
    ~Bitree() {};
    void CreateTree(string TreeArray,int w[]);
    void preorder();
};
void Bitree::CreateTree(string treearray,int w[])
{
    pos = 0;
    po = 0;
    strtree.assign(treearray);
    Root = CreateBitree(w,0);
}
BitreeNode *Bitree::CreateBitree(int w[],int fatherweight)
{
    BitreeNode *T;
    char ch;
    ch = strtree[pos++];
    if (ch == ‘0‘)
        T = NULL;
    else
    {
        T = new BitreeNode();
        T->data = ch;
        T->weight = w[po++]+fatherweight;
        if (!T->left && !T->right)
            if (T->weight > maxleaveweight)
                maxleaveweight = T->weight;
        T->left = CreateBitree(w,T->weight);
        T->right = CreateBitree(w,T->weight);
    }
    return T;
}
void Bitree::preorder()
{
    preorder(Root);
    cout << maxleaveweight << endl;
}
void Bitree::preorder(BitreeNode *t)
{
    if (t)
    {
        if (!t->left && !t->right)
            if (t->weight > maxleaveweight)
                maxleaveweight = t->weight;
        preorder(t->left);
        preorder(t->right);
    }
}
int main()
{
    int t;
    cin >> t;
    while (t--)
    {
        string str;
        cin >> str;
        Bitree *tree;
        int n,*w;
        cin >> n;
        w = new int[n];
        for (int i = 0; i < n; i++)
            cin >> w[i];
        tree = new Bitree();
        tree->CreateTree(str,w);
        cout << tree->maxleaveweight << endl;
    }
}