DP Training（Updating）?(^?^*)

Posted 2021-01-11 wawawa8

DP Training

DP Training 01

https://vjudge.net/contest/220286 密码 nfls

A 数塔（Easy）

(f[i][j]) 表示当前选第 (i) 行，第 (j) 列的格子，上面的选完了，下面的没选的最大方案

(f[i][j]=max(f[i-1][j-1],f[i-1][j])+a[i][j])

B 数塔（Medium）

不难发现答案一定是交点到四个顶点的最大路径之和，预处理 (f[4][i][j]) 表示 ((i,j)) 到四个定点的最优距离，然后枚举交点计算结果

注意有两种情况：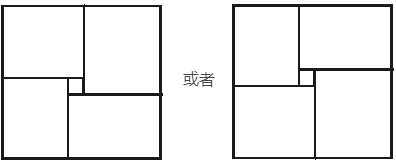

分别统计答案即可

C 数塔（Hard）

题目坏掉了

写了一个不知道真的假的

我们把来回想象成两个人一起从左上角走到右下角， (f[i][j][k]) 表示当前走到第 (i) 行，第一个人在第 (j) 列，第二个人在第 (k) 列，最大收益，转移的时候枚举第一个人是否是从左边来的，第二个人是否是从左边来的（否则就是从上边来的），复杂度 (O(n^3))

D 最大连续和（Easy）

这个好像不用( ext{dp})，直接维护一个当前的和以及当前的和对应的左端点

每次如果当前和>=0，那么就加上现在这个数，否则当前和改成现在这个数，左端点改成现在的位置（显然前面的负数没有意义）

rep(i,1,n){
    if(nw>=0 && nwl) nw+=a[i];
    else nwl=i,nw=a[i];
   if(nw>ans){ans=nw;ansl=nwl;ansr=i;}
}

E 最大连续和（Medium）

跟D一样的做法

首先枚举左边界和右边界，然后就把二维问题转化成了一维问题，每一个数就是对应的行的左边界与右边界之间数的和，然后用上面的方法求一下最大连续和即可，复杂度 (O(n^3))

F 最大连续和（Hard）

垃圾题目

一眼看上去不可做，网上翻一下题解，复杂度 (O(nm)) ？题目中根本没有说明 (m) 的范围，我以为 (m) 可以达到(1 ext{e}6)……

然后就好做了，想怎么做怎么做

先记一个 (f[i][j]) 表示当前选到第 (i) 个数，当前选了 (j) 段，最大的收益

转移就是
[f[i][j]=MAX(f[i-1][j],MAX_{0 le k lt i}{f[k][j-1]})+a[i]]

然后记录一个前缀MAX就可以做到 (O(nm)) 了，注意空间需要滚动数组优化