函数的奇偶性初级和中阶辅导

Posted 2021-01-10 wanghai0666

一、函数奇偶性还可能以什么形式给出？

1、直接给出；

如函数(f(x))在某区间(D)上是奇函数。

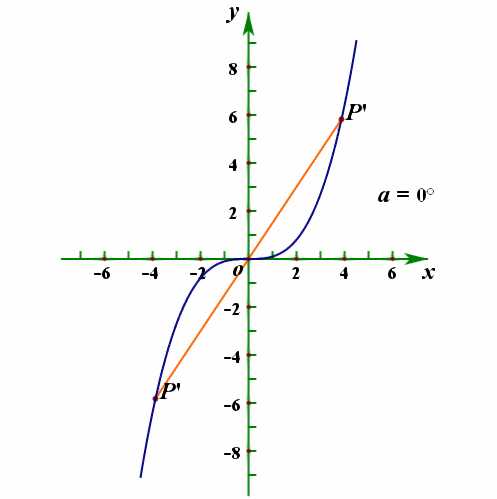
2、以定义式给出；

如(forall x in D，f(-x)= - f(x))，则它是奇函数。如函数(f(x)=x^3)，

3、定义的变形式给出；

如(forall x in D，f(-x)+ f(x)=0)，(cfrac{f(-x)}{f(x)}=pm 1(f(x) eq0)).

【应用①】

比如函数(f(x)=ln(sqrt{x^2+1}-x))，

则可知(f(-x)=ln(sqrt{x^2+1}+x))，

即(f(x)+f(-x)=ln1=0)，即函数(f(x))为奇函数；

那么函数(f(x)=ln(sqrt{x^2+1}-x)+1)呢?

同理可得，(f(x)+f(-x)=2)，

即函数(f(x))关于点((0，1))对称。

【应用②】

比如函数(g(x)=lg(sqrt{sin^2x+1}+sinx))，

则可知(g(-x)=lg(sqrt{sin^2x+1}-sinx))，

即(g(x)+g(-x)=lg1=0)，即函数(g(x))为奇函数；

4、以图像的形式给出；

比如某函数图像关于原点对称，某函数图像关于(y)轴对称。

5、以奇偶性的性质应用的结论形式给出；

在公共定义域上，以下结论是成立的，也是可以证明的；

(“奇+奇”)是奇，

如(f(x)=x+sinx)；(g(x)=x^3+2sinx)；(h(x)=x+cfrac{1}{x})；(h(x)=2x+cfrac{3}{x})；

(“奇-奇”)是奇，

如(f(x)=x^3-sinx)；(h(x)=x-cfrac{2}{x})；

(“奇cdot奇”)是偶，

如(f(x)=xcdot sinx)；(f(x)=x^3sinx)；

(“奇÷奇”)是偶；

如(f(x)=cfrac{sinx}{x})；

(“偶+偶”)是偶，(“偶-偶”)是偶；
(“偶cdot 偶”)是偶，(“偶÷偶”)是偶；
(“奇cdot偶”)是奇，(“奇÷偶”)是奇；

如(f(x))为偶函数，则可知函数(g(x)=xf(x))为奇函数。

• 特例，原来没有奇偶性的函数，进行四则运算后，又有了奇偶性。

如(f(x)=e^x+cfrac{1}{e^x}=e^x+e^{-x})，偶函数；

如(f(x)=e^x-cfrac{1}{e^x}=e^x-e^{-x})，奇函数；

补充简单的证明模式，
已知$f(x)、g(x)$都是奇函数，证明$H(x)=f(x)+g(x)$为奇函数；
分析：$f(x)、g(x)$都是奇函数，则函数$H(x)$的定义域必关于原点对称，
且满足$f(-x)=-f(x)$，$g(-x)=-g(x)$，
则$H(-x)=f(-x)+g(-x)=-[f(x)+g(x)]=-H(x)$，
故$H(x)$为奇函数。

6、以图像变换为依托给出，

如(f(x-1))的对称轴是(x=1)，则可知(f(x))的对称轴是(y)轴，即(f(x))是偶函数；

7、以周期性和对称性结合给出奇偶性；

已知函数(f(x))的周期是2，且满足(f(2+x)=f(-x))，则可推知函数(f(x))为偶函数。

具体变形如下：

由(f(x+2)=f(x))和(f(2+x)=f(-x))，

得到(f(-x)=f(x))，

故函数(f(x))为偶函数。

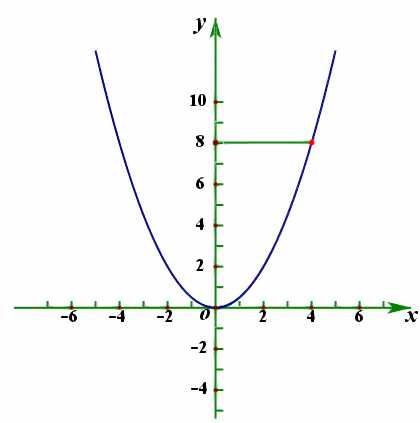
8、以结合赋值法给出；

已知函数(f(x))满足(f(1)=cfrac{1}{2})，且(f(x+y)+f(x-y)=2f(x)f(y))，则可推知函数(f(x))为偶函数。

具体变形如下：

令(x=y=0)，则有(2f(0)=2f^2(0))，得到(f(0)=0)或(f(0)=1)；

再令(x=1，y=0)，则有(2f(1)=2f(1)f(0))，得到(f(0)=1)；

又题目已知(f(1)=cfrac{1}{2})，得到(f(0)=1)[(f(0)=0)舍去]；

再令(x=0)，则得到(f(y)+f(-y)=2f(0)f(y)=2f(y))，

所以(f(-y)=f(y))，可知函数是偶函数。

9、以构造函数的形式给出或者得到奇偶性【难度大】；

具体例题请参见：例2

二、 函数的奇偶性的常用结论：

1、二次函数(y=ax^2+bx+c(a eq0)) 为偶函数的充要条件是(b=0) ，

证明：对称轴为(x=-cfrac{b}{2a})，

充分性：由(b=0)，得到对称轴为(x=0)，即就是(y)轴。

必要性：由函数为偶函数，对称轴是(x=-cfrac{b}{2a})， 得到(b=0)。

由此推广得到以下结论：

2、多项式函数(y=f(x)=ax^4+bx^3+cx^2+dx+e) 为奇函数的充要条件是(a=c=e=0)

说明： (f(-x)+f(x)=0)恒成立，

即([a(-x)^4+b(-x)^3+c(-x)^2+d(-x)+e]+(ax^4+bx^3+cx^2+dx+e))
(=2ax^4+2cx^2+2e=0)，

即(ax^4+cx^2+e=0)对(forall xin R)都成立，故(a=c=e=0)。

比如，已知函数(f(x)=x^3+(a-1)x^2+ax)为奇函数，则(a=1)；

3、多项式函数(y=ax^4+bx^3+cx^2+dx+e) 为偶函数的充要条件是(b=d=0)

仿上例可说明。

4、奇函数的导函数为偶函数；

文科：举例说明，比如函数(f(x)=sinx)为奇函数，其导函数为(f'(x)=cosx)为偶函数；

理科：逻辑证明，设函数(f(x))为奇函数，其导函数(f'(x))，

记(f'(x)=g(x))，由函数(f(x))为奇函数，

则有(f(-x)+f(x)=0)，对其两边求导得到，

(-f'(-x)+f'(x)=0)，即(-g(-x)+g(x)=0)，

即(g(-x)=g(x))，

即函数(g(x))为偶函数；

5、偶函数的导函数为奇函数；

文科：举例说明，比如函数(f(x)=cosx)为偶函数，其导函数为(f'(x)=-sinx)为奇函数；

理科：逻辑证明，设函数(f(x))为偶函数，其导函数为(f'(x))，

记(f'(x)=g(x))，由函数(f(x))为偶函数，

则有(f(-x)-f(x)=0)，对其两边求导得到，

(-f'(-x)-f'(x)=0)，即(-g(-x)-g(x)=0)，

即(g(-x)=-g(x))，

即函数(g(x))为奇函数；

6、若函数为奇函数，则在其关于原点对称的两点处的导函数的值相等。

文科：如(f(x)=x^3)，则(f'(x)=3x^2)，故(f'(-1)=f'(1)=3)；

理科：如函数(f(x))满足(f(-x)+f(x)=0)，则给两边求导得到，

(-f'(-x)+f'(x)=0)，则有(f'(x_0)-f'(-x_0)=0)

引申：对称性，若函数(f(x)+f(2-x)=2)，则函数(f(x))关于点((1，1))对称，

且(f'(x_0)=f'(2-x_0))，比如(f'(0)=f'(2))；

7、若函数为偶函数，则在其关于原点对称的两点处的导函数的值互为相反数。

文科：如(f(x)=x^2)，则(f'(x)=2x)，故(f'(-1)=-2，f'(1)=2)；

理科：如函数(f(x))满足(f(-x)-f(x)=0)，则给两边求导得到，

(-f'(-x)-f'(x)=0)，则有(f'(x_0)+f'(-x_0)=0)

引申：对称性，若函数(f(x)=f(2-x))，则函数(f(x))关于直线(x=1)对称，

且(f'(x_0)=-f'(2-x_0))，比如(f'(0)=-f'(2))；