怎样判断函数f（x）奇偶性？

Posted 2023-03-22

参考技术A

F(-x)=ln[-x+√(1+x²)]

=ln[-x+√(1+x²)][x+√(1+x²)]/[x+√(1+x²)] 分子有理化

=ln(1+x²-x²)/[x+√(1+x²)]

=ln1/[x+√(1+x²)]

=ln[x+√(1+x²)]^(-1)

=-ln[x+√(1+x²)]

=-F(x)

即F(-x)=-F(x)

所以F(x)是奇函数

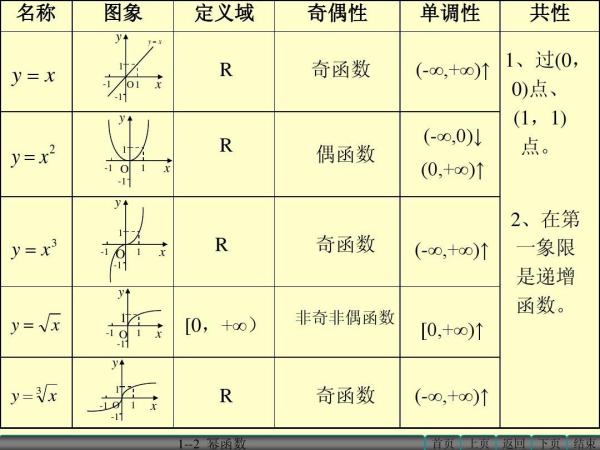
函数奇偶性特征：

偶函数：若对于定义域内的任意一个x，都有f(-x)=f(x)，那么f(x)称为偶函数。

奇函数：若对于定义域内的任意一个x，都有f(-x)=-f(x)，那么f(x)称为奇函数。

定理奇函数的图像关于原点成中心对称图表，偶函数的图象关于y轴成轴对称图形。

f(x)为奇函数《＝=》f(x)的图像关于原点对称

点（x，y）→（－x，－y）

奇函数在某一区间上单调递增，则在它的对称区间上也是单调递增。

偶函数在某一区间上单调递增，则在它的对称区间上单调递减。

判断函数y＝sinx＋x³的奇偶性？

如果你想判断函数y=sin(x)+x^3的奇偶性，你可以这样做：

首先，函数y=sin(x)+x^3是一个多项式函数，它的奇偶性取决于最高次幂的系数是否为奇数。在这个例子中，最高次幂的系数是1，所以函数y=sin(x)+x^3是奇函数。

你可以使用以下代码来判断函数y=sin(x)+x^3的奇偶性：

如果你想在更多的x值处判断函数的奇偶性，你可以使用循环来遍历所有的x值，例如：

参考技术A

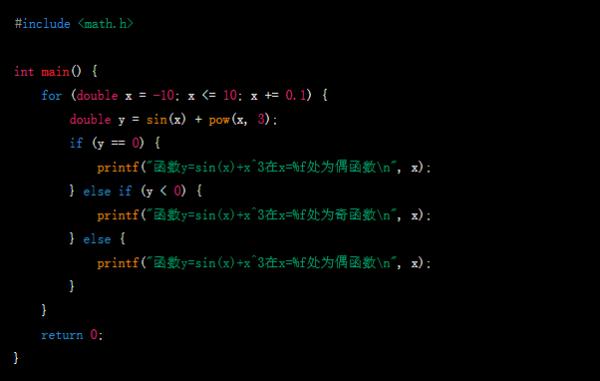
方法如下，请作参考：

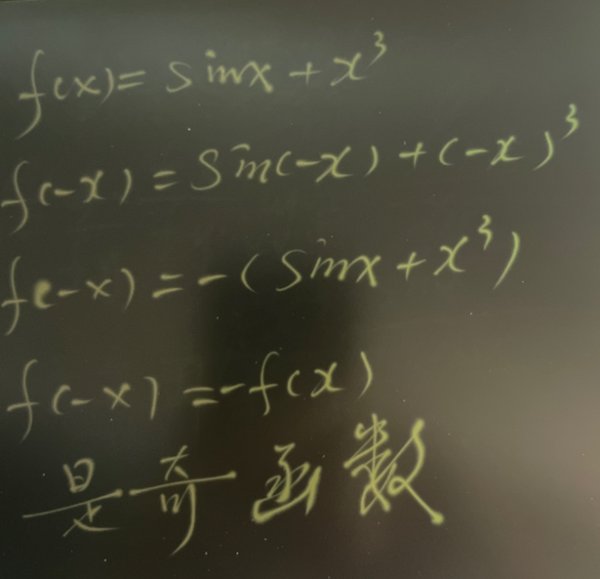
若有帮助，
请采纳。

参考技术B 函数y＝sinx＋x^3是奇函数。
解：函数y＝sinx＋x^3的定义域为（-∞，＋∞）；那么在x∈R中任意x，则-x∈R，得
f（-x）＝sin（-x）＋（-x）^3
＝-sinx-x^3
∴f（-x）＋f（x）＝sinx＋x^3＋（-sinx-x^3）＝0，即f（-x）＝-f（x）
∴y＝sinx＋x^3在x∈R中是奇函数。 参考技术C f（⁻x）=sin（-x）+（-x）³
=-sinx-x³
f（x）=-f（-x），即f（x）为奇函数 参考技术D f(x)=sinx＋x³
f(-x)=sin(-x)＋(-x)³=-sinx-x³=-(sinx＋x³)
∴f(-x)=-f(x)
∴f(x)=sinx＋x³是奇函数。