[数据结构] 哈夫曼树

Posted 2023-02-02 MAKISE004

哈夫曼树

哈夫曼树简介

给定 N 个权值作为 N 个叶子结点，构造一棵二叉树，若该树的带权路径长度达到最小，称这样的二叉树为最优二叉树，也称为哈夫曼树( Huffman Tree )。

哈夫曼树涉及的基本概念

路径和路径长度

在一棵树中，从一个结点往下可以达到的孩子结点之间的通路，称为路径。通路中分支的数目称为路径长度。若规定根结点的层数为1，则从根结点到第 L 层结点的路径长度为 L - 1 。

树的带权路径长度

设二叉树具有 n 个带权叶结点，从根结点到各叶结点的路径长度与相应叶节点权值的乘积之和称为 树的带权路径长度（Weighted Path Length of Tree，WPL ）。

设 w 为二叉树第 i 个叶结点的权值，l 为从根结点到第 i 个叶结点的路径长度，则 WPL 计算公式如下：

对于给定一组具有确定权值的叶结点，可以构造出不同的二叉树，其中，WPL 最小的二叉树称为哈夫曼树。
其叶结点权值越小，离根越远，叶结点权值越大，离根越近。

哈夫曼树的构建

哈夫曼树的构建思路

（1）将给定的 n 个节点构建成一个二叉树（初始情况下单个节点看成是一颗二叉树）的集合；
（2）每次在集合中选取最小权值的两个二叉树根节点，并将这两个二叉树将最小的一个作为左子树，次小的一个作为右子树，合并成一个新的二叉树；
（3）将取出的最小的两个二叉树从集合中删除，并将新的二叉树加入到集合中；
（4）重复步骤（2）、（3），最后集合中只剩下一个二叉树时，哈夫曼树构建完成。

构建哈夫曼树图解

（1）

初始化二叉树集合

（2）

最小的 1 和 3 合并为 4

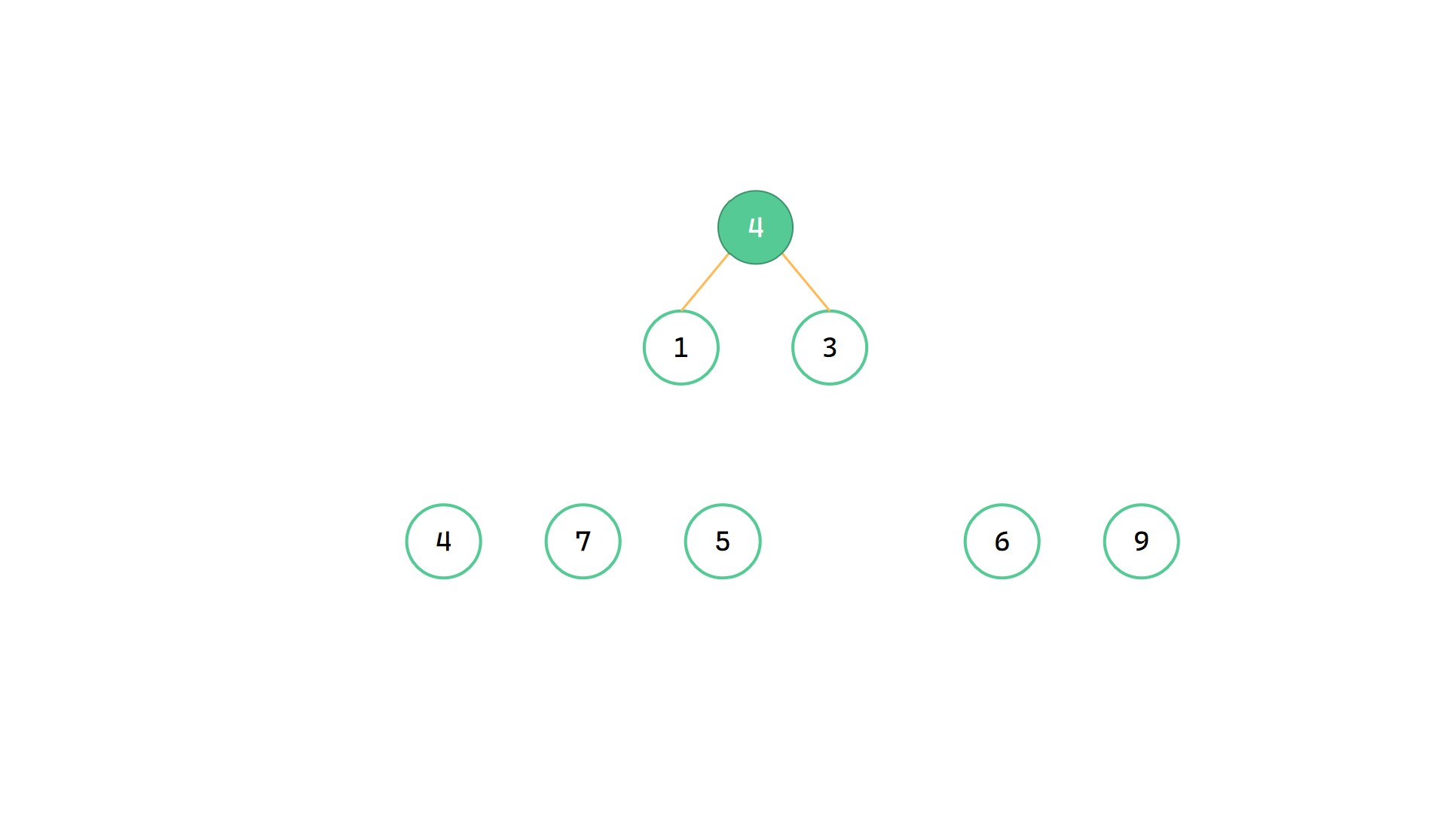
（3）

最小的 4 和 4 合并为 8

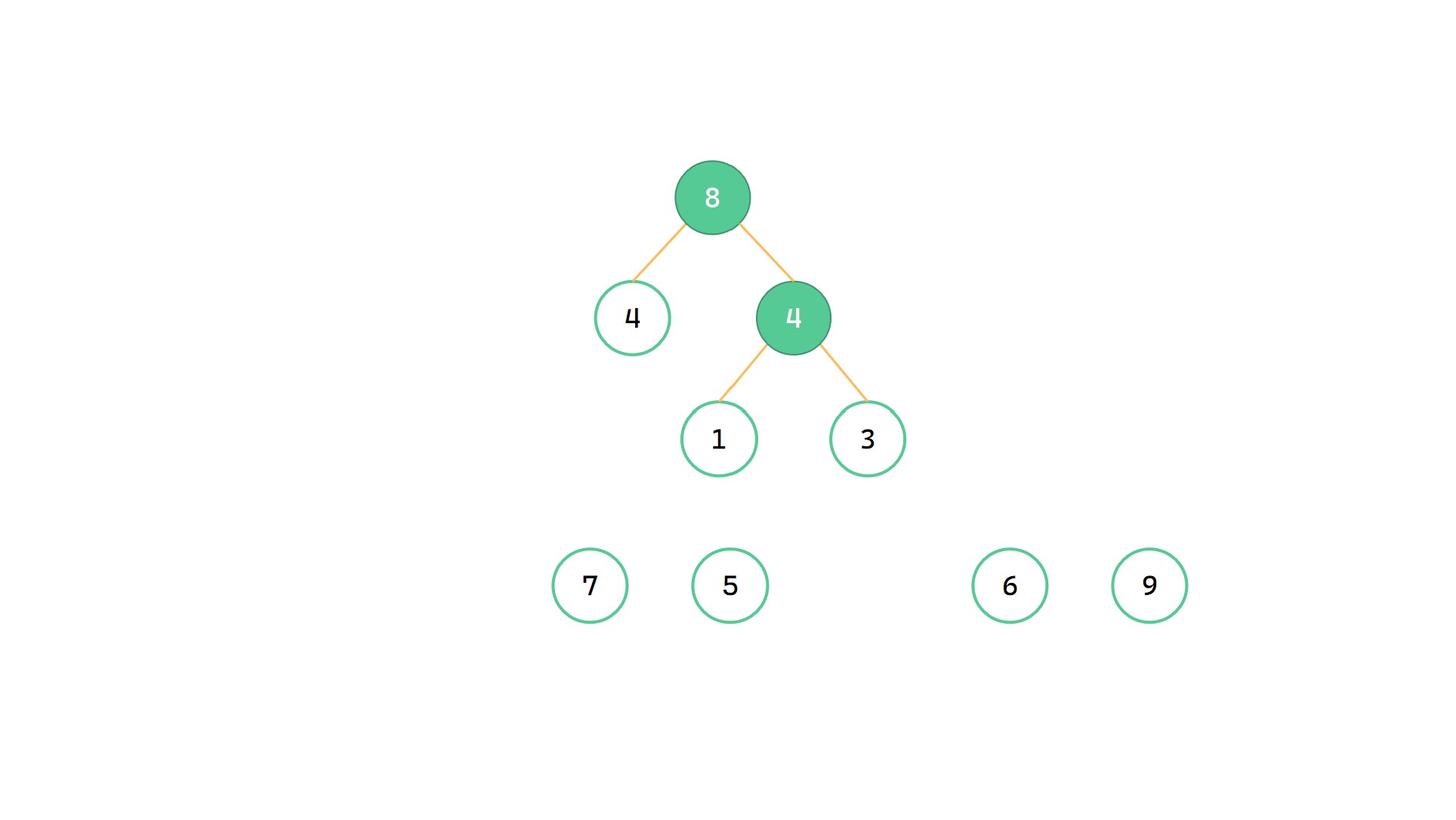
（4）

最小的 5 和 6 合并为 11

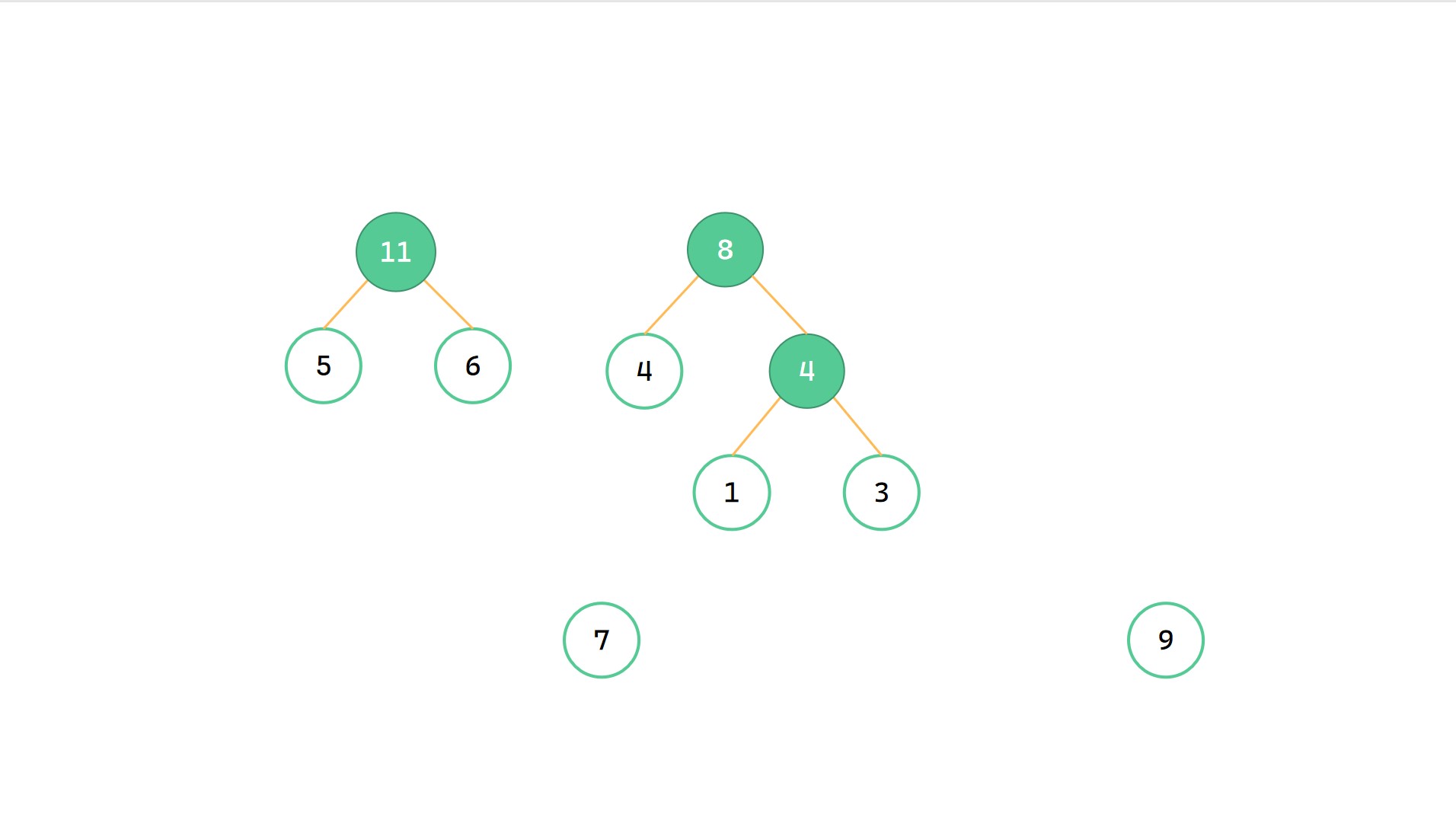
（5）

最小的 7 和 8 合并为 15

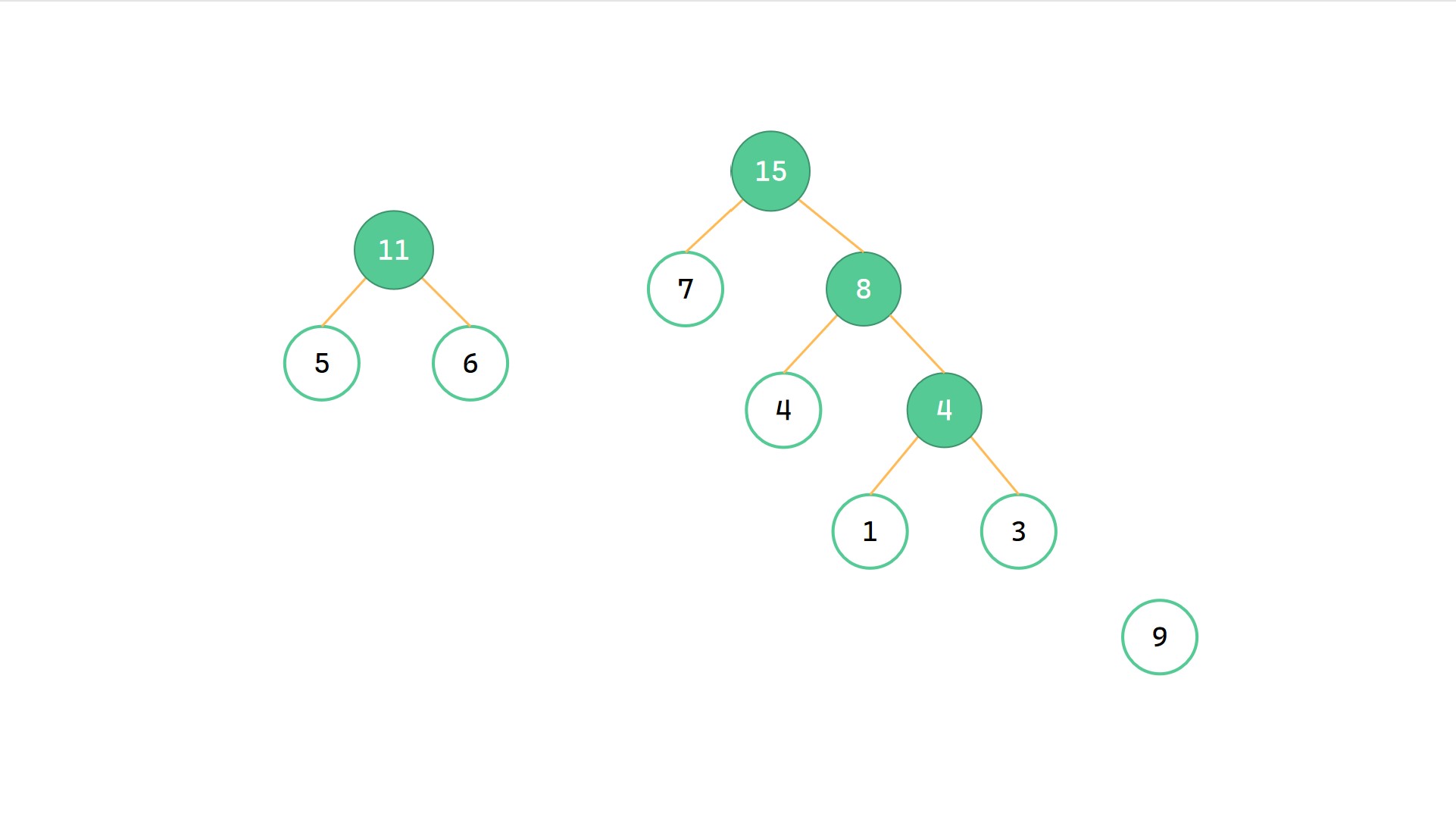
（6）

最小的 9 和 11 合并为 20

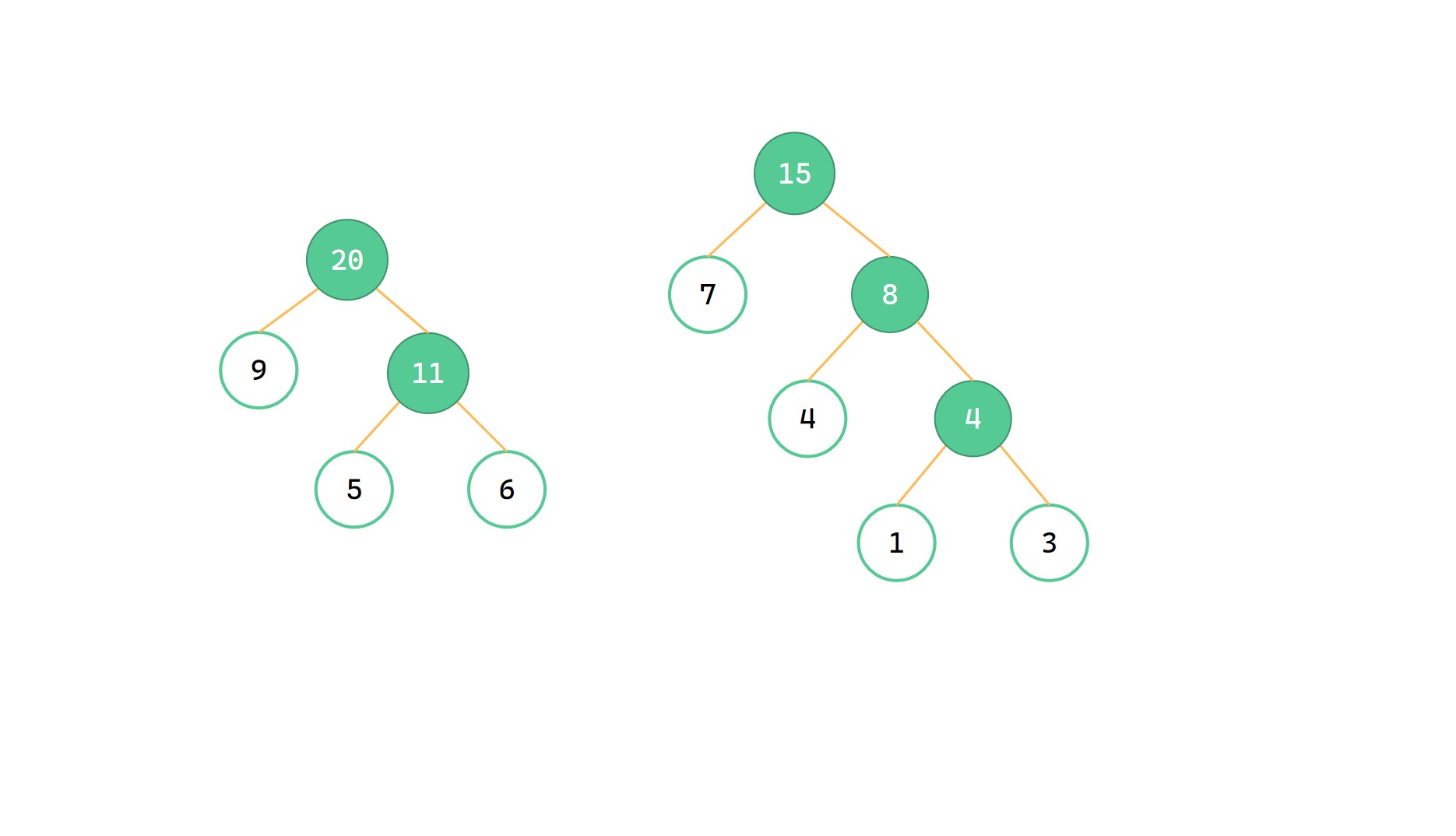
（7）

最小的 15 和 20 合并为 35

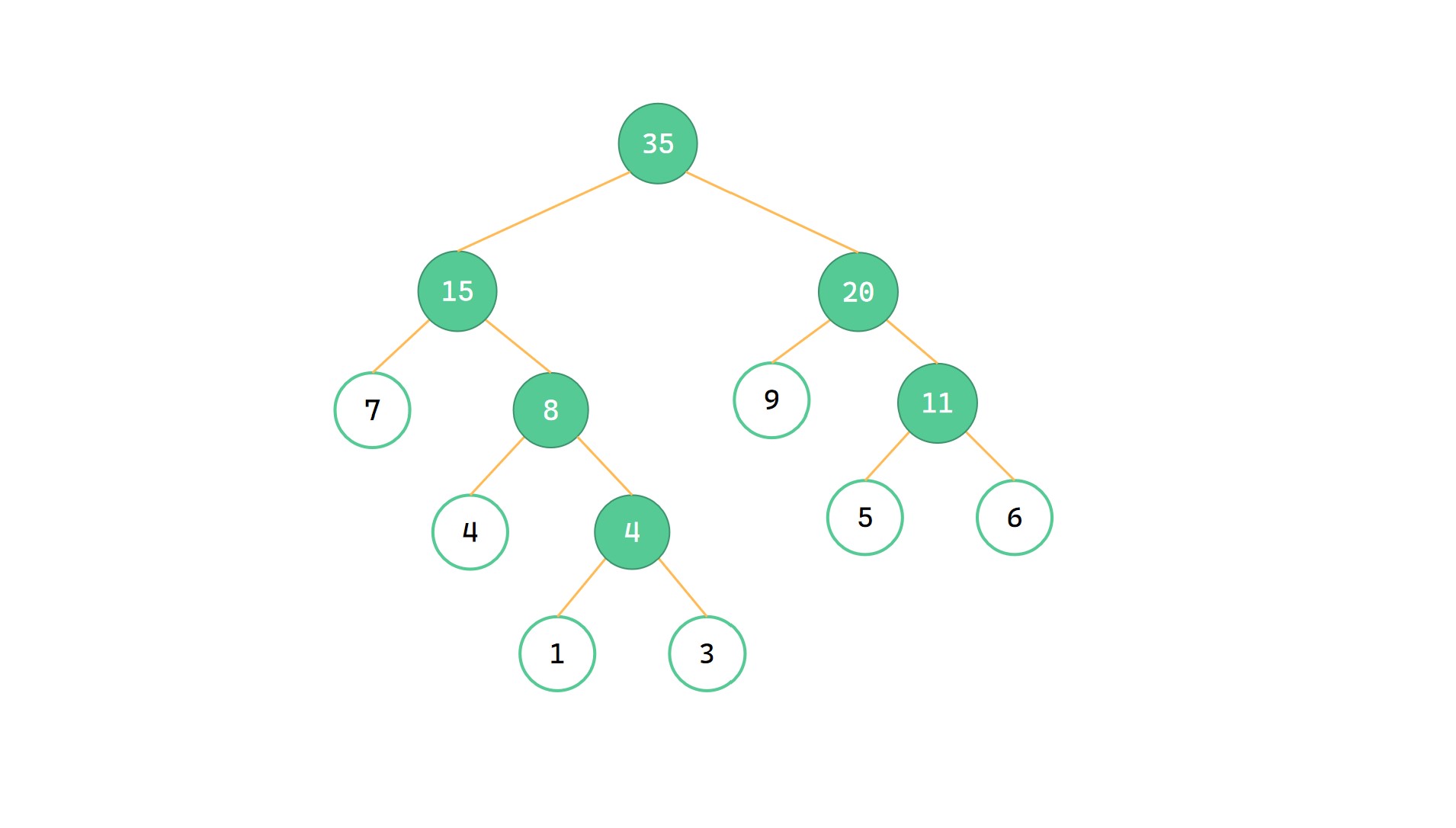
（8）

计算 WPL

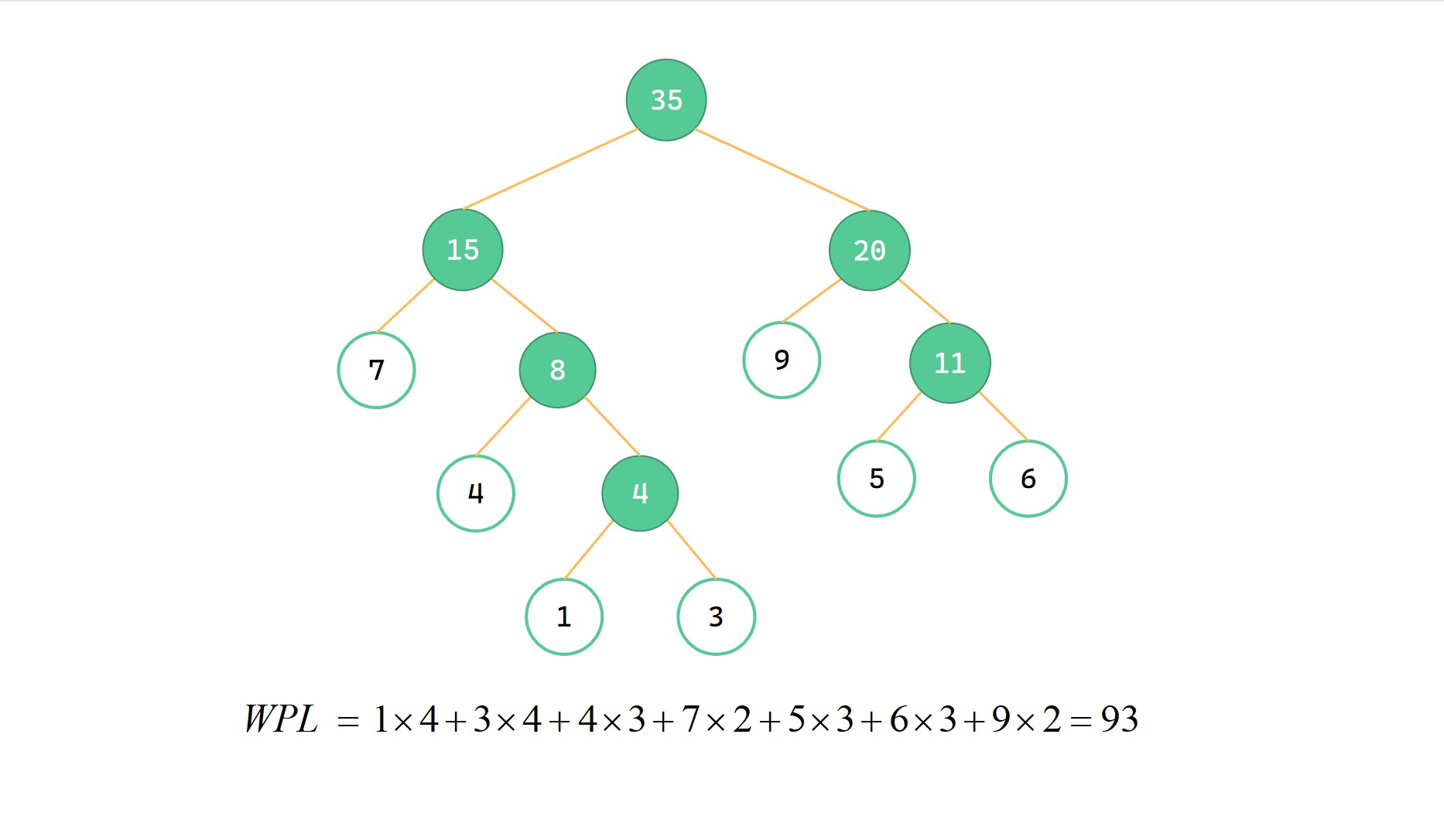
哈夫曼树相关试题

哈夫曼树

Acwing 3531.哈夫曼树

#include<iostream>
#include<queue>
#include<vector>
#include<functional>
using namespace std;

int n, ans = 0;
priority_queue<int, vector<int>, greater<int> > heap;  //小根堆

int main()
    ios::sync_with_stdio(false);
    cin.tie(0);
    
    cin>>n;
    while(n--)
        int x; cin>>x;
        heap.push(x);
    
    
    while(heap.size() > 1)
        int a = heap.top();
        heap.pop();
        int b = heap.top();
        heap.pop();
        
        ans += a + b;
        heap.push(a + b);
    
    cout<<heap.top()<<endl;
    cout<<ans;

一切都是命运石之门的选择，本文章来源于博客园，作者：Amαdeus，出处：https://www.cnblogs.com/MAKISE004/p/17084223.html，未经允许严禁转载