数据结构之哈夫曼树
Posted 迷途纸鸢
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了数据结构之哈夫曼树相关的知识,希望对你有一定的参考价值。
1.哈夫曼树
假设有n个权值{w1, w2, ..., wn},试构造一棵含有n个叶子结点的二叉树,每个叶子节点带权威wi,则其中带权路径长度WPL最小的二叉树叫做最优二叉树或者哈夫曼树。
特点:哈夫曼树中没有度为1的结点,故由n0 = n2+1以及m= n0+n1+n2,n1=0可推出m=2*n0-1,即一棵有n个叶子节点的哈夫曼树共有2n-1个节点。
2.哈夫曼编码
通信传送的目标是使总码长尽可能的短。
变长编码的原则:
1.使用频率高的字符用尽可能短的编码(这样可以减少数据传输量);
2.任一字符的编码都不能作为另一个字符编码的开始部分(这样就使得在两个字符的编码之间不需要添加分隔符号)。这种编码称为前缀编码。
根据每种字符在电文中出现的次数构造哈夫曼树,将哈夫曼树中每个分支结点的左分支标上0,右分支标上1,把从根结点到每个叶子结点的路径上的标号连接起来,作为叶结点所代表的字符的编码。这样得到的编码称为哈夫曼编码。
思考:为什么哈夫曼编码符合变长编码的原则?哈夫曼树所构造出的编码的长度是不是最短的?
哈夫曼树求得编码为最优前缀码的原因: 在构造哈夫曼树的过程中:
1.权值大的在上层,权值小的在下层。满足出现频率高的码长短。
2.树中没有一片叶子是另一叶子的祖先,每片叶子对应的编码就不可能是其它叶子编码的前缀。即上述编码是二进制的前缀码。
假设每种字符在电文中出现的次数为wi (出现频率即为权值),其码长为li,电文中只有n种字符,则编码后电文总码长为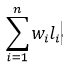
3.哈夫曼编码实例
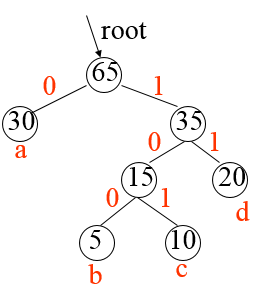
四种字符以及他们的权值:a:30, b:5, c:10, d:20
第一步:构建哈夫曼树
第二步:为哈夫曼树的每一条边编码
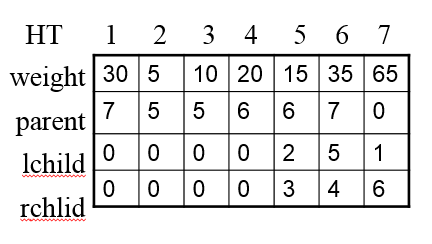
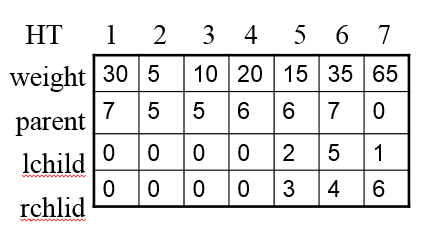
第三步:生成哈夫曼编码表
代码如下:
1 #include "stdafx.h" 2 #include<iostream> 3 #include<string> 4 #include<cstring> 5 #include<iomanip> 6 using namespace std; 7 #define n 4 //叶子数 8 #define m 2 * n - 1 //节点总个数(m) 9 #define MAXSIZE 1000 10 typedef char TElemType; 11 typedef char * HuffmanCode[n+1]; 12 13 typedef struct { 14 unsigned int weight; //节点的权值 15 int parent, lchild, rchild; //双亲、左孩子、右孩子 16 }HTNode,*HuffmanTree; 17 18 typedef char * HuffmanCode[n + 1]; 19 20 void Select(HuffmanTree HT, int k, int &s1, int &s2) ////在HT[1...k]里选择parent为0的且权值最小的2结点,其序号分别为s1,s2,parent不为0说明该结点已经参与构造了,故不许再考虑 21 { 22 unsigned int temp = MAXSIZE, tmpi = 0; 23 for (int i = 1; i <= k; i++) 24 { 25 if (!HT[i].parent) 26 { 27 if (temp > HT[i].weight) 28 { 29 temp = HT[i].weight; 30 tmpi = i; 31 } 32 } 33 } 34 s1 = tmpi; 35 36 temp = MAXSIZE; 37 tmpi = 0; 38 for (int i = 1; i <= k; i++) 39 { 40 if ((!HT[i].parent) && i != s1) 41 { 42 if (temp > HT[i].weight) 43 { 44 temp = HT[i].weight; 45 tmpi = i; 46 } 47 } 48 } 49 s2 = tmpi; 50 } 51 void CreateHuffmanTree(HuffmanTree &HT,int *w) 52 { 53 if (n <= 1) return; 54 HT = new HTNode[m + 1]; //0号单元未用,所以需要动态分配m+1个单元,HT[m]表示根节点 55 for (int i = 1; i <= n; i++) //HT前n个分量存储叶子节点,他们均带有权值 56 { 57 HT[i].weight = w[i]; 58 HT[i].parent = 0; 59 HT[i].lchild = 0; 60 HT[i].rchild = 0; 61 } 62 for (int i=n+1; i <= m; i++) //HT后m-n个分量存储中间结点,最后一个分量显然是整棵树的根节点 63 { 64 HT[i].weight = 0; 65 HT[i].parent = 0; 66 HT[i].lchild = 0; 67 HT[i].rchild = 0; 68 } 69 for (int i = n + 1; i <= m; i++) //开始构建哈夫曼树,即创建HT的后m-n个结点的过程,直至创建出根节点。用哈夫曼算法 70 { 71 int s1, s2; 72 Select(HT, i - 1, s1, s2); //在HT[1...i-1]里选择parent为0的且权值最小的2结点,其序号分别为s1,s2,parent不为0说明该结点已经参与构造了,故不许再考虑 73 HT[s1].parent = i; 74 HT[s2].parent = i; 75 HT[i].lchild = s1; 76 HT[i].rchild = s2; 77 HT[i].weight = HT[s1].weight + HT[s2].weight; 78 } 79 } 80 81 82 83 void coutHuffmanTree(HuffmanTree HT, char ch[]) //打印哈弗曼树 84 { 85 cout << endl; 86 cout << "Data Weight Parent Lchild rchild" << endl; 87 for (int i = 1; i <= m; i++) 88 { 89 if (i > n) 90 { 91 cout << left << setw(5)<< "-"<< left << setw(7) << HT[i].weight <<left << setw(7) << HT[i].parent << left << setw(7) //<<left<<setw()需要头文件#include<iomanip>支持 92 << HT[i].lchild << left << setw(5) << HT[i].rchild << endl; 93 } 94 else 95 { 96 cout << left << setw(5)<< ch[i] << left << setw(7) << HT[i].weight << left << setw(7) << HT[i].parent << left << setw(7) 97 << HT[i].lchild << left << setw(5) << HT[i].rchild << endl; 98 } 99 } 100 } 101 102 void CreatHuffmanCode(HuffmanTree HT, HuffmanCode &HC) //哈弗曼编码 103 { 104 char temp[n]; 105 temp[n - 1] = ‘\0‘; //编码的结束符 106 int start,c,f; 107 for (int i = 1; i <= n; i++) //对于第i个待编码字符即第i个带权值的叶子节点 108 { 109 start = n - 1; //编码生成以后,start将指向编码的起始位置 110 c = i; 111 f = HT[i].parent; 112 while (f != 0) //f不是根节点的父节点 113 { 114 if (HT[f].lchild == c) 115 { 116 temp[--start] = ‘0‘; 117 } //注意:由于哈夫曼树中只存在叶子节点和度为2的节点,所以除开叶子节点,节点一定有左右2个分支 118 else 119 { 120 temp[--start] = ‘1‘; 121 } 122 c = f; 123 f = HT[f].parent; 124 } 125 HC[i] = new char[n - start]; //每次tmp的后n-start个位置有编码存在 126 strcpy(HC[i], &temp[start]); //将tmp的后n-start个元素分给H[i]指向的的字符串 127 } 128 } 129 130 void coutHuffmanCoding(HuffmanCode HC, char ch[]) //打印哈夫曼编码表 131 { 132 cout << endl; 133 for (int i = 1; i <= n; i++) 134 cout << ch[i] << ":"<< HC[i] << endl; 135 cout << endl; 136 } 137 138 void decodingHuffmanCode(HuffmanTree HT, char *ch, char testDecodingStr[], int len, char *result) //解码(有能力的话就看一下,这个函数不是数据结构考察范围) 139 { 140 int p = m; //HT的最后一个节点是根节点,前n个节点是叶子节点 141 int i = 0; //指示测试串中的第i个字符 142 int j = 0; //指示结果串中的第j个字符 143 while (i < len) 144 { 145 if (testDecodingStr[i] == ‘0‘) 146 { 147 p = HT[p].lchild; 148 } 149 if (testDecodingStr[i] == ‘1‘) 150 { 151 p = HT[p].rchild; 152 } 153 if (p <= n) //p<=N则表明p为叶子节点,因为在构造哈夫曼树HT时,HT的m个节点中前n个节点为叶子节点 154 { 155 result[j] = ch[p]; 156 j++; 157 p = m; //p重新指向根节点 158 } 159 i++; 160 } 161 result[j] = ‘\0‘; //结果串的结束符 162 } 163 164 int main() 165 { 166 HuffmanTree HT; 167 TElemType ch[n + 1]; 168 int w[n + 1]; 169 cout << "请输入" <<n<<"个字符以及该字符对应的权值(如:a,20):"<< endl; 170 for (int i = 1; i <= n; i++) 171 { 172 cin >> ch[i] >> w[i]; 173 getchar(); 174 } 175 CreateHuffmanTree(HT,w); 176 coutHuffmanTree(HT, ch); 177 178 HuffmanCode HC; //HC有n个元素,每个元素是一个指向字符串的指针,即每个元素是一个char * 的变量 179 CreatHuffmanCode(HT, HC); 180 coutHuffmanCoding(HC, ch); 181 182 char testDecodingStr[] = "01000101101110";//解码测试用例:abaccda----01000101101110 ,也可以自己改 183 int testDecodingStrlen = 14; 184 cout << "编码" << testDecodingStr << "对应的字符串是:"; 185 char result[30]; //存储解码以后的字符串 186 decodingHuffmanCode(HT, ch, testDecodingStr, testDecodingStrlen, result);////解码(译码),通过一段给定的编码翻译成对应的字符串 187 cout << result << endl; 188 return 0; 189 }
常见问题解决: 转载于:https://blog.csdn.net/y609532842/article/details/49705973
strcpy函数的话visual studio 2017 会报错:
error C4996: ‘strcpy‘: This function or variable may be unsafe. Consider using strcpy_s instead.
那么:
出现这个错误时,是因为strcpy函数不安全造成的溢出。
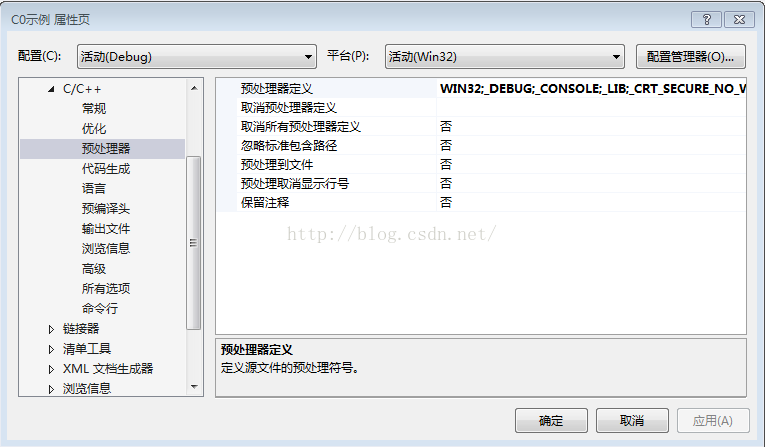
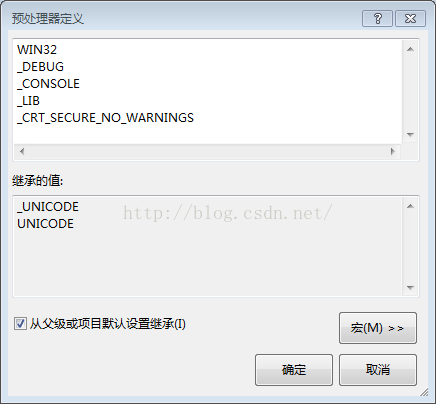
解决方法是:找到【项目属性】,点击【C++】里的【预处理器】,对【预处理器】进行编辑,在里面加入一段代码:_CRT_SECURE_NO_WARNINGS。
图示:
或者:点击 [调试] 最后一项 :ConsaleApplication 属性 也会出现上述界面,记下来步骤就一样了
以上是关于数据结构之哈夫曼树的主要内容,如果未能解决你的问题,请参考以下文章