统计学离散型变量和连续型变量有啥区别？

Posted 2023-03-15

统计学离散型变量和连续型变量有什么区别？在何种情况下可以编制单项式变量数列？在何种情况下可以编制组距式变量数列？

两者的区别：

1、变量按其数值表现是否连续。

连续变量是一直叠加上去的，增长量可以划分为固定的单位，即：1,2,3…… 例如：一个人的身高，他首先长到1.51，然后才能长到1.52，1.53……。

而离散变量则是通过计数方式取得的，即是对所要统计的对象进行计数，增长量非固定的，如：一个地区的企业数目可以是今年只有一家，而第二年开了十家；一个企业的职工人数今年只有10人，第二年一次招聘了20人等。 

2、变量值的变动幅度不同。

对离散变量，如果变量值的变动幅度小，就可以一个变量值对应一组，称单项式分组。如居民家庭按儿童数或人口数分组，均可采用单项式分组。

离散变量如果变量值的变动幅度很大，变量值的个数很多，则把整个变量值依次划分为几个区间，各个变量值则按其大小确定所归并的区间，区间的距离称为组距，这样的分组称为组距式分组。

也就是说，离散变量根据情况既可用单项式分组，也可用组距式分组。在组距式分组中，相邻组既可以有确定的上下限，也可将相邻组的组限重叠。

扩展资料：

1、离散变量是指其数值只能用自然数或整数单位计算的则为离散变量。例如，企业个数、职工人数、设备台数等，只能按计量单位数计数，这种变量的数值一般用计数方法取得。

2、而连续变量是在一定区间内可以任意取值的变量，其数值是连续不断的，相邻两个数值可作无限分割，即可取无限个数值。例如，生产零件的规格尺寸、人体测量的身高、体重、胸围等为连续变量，其数值只能用测量或计量的方法取得。

3、离散变量的概率分布，常用的有二项分布、泊松(Poisson)分布。其余的还有两点分布、几何分布、超几何分布等概率分布。

参考资料：百度百科-连续变量、百度百科-离散变量

参考技术A

1 离散变量是指其数值只能用自然数或整数单位计算的则为离散变量.例如,企业个数,职工人数,设备台数等,只能按计量单位数计数,这种变量的数值一般用计数方法取得.

2 反之,在一定区间内可以任意取值的变量叫连续变量,其数值是连续不断的,相邻两个数值可作无限分割,即可取无限个数值.例如,生产零件的规格尺寸,人体测量的身高,体重,胸围等为连续变量,其数值只能用测量或计量的方法取得.

3 如果变量可以在某个区间内取任一实数，即变量的取值可以是连续的，这随机变量就称为连续型随机变量，比如，公共汽车每15分钟一班，某人在站台等车时间x是个随机变量，x的取值范围是[0,15)，它是一个区间，从理论上说在这个区间内可取任一实数3.5、√20等，因而称这随机变量是连续型随机变量。

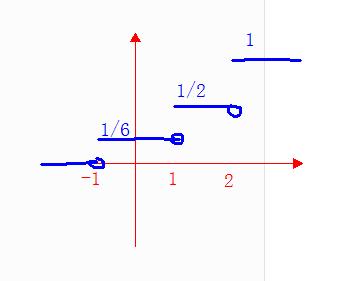
扩展资料：

变量按其数值表现是否连续，分为连续变量和离散变量。离散变量指变量值可以按一定顺序一一列举，通常以整数位取值的变量。如职工人数、工厂数、机器台数等。有些性质上属于连续变量的现象也按整数取值，即可以把它们当做离散变量来看待。例如年龄、评定成绩等虽属连续变量，但一般按整数计算，按离散变量来处理。离散变量的数值用计数的方法取得。

离散变量的概率分布，常用的有二项分布、泊松(Poisson)分布。其余的还有两点分布、几何分布、超几何分布等概率分布。

连续型随机变量是指如果随机变量X的所有可能取值不可以逐个列举出来，而是取数轴上某一区间内的任一点的随机变量。例如，一批电子元件的寿命、实际中常遇到的测量误差等都是连续型随机变量。

对于随机变量X，若存在一个非负的可积函数f(x)，使得对任意实数x，则称X为连续性随机变量。其中f(x)为X的概率分布密度函数，简称概率密度记为X～f(x)。

相关性质：

由定义可知，

若f（x）在点x连续，则有F’（x）=f（x）

f（x）是可积，则它的原函数F（x）连续；

3.对于任意两个实数x1，x2（假设x1<x2），都有：

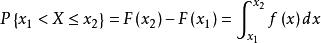
X取任一指定实数值a的概率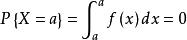，  ,这样在计算连续性随机变量落在某一区间的概率时，可以不必区分该区间是开区间还是闭区间。

有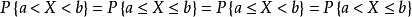 

尽管PX=a=0，但X=a并不是不可能事件。同样，一个事件的概率为1，并不意味这个事件一定是必然事件。

当提到一个随机变量X的概率分布，指的是它的分布函数，当X是连续型时指的是它的概率密度，当X是离散型时指的是它的分布律。

变量按其数值表现是否连续，分为连续变量和离散变量。连续变量的数值是连接不断的，相邻两值之间可作无限分割，例如，身高、体重、年龄等都是连续变量。

简单随机取样就是重复进行同一随机试验，也就是指每次试验都在同一组条件下进行，因而每次试验得到什么结果，其可能程度都是固定不变的。对于有限总体，简单随机抽样意味着每次抽出一个元素后，放还再抽，若不放还，总体的成分将有所改变，那么再抽时，出现各种结果的可能程度就相对地改变了。至于无限总体则没有区分“放回”或“不放回”的必要。

参考资料：百度百科-连续型变量  百度百科-离散变量

参考技术B

一、获取方式不同

离散型变量：离散型变量则是通过计数方式取得的，即是对所要统计的对象进行计数，增长量非固定的。

连续型变量：连续型变量是一直叠加上去的，增长量可以划分为固定的单位。

二、域不同

离散型变量：离散型变量的域(即对象的集合S)是离散的。

连续型变量：连续型变量的域(即对象的集合S)是连续的。

二、分组方式不同

离散型变量：如果变量值的变动幅度小，就可以一个变量值对应一组，称单项式分组。如果变量值的变动幅度很大，变量值的个数很多，则把整个变量值依次划分为几个区间，各个变量值则按其大小确定所归并的区间，区间的距离称为组距，这样的分组称为组距式分组。

连续型变量：连续型变量由于不能一一列举其变量值，只能采用组距式的分组方式，且相邻的组限必须重叠。

扩展资料

离散变量的概率分布

1、二项分布

2、泊松分布

3、二点分布

3、几何分布

4、超几何分布

参考资料来源：百度百科-离散变量

百度百科-连续变量

参考技术C 离散变量是指其数值只能用自然数或整数单位计算的则为离散变量.例如,企业个数,职工人数,设备台数等,只能按计量单位数计数,这种变量的数值一般用计数方法取得.

反之,在一定区间内可以任意取值的变量叫连续变量,其数值是连续不断的,相邻两个数值可作无限分割,即可取无限个数值.例如,生产零件的规格尺寸,人体测量的身高,体重,胸围等为连续变量,其数值只能用测量或计量的方法取得.

如果变量可以在某个区间内取任一实数，即变量的取值可以是连续的，这随机变量就称为连续型随机变量，
比如，公共汽车每15分钟一班，某人在站台等车时间x是个随机变量，
x的取值范围是[0,15)，它是一个区间，从理论上说在这个区间内可取任一实数3.5、√20等，因而称这随机变量是连续型随机变量。本回答被提问者采纳 参考技术D 接楼上的。
采取单项式变量数列和组距式数列分组，主要取决于变量的类型和变量的变动幅度。
对于连续型变量，一般只能编制组距式变量数列；
对于离散型变量，如果变量值个数较多，并且变动幅度较大时，应该编制组距式变量数列， 对于变量值较少的离散型数据，一般编制单项式变量数列。（变量值的多少，跟数据量的多少是不一样的，有时候数据量很多，但是变量值却很少。比如研究一个班（110人）的年龄结构，有110个数据，但是有可能只有两三个变量值，假设最小的20岁，最大的22岁，那么就只有三个变量值，那么分组时就按照单项式变量数列分组）