什么是曲面及曲面在画法几何中起到什么作用？

Posted 2023-04-19

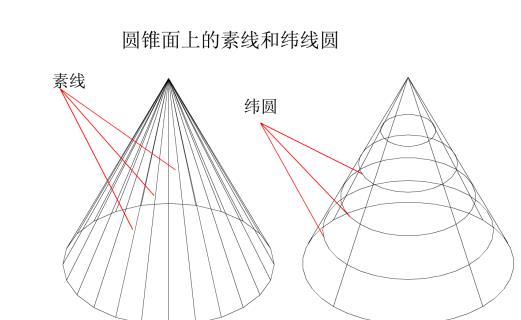
参考技术A

曲面可以看作是一动线在空间运动的轨迹,该动线称为母线，母线处于曲面上任一位置时，称为素线。

一个几何体在美术方法的表现中采用的轮廓内的表现方法，例如几何体内的光线明暗的表现方法所用 的素描线。

扩展资料：                           

由于画法几何所研究的是空间形体与它在平面上的图形之间的关系，因而在培养和发展学生对三维形状和相关位置的空间逻辑思维和形象思维能力方面起着极其重要的作用。

在这里，图形是直接用来研究空间形体的几何形状和解决空间几何问题的工具，因此，对画法几何在平面上的图形有一系列的要求。主要有：

1、图形应当具有可逆性，也就是说，根据图形能够准确地恢复所画形体的形状和大小；

2、图形在满足其功能的前提下具有一定的直观性，以便根据图形能比较容易地想象出所画的形体的形状和大小；

3、绘制图形应较为简便；

4、图形以及由之进行的作图应足够准确。

微积分——曲面积分

曲面积分

文章目录

• 曲面积分
• • 一.第一型曲面积分
  • • 1.性质
    • 2.几何意义
    • 3.计算
  • 二.第二型曲面积分
  • • 1.有向曲面及有向曲面的投影
    • 2.与第一型曲面积分的联系
    • 3.性质
    • • ①可加性
      • ②有向性
      • ③线性性质
      • ④
    • 4.计算
    • • ①分面计算法
      • • （1）计算$\underset{\Sigma }{\iint }Rdxdy=\underset{\Sigma }{\iint }R\cos \gamma dS$
        • （2）计算$\underset{\Sigma }{\iint }Pdydz=\underset{\Sigma }{\iint }P\cos \alpha dS$
        • （3）计算$\underset{\Sigma }{\iint }Qdxdz=\underset{\Sigma }{\iint }Q\cos \beta dS$
      • ②统一到一个坐标面计算
  • 三.高斯公式
  • • 1.高斯公式
    • • （表达了空间有界区域上的三重积分与其边界曲面上的曲面积分之间的关系）
    • 2.通量
    • • 定义：
    • 3.散度
    • • 定义
  • 四.斯托克斯公式
  • • 1.斯托克斯公式
    • • 注
    • 2.空间第二型曲线积分与路径无关性质
    • 3.环流量与旋度

一.第一型曲面积分

对面积的曲面积分

1.性质

​ 完全类似于第一型曲线积分

2.几何意义

​ 被积函数$f(x,y,z)=1,$曲面面积为${\iint }_{\Sigma }dS$

3.计算

​ 化为二重积分

​ 设有光滑曲面
$$\Sigma :z=z(x,y),(x,y)\in D_{xy}$$
$f(x,y,z)$在$\Sigma$上连续，则曲面积分${\iint }_{\Sigma }f(x,y,z)dS$存在，且有
$${\iint }_{\Sigma }f(x,y,z)dS={\iint }_{\Sigma }f(x,y,z(x,y))\sqrt{1+z_x^{\prime 2}(x,y)+z_y^{\prime 2}(x,y)}dxdy$$

其中，$dxdy$是$dS$在$xOy$平面上的投影

若曲面方程为

​ $x=x(y,z),(y,z)\in D_{yz}$或$y=y(x,z),(x,z)\in D_{xz}$,方法类似

二.第二型曲面积分

在坐标面投影的曲面积分

1.有向曲面及有向曲面的投影

曲面可分为双侧曲面、单侧曲面

选定了侧的曲面叫有向曲面，其方向用法向量的指向表示

设$\Sigma$为有向平面，其面积为$\Delta S$，$\Sigma$在$xOy$面上的投影记为$(\Delta S{)}_{xy},\Sigma$在$xOy$面上的投影面积为$(\Delta \sigma {)}_{xy}⩾0,$则规定$(\Delta S{)}_{xy}=\Delta S\cos \gamma$

​ $(\Delta \sigma {)}_{xy}=\Delta S|\cos \gamma |$

即
$$(\Delta S{)}_{xy}=\{\begin{array}{lr}(\Delta \sigma {)}_{xy}& 当\cos \gamma >0\\ -(\Delta \sigma {)}_{xy}& 当\cos \gamma <0\\ 0& 当\cos \gamma =0\end{array}$$
类似可规定$(\Delta S{)}_{xz},(\Delta S{)}_{yz}$

设$\Sigma$为有向曲面，其面积为$\Delta S$，$\Sigma$在$xOy$面上的投影记为$Tessellation\; (曲面细分)\; Displacement\; Mapping\; (贴图置换)$

微分几何主要研究啥

代数53 ----常见二次曲面

微积分——曲面积分

渲染管道几何阶段三“曲面细分着色器”

渲染管道几何阶段三“曲面细分着色器”