代数53 ----常见二次曲面
Posted 炫云云
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了代数53 ----常见二次曲面相关的知识,希望对你有一定的参考价值。
文章目录
二次曲面
曲面的一般方程 S : F ( x , y , z ) = 0 S: F(x, y, z)=0 S:F(x,y,z)=0.
若曲面方程 F ( x , y , z ) = 0 F(x, y, z)=0 F(x,y,z)=0 的左端是关于 x , y , z x, y, z x,y,z 的多项式, 则称这个多项式的次数为曲面的次数.
三元二次方程
a
1
x
2
+
a
2
y
2
+
a
3
z
2
+
b
1
x
y
+
b
2
y
z
+
b
3
z
x
+
c
1
x
+
c
2
y
+
c
3
z
+
d
=
0
a_{1} x^{2}+a_{2} y^{2}+a_{3} z^{2}+b_{1} x y+b_{2} y z+b_{3} z x+c_{1} x+c_{2} y+c_{3} z+d=0
a1x2+a2y2+a3z2+b1xy+b2yz+b3zx+c1x+c2y+c3z+d=0
所确定的曲面称为二次曲面, 其中二次项系数不全为 0 .
一些常见的旋转曲面
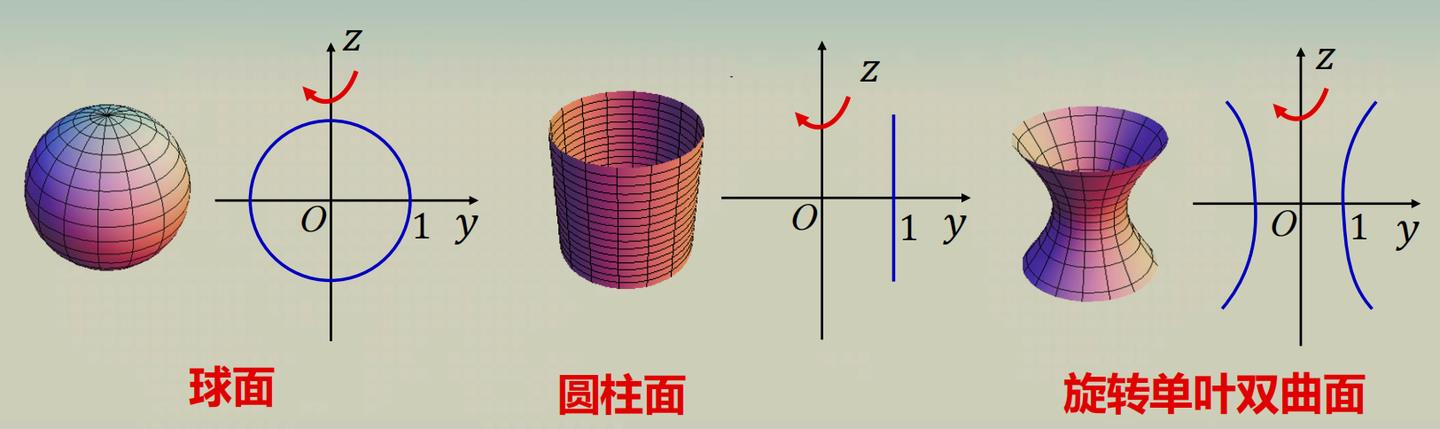
球
面
:
S
1
:
x
2
+
y
2
+
z
2
=
1.
圆
柱
面
:
S
2
:
x
2
+
y
2
=
1.
旋
转
单
叶
双
曲
面
:
S
3
:
x
2
+
y
2
−
z
2
=
1
球面:S_{1}: x^{2}+y^{2}+z^{2}=1 . \\quad \\\\ 圆柱面:S_{2}: x^{2}+y^{2}=1 . \\quad \\\\ 旋转单叶双曲面:S_{3}: x^{2}+y^{2}-z^{2}=1\\quad
球面:S1:x2+y2+z2=1.圆柱面:S2:x2+y2=1.旋转单叶双曲面:S3:x2+y2−z2=1
圆环面不是二次曲面
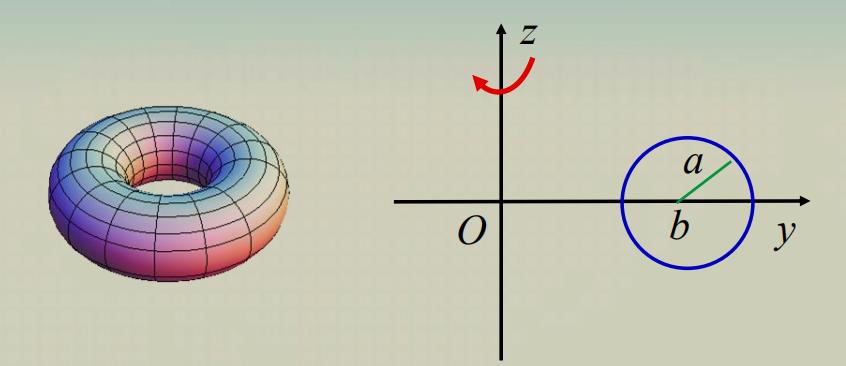
C
:
{
(
y
−
b
)
2
+
z
2
=
a
2
x
=
0
(
b
>
a
>
0
)
\\begin{array}{c} C:\\left\\{\\begin{array}{c} (y-b)^{2}+z^{2}=a^{2} \\\\ x=0 \\end{array}\\right. \\\\ (b>a>0) \\end{array}
C:{(y−b)2+z2=a2x=0(b>a>0)
S : ( x 2 + y 2 + z 2 + b 2 − a 2 ) 2 = 4 b 2 ( x 2 + y 2 ) S:\\left(x^{2}+y^{2}+z^{2}+b^{2}-a^{2}\\right)^{2}=4 b^{2}\\left(x^{2}+y^{2}\\right) S:(x2+y2+z2+b2−a2)2=4b2(x2+y2)
二次曲面基本类型
椭球面、双曲面、抛物面、二次锥面和二次柱面
关于曲面的两项研究任务:
一、根据曲面的几何特征,建立曲面的一般方程和参数方程;
二、根据曲面方程,讨论曲面的几何性质,描绘曲面的图形 .
椭球面
定
义
1
\\large\\color{magenta}{\\boxed{\\color{brown}{定义1} }}
定义1 方程
S
:
x
2
a
2
+
y
2
b
2
+
z
2
c
2
=
1
S: \\frac{x^{2}}{a^{2}}+\\frac{y^{2}}{b^{2}}+\\frac{z^{2}}{c^{2}}=1
S:a2x2+b2y2+c2z2=1 所表示的曲面称为中心在原点的椭球面
.
.
.
其中
a
,
b
,
c
a, b, c
a,b,c 为正的常数, 称为粗球面的半轴.
注 1 : \\Large\\color{violet}{注1:} 注1:当 a = b = c a=b=c a=b=c 时, 表示球面, S : x 2 + y 2 + z 2 = a 2 S: x^{2}+y^{2}+z^{2}=a^{2} S:x2+y2+z2=a2
注 2 : \\Large\\color{violet}{注2:} 注2:当 a = b a=b a=b 时,表示旋转椭圆面 .
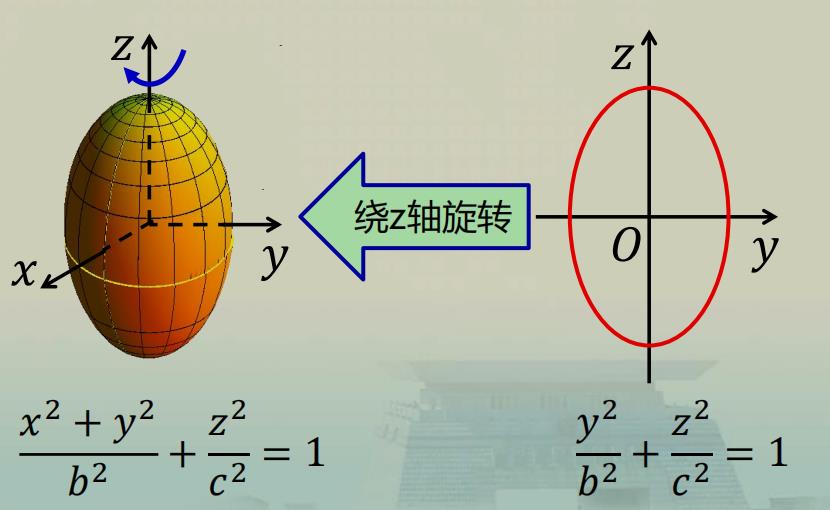
椭球面想象为单位球面的伸缩