微分几何主要研究啥
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了微分几何主要研究啥相关的知识,希望对你有一定的参考价值。
参考技术A 微分几何是运用微积分的理论研究空间的几何性质的数学分支学科.古典微分几何研究三维空间中的曲线和曲面,而现代微分几何开始研究更一般的空间----流形.微分几何与拓扑学等其他数学分支有紧密的联系,对物理学的发展也有重要影响.爱因斯坦的广义相对论就以微分几何中的黎曼几何作为其重要的数学基础.微分几何学以光滑曲线(曲面)作为研究对象,所以整个微分几何学是由曲线的弧线长、曲线上一点的切线等概念展开的.既然微分几何是研究一般曲线和一般曲面的有关性质,则平面曲线在一点的曲率和空间的曲线在一点的曲率等,就是微分几何中重要的讨论内容,而要计算曲线或曲面上每一点的曲率就要用到微分的方法.
在曲面上有两条重要概念,就是曲面上的距离和角.比如,在曲面上由一点到另一点的路径是无数的,但这两点间最短的路径只有一条,叫做从一点到另一点的测地线.在微分几何里,要讨论怎样判定曲面上一条曲线是这个曲面的一条测地线,还要讨论测地线的性质等.另外,讨论曲面在每一点的曲率也是微分几何的重要内容.
微分几何
在微分几何中,为了讨论任意曲线上每一点邻域的性质,常常用所谓“活动标形的方法”.对任意曲线的“小范围”性质的研究,还可以用拓扑变换把这条曲线“转化”成初等曲线进行研究.
在微分几何中,由于运用数学分析的理论,就可以在无限小的范围内略去高阶无穷小,一些复杂的依赖关系可以变成线性的,不均匀的过程也可以变成均匀的,这些都是微分几何特有的研究方法
近代由于对高维空间的微分几何和对曲线、曲面整体性质的研究,使微分几何和拓扑学、变分学、李群理论等有了密切的关系,这些数学领域和微分几何互相渗透,已成为现代数学的中心课题之一.[2]
微分几何在力学和一些工程技术问题方面有广泛的应用,比如,在弹性薄壳结构方面,在机械的齿轮啮合理论应用方面,都充分应用了微分几何学的理论.
微分几何学的研究对数学其他分支以及力学、物理学、工程学等的影响是不可估量的.如:伪球面上的几何与非欧几何有密切关系;测地线和力学、变分学、拓扑学等有着深刻的联系,是内容丰富的研究课题.这方面有以J.阿达马、H.庞加莱等人为首的优异研究.极小曲面是和复变函数论、变分学、拓扑学关系极为深刻的研究领域,K.魏尔斯特拉斯、J.道格拉斯等人作出过卓越贡献.
微分几何学的研究工具大部分是微积分学.力学、物理学、天文学以及技术和工业的日益增长的要求则是微分几何学发展的重要因素.尽管微分几何学主要研究三维欧几里得空间中的曲线、曲面的局部性质,但它形成了现代微分几何学的基础则是毋庸置疑的.因为依赖于图形的直观性及由它进行类推的方法,即使在今天也未失其重要性.
高等数学:微分积分物理以及几何意义
目录
0、前言
图像处理中会运用到各种算子,要想搞懂每种算子的使用,首先得有微分积分的基础知识。
1、微分
1.1、一元微分
1.1.1、微分的来由
微分<------------------>近似值<---------------->直线增量去近似代替曲线增量的那个直线增量部分---->记号dy------->y的微分---------->dy=Adx

1.1.2、微分的定义

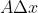 是直线的增量去代替曲线的增量,那么问题来了,A到底是什么东西?
是直线的增量去代替曲线的增量,那么问题来了,A到底是什么东西?
由前边由来可知,A应该是直线的导数,这个直线导数是曲线在该点切线的斜率,因此A应当是导数。
由此推导出来的定理:
 在
在 处可微的充分必要条件是
处可微的充分必要条件是 在
在 处可导。
处可导。
可微必可导的证明:

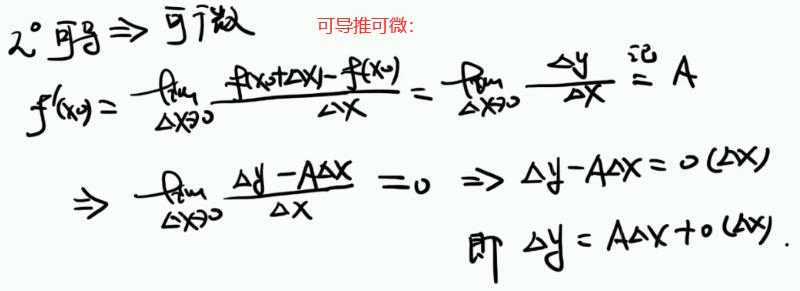
所以一元函数可导和可微是等价的,但是两者的概念不一样。(可导的概念是变化率,而且是个瞬时变化率;而可微的概念是一个近似代替的问题,能不能用直线增量去近似代替曲线增量的问题)(即可导是一个瞬时变化率的问题,可微是一个近似值,但是他们两个在一元函数里边是相互等价的)
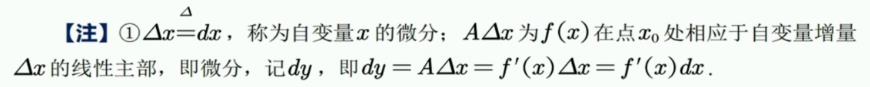
将上式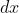 左移,
左移,
导数和微分的几何意义:


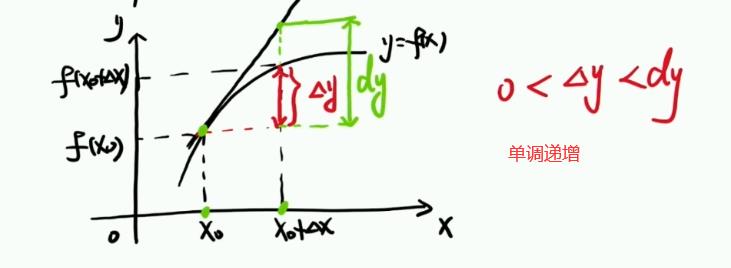
1.2、多元微分
一元与多元的区分就是由原来的一个自变量,变成了多个自变量。
1.2.1、邻域
邻域概念:第二个趋近于邻域是把中间点p给扣掉(大于0就保证取不到中间点p)。

二元函数的几何意义:其实就是形成了一个二维曲面。

1.2.2、重极限


1.2.3、连续


1.2.4、偏导数
一元函数导数:

多元函数偏导数:
对x偏导数:(对x求偏导,把y看成始终不变的 )
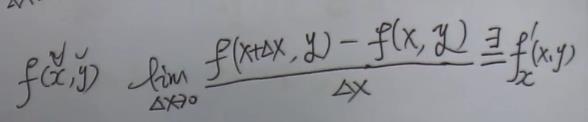
对y的偏导数:
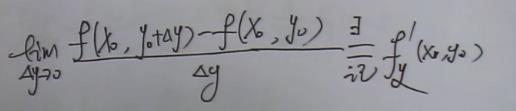

偏导数的几何意义:

高阶偏导数:


 连续指的是混合偏导数连续。
连续指的是混合偏导数连续。
1.2.5、全微分


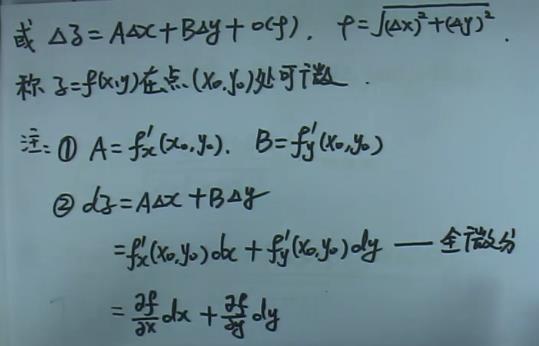
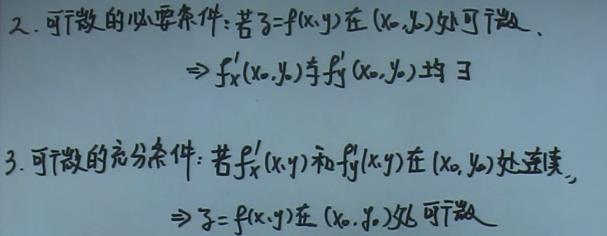
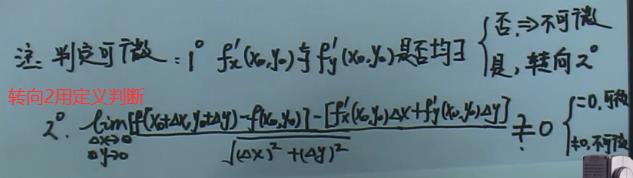

2、积分
2.1、定积分
2.1.1、几何背景
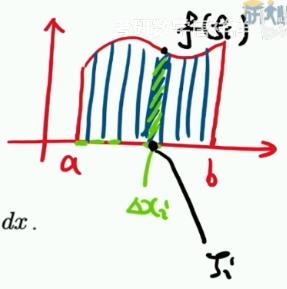
几何背景:就是曲边梯形的面积。曲边梯形的面积(任意划分,看成小矩形的面积)
Q:如何求一个函数 与x=a,x=b与x轴所围成的曲边梯形的面积?
与x=a,x=b与x轴所围成的曲边梯形的面积?
A:首先对曲边梯形任意的划分,然后找一个作为代表,把它近似看作一个小矩形,找其宽度 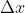 ,并取一点,找到该点的函数值, 对划分的任意多个小矩形都找一点以及该点对应值,相乘(相当于长和宽)并求和,求和就相当于n个矩形的面积加起来。
,并取一点,找到该点的函数值, 对划分的任意多个小矩形都找一点以及该点对应值,相乘(相当于长和宽)并求和,求和就相当于n个矩形的面积加起来。
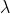 趋近于0,每一个区间都有直径,
趋近于0,每一个区间都有直径,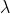 表示n个小区间里边直径的最大值,直径的最大值都趋近于0,保证了你划分的精细程度。
表示n个小区间里边直径的最大值,直径的最大值都趋近于0,保证了你划分的精细程度。
定积分的概念:
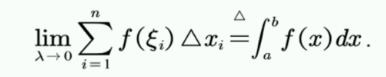
 划分、取 点、求和、取极限。
划分、取 点、求和、取极限。
将上述极限值定义为 一元函数y=f(x)在闭区间a到b上的一个定积分(如果 极限存在,并把该极限定义为f(x)在这个区间上的定积分)。
定积分的几何意义:n项和的极限。

2.2.2、可积性(充分必要条件)
PS:可积一般指定积分。


2.2.3、定积分的性质


PS:知道了微分和积分的知识,接下来就是一阶微分、二阶微分、以及积分在图像处理中的应用。
以上是关于微分几何主要研究啥的主要内容,如果未能解决你的问题,请参考以下文章