高等数学：微分积分物理以及几何意义

Posted 2021-08-29 Upupup6

目录

0、前言

1、微分

1.1、一元微分

1.1.1、微分的来由

1.1.2、微分的定义

1.2、多元微分

1.2.1、邻域

1.2.2、重极限

 1.2.3、连续 

 1.2.4、偏导数

1.2.5、全微分

  2、积分

 2.1、定积分

2.1.1、几何背景

 2.2.2、可积性（充分必要条件）

 2.2.3、定积分的性质

0、前言

图像处理中会运用到各种算子，要想搞懂每种算子的使用，首先得有微分积分的基础知识。

1、微分

1.1、一元微分

1.1.1、微分的来由

微分<------------------>近似值<---------------->直线增量去近似代替曲线增量的那个直线增量部分---->记号dy------->y的微分---------->dy=Adx

1.1.2、微分的定义

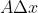 是直线的增量去代替曲线的增量，那么问题来了，A到底是什么东西？

由前边由来可知，A应该是直线的导数，这个直线导数是曲线在该点切线的斜率，因此A应当是导数。

由此推导出来的定理：

在处可微的充分必要条件是在处可导。

可微必可导的证明：

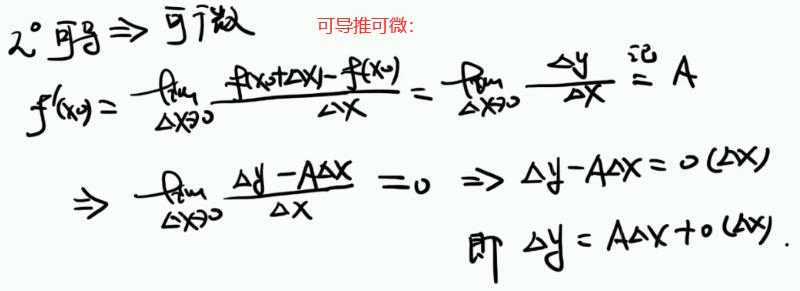
 所以一元函数可导和可微是等价的，但是两者的概念不一样。（可导的概念是变化率，而且是个瞬时变化率；而可微的概念是一个近似代替的问题，能不能用直线增量去近似代替曲线增量的问题）（即可导是一个瞬时变化率的问题，可微是一个近似值，但是他们两个在一元函数里边是相互等价的）

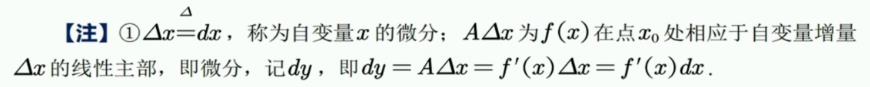
将上式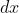左移，

导数和微分的几何意义：

 

 

 

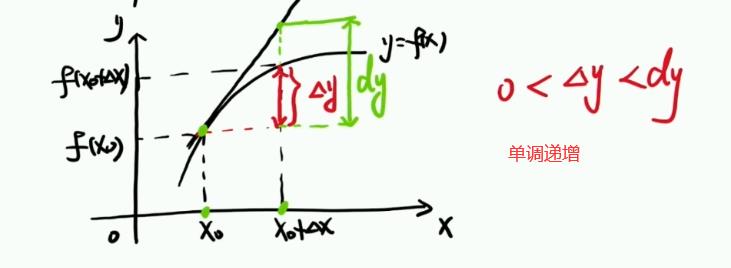
1.2、多元微分

一元与多元的区分就是由原来的一个自变量，变成了多个自变量。 

1.2.1、邻域

邻域概念：第二个趋近于邻域是把中间点p给扣掉(大于0就保证取不到中间点p)。

二元函数的几何意义：其实就是形成了一个二维曲面。

1.2.2、重极限

 

 1.2.3、连续 

 

 1.2.4、偏导数

一元函数导数：

 

多元函数偏导数：

对x偏导数：(对x求偏导，把y看成始终不变的 )

  

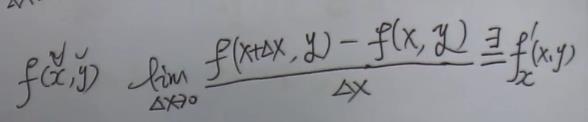
 对y的偏导数：

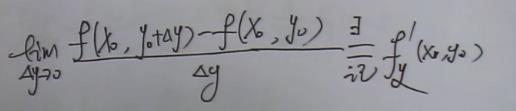
偏导数的几何意义：

 高阶偏导数：

 

 连续指的是混合偏导数连续。

1.2.5、全微分

 

 

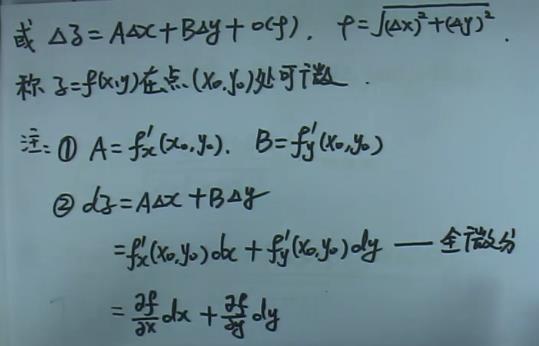
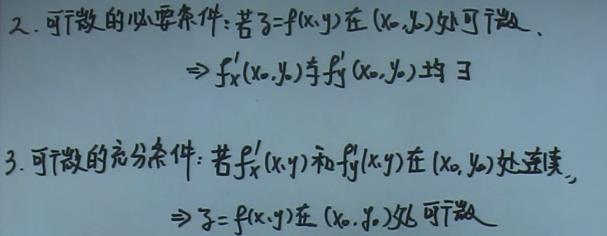
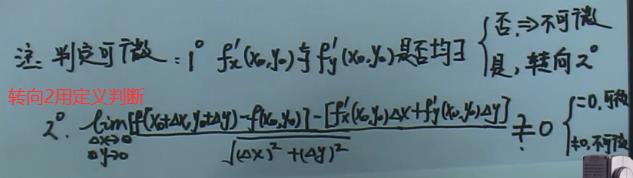
  2、积分

 2.1、定积分

2.1.1、几何背景

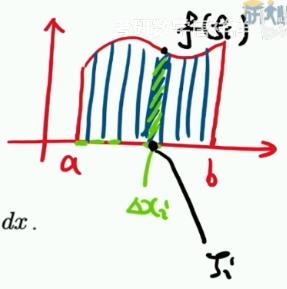
几何背景：就是曲边梯形的面积。曲边梯形的面积(任意划分，看成小矩形的面积)

Q：如何求一个函数与x=a,x=b与x轴所围成的曲边梯形的面积？

A：首先对曲边梯形任意的划分，然后找一个作为代表，把它近似看作一个小矩形，找其宽度 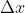，并取一点，找到该点的函数值， 对划分的任意多个小矩形都找一点以及该点对应值，相乘（相当于长和宽）并求和，求和就相当于n个矩形的面积加起来。

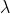趋近于0，每一个区间都有直径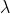，表示n个小区间里边直径的最大值，直径的最大值都趋近于0，保证了你划分的精细程度。

定积分的概念：

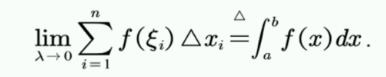
划分、取 点、求和、取极限。

将上述极限值定义为 一元函数y=f(x)在闭区间a到b上的一个定积分(如果  极限存在，并把该极限定义为f(x)在这个区间上的定积分)。

定积分的几何意义：n项和的极限。

 2.2.2、可积性（充分必要条件）

PS：可积一般指定积分。

 2.2.3、定积分的性质

 PS：知道了微分和积分的知识，接下来就是一阶微分、二阶微分、以及积分在图像处理中的应用。