如何求这个一阶线性非齐次方程组的通解,奉上我所有积分
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了如何求这个一阶线性非齐次方程组的通解,奉上我所有积分相关的知识,希望对你有一定的参考价值。
需要关键步骤的过程,谢谢

矩阵分两类, 一类是可以对角化的, 可以用于求解常系数微分方程组.
另一类是不能对角化, 称为亏损矩阵, 例如你这个题目中的系数矩阵就是亏损矩阵.
对于一般的亏损矩阵, 可以转换成标准形.
你这个题目中的矩阵已经与标准形很类似了, 不需要变换. 直接按照楼上解法就可以.
严格的标准形为:

dy1/dx=-y1-y2+x^2
dy2/dx=-y2-y3+2x
dy3/dx=-y3+x
=========================
第三个可以单独解
y3'+y3=x
积分因子=exp(积分 dx)=e^x
e^x y3'+e^xy3=xe^x
(e^x y3)'=xe^x
两边积分
e^x y3=(x-1)e^x+C3
y3=x-1+C3*e^(-x)
=========================
代入第二个方程
y2'+y2=2x-y3
=2x-(x-1)-C3e^(-x)
=x+1-C3e^(-x)
同样的积分因子
(e^x y2)'=(x+1)e^x-C3
两边积分
e^x y2=xe^x-C3x+C2
y2=x-C3x e^(-x)+C2e^(-x)
=========================
再代回第一个方程
y1'+y1=x^2-y2=x^2-x+C3xe^(-x)-C2e^(-x)
同样的积分因子
(e^x y1)'=x^2 e^x -x e^x +C3x-C2
两边积分
e^x y1=(x^2-2x+2)e^x-(x-1)e^x+(C3/2)x^2-C2x+C1
y1=x^2-2x+2-x+1+[(C3/2)x^2-C2x+C1]e^(-x)
=x^2-3x+3+[(C3/2)x^2-C2x+C1]e^(-x)
C1,C2,C3任意常数本回答被提问者和网友采纳 参考技术B 可以用C语言编程求解! 参考技术C 上课没好好听讲吧? 参考技术D 等我翻翻高数课本
高斯消元法求齐次线性方程的通解

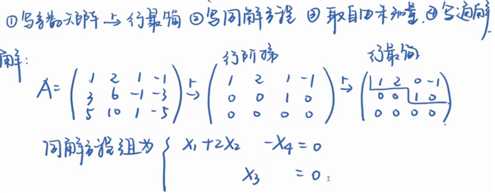
2个方程,2个约束,4个未知量,2个自由未知量
每个台阶首非零元,取为约束未知量


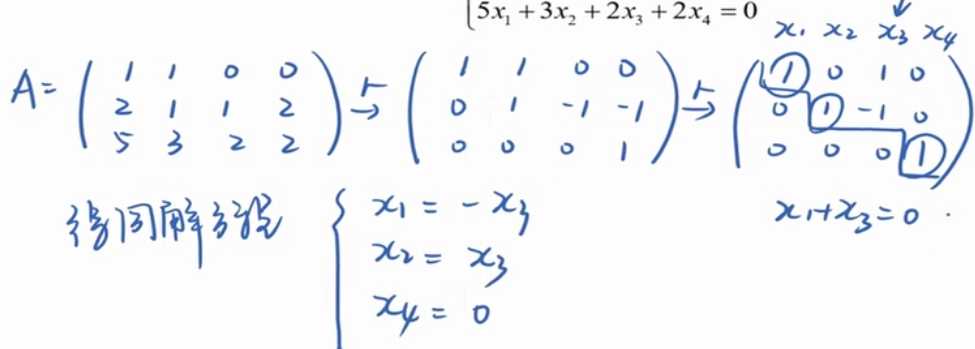


以上是关于如何求这个一阶线性非齐次方程组的通解,奉上我所有积分的主要内容,如果未能解决你的问题,请参考以下文章
《Differential Equations with Boundary-Value Problems》-chaper2-一阶线性方程