matlab 求齐次线性方程组的非零解

Posted 2023-05-12

参考技术A 用
solve
函数，用help自己查看！
如果没记错的话，解法应该是如下格式：
[x1,x2,
...
]
=
solve（'exp1',
'exp2',
...）
几点说明：
1.
exp是指表达式，exp1指第一个表达式，形如
x1+x2-20
,
具体表示“x1+x2-20=0”这个等式
2.
注意
表达式要用
'
'
这个符号引起来，而且将所有变量常量都移到等式左边，右边是
=0
如
x1+x2=y+20
应该化简为
x1
+x2
-y
-20
=0，在solve中的表示为
solve（'x1
+x2
-y
-20
'）

非齐次线性方程组有唯一解怎么求

Ax=0无非零解时.则A为满秩矩阵。则Ax=b一定有解

Ax=0有无穷多解时，则A一定不为满秩矩阵，

Ax=b的解得情况有无解和无穷多解

无解：R(A)≠R(A|b)

无穷解：R(A)等于R(A|b)。且不为满秩

Ax=b无解时，可知Ax=0一定有无穷多解

Ax=b有唯一解时，可知A为满秩矩阵，则Ax=0只有零解

齐次线性方程组，要么零解（R(A)=n），要么无穷解（R(A)<n)

一个零解，一个非零的唯一解.不能同时发生。

扩展资料：

解的存在性

非齐次线性方程组Ax=b 有解的充分必要条件是：系数矩阵的秩等于增广矩阵的秩，即rank(A)=rank(A, b)（否则为无解）。

非齐次线性方程组有唯一解的充要条件是rank(A)=n。

非齐次线性方程组有无穷多解的充要条件是rank(A)<n。（rank(A)表示A的秩）

参考资料来源：百度百科-非齐次线性方程组

参考技术A

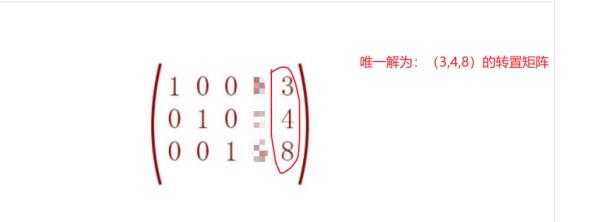
由题目，该方程为非齐次线性方程组，则必有系数矩阵和增广矩阵，求唯一解，则证明非齐次线性方程的增广矩阵满秩，求增广矩阵的行最简形式，则最后一列即为唯一解。

参考技术B 线性代数相关知识。求矩阵的秩，系数矩阵的秩等于增广矩阵的秩时，非齐次线性方程有唯一解；当系数矩阵的秩小于增广矩阵的秩时，无解；当系数矩阵的秩大于增广矩阵的秩的时候，无穷解。本回答被提问者和网友采纳 参考技术C 把增广矩阵左部分（也就是系数矩阵化成行最简）得到右边一列就是唯一解（实际上就是令自由变量为0），解析：比如第一行为（1 0 0 0 a）也就是（X1乘1等于a）那X1就等于a，第二行是X2，类推。 参考技术D 用克拉默法则，可以分别得到x1，x2，x3