在信号与系统中怎样判断微分方程和差分方程是不是为线性系统和因果系统

Posted 2023-05-15

参考技术A 因果 t＜0 系统输出为零
线性 乘个系数输出成比例 具体忘记了书上不是有么

信号与系统 2023（春季） 作业要求 - 第三次作业

◎ 参考资料：

• 信号与系统 2022 春季学期第二次作业
• 信号与系统 2022 春季学期第三次作业
• 信号与系统 2023（春季） 作业要求 - 第三次作业

 

01 基础练习

---

一、从系统框图到方程

  试写出下面各图对应的系统输入输出之间的微分方程和差分方程。请大家注意本题中采用了不同的符号表示了积分、延迟，请大家注意辨识这些不同的表示方法。

本次作业中有一些框图与 信号与系统 2022 春季学期第二次作业 中具有相同的结构，但是相关系数进行了改变，请大家注意区分。

1、必做题

  （1）

▲ 图1.1.1 连续时间系统框图

  （2）

▲ 图1.1.2 离散时间系统框图

  （3）

▲ 图1.1.3 具有双综合器连续时间系统框图

  （4）

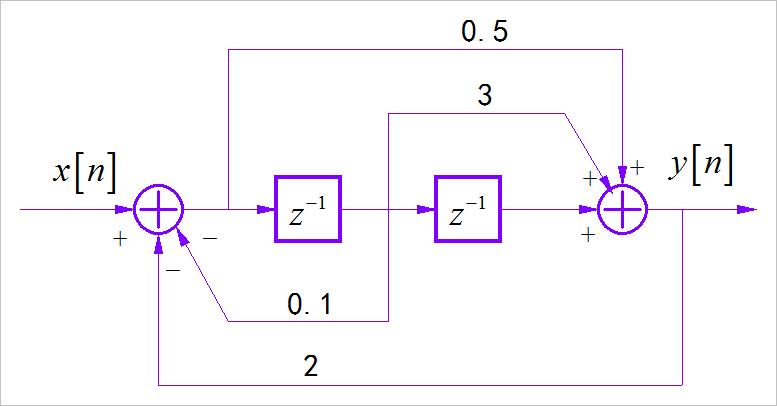
▲ 图1.1.4 具有双综合器的离散时间系统

2、选做题

  （1）

▲ 图1.1.5 具有三个综合器的连续时间系统框图

  （2）

▲ 图1.1.6 FIR离散时间滤波器II型

  （3）

▲ 图1.1.7 FIR离散时间滤波器I型

注： 请对比 （2） （3） 两个小题对应的差分方程是否相同。

二、列写系统微分方程

1、必做题

  对于下电路系统， 输入电压信号为 $e\left(t\right)$ ，输出电压信号为 $u\left(t\right)$ 。 请列些出该电路的输入输出之间的常系数微分方程。

  （1） 电路系统

▲ 图1.2.1 RLC 电路图

  （2） 液体混合

  在某一容器中对 A、B 两种液体进行混合。在第 $n$ 步，把 $x\left[n\right]$ 升液体 A 和 $50-x\left[n\right]$ 升液体 B 都导入容器中，假设 $x\left[n\right]<50$ 。该容器已有 950 升 A 与 B 的混合液。均匀混合后，再从容器中倒出 50 升混合液。如此重复上述过程在第 $n$ 个循环结束后，假设 A 在混合液所占百分比为 $y\left[n\right]$ 。

  （1） 试列写出 $x\left[n\right]$ ， $y\left[n\right]$ 之间的差分方程；
  （2） 如果已知 $x\left[n\right]=20$ ， $y\left[0\right]=0$ ，求解 $y\left[n\right]$ ；
  （3） 指出期中的自由分量和强迫分量；
  （4） 当 $n\to \infty$ 时， $y\left[\infty \right]=?$

▲ 图1.2.2 溶液混合过程

2、选做题

  下图所示为理想火箭推动器模型。火箭质量为 $m_1$ ，载荷仓质量为 $m_2$ 。两者中间 使用弹簧系数为 $k$ 的弹簧连接。火箭和载荷仓各自收到摩擦力的作用。摩擦系数分别为 $f_1$ 、 $f_2$ 。

  （1） 火箭推动模型

▲ 图1.2.3 火箭实验系统

  求火箭推理 $e_1\left(t\right)$ 与载荷仓运动速度 $v_2\left(t\right)$ 之间的微分方程。

提示：分别对火箭与载荷仓的受力进行分析，根据牛顿第三定理，列写它们各自的动力学方程。它们之间所受到的弹簧力大小相等，方向相反，并与它们之间的距离（等于它们速度差的积分）成正比。根据列出的三个方程进行化简得到输入作用力 $e_1\left(t\right)$ 与载荷仓运动速度 $v_2\left(t\right)$ 之间的微分方程。

▲ 图1,2,4 火箭与载荷仓受力分析

三、微分方程、差分方程求解

1、必做题

  （1） 微分方程求解

  已知LTI系统输入输出之间的微分方程如下：

  输入信号为：

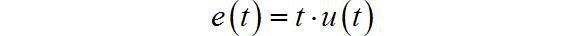
  系统起始状态为：

  分别求出：
  （1） 系统的完全响应；
  （2） 指出响应中的零输入响应、零状态响应、自由响应、强迫响应，瞬态响应、稳态响应等各分量；
  （3） 求解该系统的单位冲激响应， 单位阶跃响应；

提示： （1） 根据奇异函数匹配方法求解系统 $0_{+}$ 时刻的初始条件来求解完全响应中齐次解待定系数的求解； （2） 自行验证第三小问中的单位冲激响应与单位阶跃响应之间的微分关系。

  （2）差分方程求解

  已知离散时间系统对应的二阶后向差分方程如下：

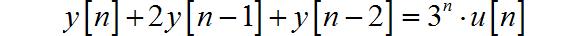
  初始条件为：

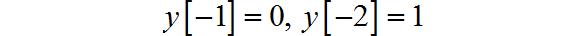
  （1） 求出该系统的完全解；
  （2）分别指出系统的自由响应、强迫响应、瞬态响应、稳态响应；
  （3）求出系统的零输入响应、零状态响应；

2、选做题

  （1） 求解系统的单位冲激响应

  已知 LTI 系统对应的微分方程为：

  求解该系统的单位冲激响应。

  （2） 求系统的单位冲激响应

  已知 LTI 系统输入输出之间对应的微分方程为：

其中：

  求该系统的单位冲激响应： $h\left(t\right)$ 。

提示： 上面方程右边包括有系统的输入信号 $x\left(t\right)$ 与 $f\left(t\right)$ 的卷积以及 $-x\left(t\right)$ 部分。根据单位冲激响应的定义， 把 $x\left(t\right)=\delta \left(t\right)$ 代入方程右边之后便可以得到关于输出信号的微分方程， 求解之后便可以得到系统的单位冲激响应。

四、系统分析

1、必做题

  有一系统在激励信号为 $e_1\left(t\right)=u\left(t\right)$ 时完全响应为：$$r_1\left(t\right)=2e^{-t}u\left(t\right)$$当激励变为： $e_2\left(t\right)=\delta \left(t\right)$ 时完全响应为：$$r_2\left(t\right)=\delta \left(t\right)$$。

  （1） 求该系统的零输入响应的： $r_{zi}\left(t\right)$ ；
  （2） 系统的其实状态不变，求其对激励为 $e_3\left(t\right)=e^{-t}u\left(t\right)$ 时的完全响应 $r_3\left(t\right)=?$

提示：
求解第一问：将完全响应分解成对应的零输入响应和零状态响应。在两次输入信号下分别为 $u\left(t\right),\delta \left(t\right)$ 作用下，对应的零输入相应的分量 $r_{zi}\left(t\right)$ 保持不变；而两次零状态响应 $r_{zs1}\left(t\right),r_{zs2}\left(t\right)$ 之间满足微分关系： $r_{zs1}^{\prime }\left(t\right)=r_{zs2}\left(t\right)$ 。因此可以有：$$r_1\left(t\right)=数字信号处理线性常系数差分方程\; (\; “\; 线性常系数差分方程\; “\; 与\; “\; 线性时不变系统\; “\; 关联\; |\; 根据\; “\; 线性常系数差分方程\; “\; 与\; “\; 边界条件\; “\; 确定系统是否是\; 线性时不变系统方法\; )$$

数字信号处理线性常系数差分方程 ( 根据 “ 线性常系数差分方程 “ 与 “ 边界条件 “ 确定系统是否是 “ 线性时不变系统 “ 案例 | 根据 “ 线性时不变系统 “ 定义证明 )

数字信号处理线性常系数差分方程 ( 根据 “ 线性常系数差分方程 “ 与 “ 边界条件 “ 确定系统是否是 “ 线性时不变系统 “ 案例 | 使用递推方法证明 )

数字信号处理线性常系数差分方程 ( 根据 “ 线性常系数差分方程 “ 与 “ 边界条件 “ 确定系统是否是 “ 线性时不变系统 “ 案例二 | 修改边界条件 | 使用递推方法证明 )

[离散时间信号处理学习笔记] 4. 线性常系数差分方程

数字信号处理线性常系数差分方程 ( 线性常系数差分方程 与 边界条件 总结 ) ★★★