陈省身：三角形内角和不等于180°

Posted 2022-12-06 数据与算法之美

全世界只有3.14 % 的人关注了

爆炸吧知识

三角形

外角和为360°

作为公认的劳模，平日里，超模君不但要码字，工作之余还要监督表妹做作业，也难怪表妹成绩总是能名列前茅。

今天表妹做作业时，遇到一道判断题：“三角形的内角和等于180°”，她毫不犹豫打了勾。

超模君告诉表妹，这道题你可以打勾，但也要知道这个说法是不完全正确的。

表妹急了，怎么会呢？课本上明明说“三角形的内角和等于180°”，而且老师上课还再三强调大家一定要记住这个定理呢。

为了从小培养表妹严谨的科研精神，超模君决定给她上一课！

三角形的外角和为360°

我们从小就滚瓜烂熟的“三角形的内角和等于180°”这种数学常识其实是不严谨的。我们先从伟大的华人数学家陈省身的一场讲学说起。

那是1980年，陈省身教授受邀在北京大学的一次讲学中语惊四座：“人们常说，三角形内角和等于180°。但是，这是不对的！”

当时现场一片哗然，目瞪口呆，三角形内角和等于180°不是数学常识吗？怎么回事？

紧接着，陈教授就大家的疑惑作出了精彩的解答：

说“三角形内角和为180°”不对，不是说这个事实不对，而是说这种看问题的方法不对，应当 说“三角形外角和是360°”！

把眼光盯住内角，只能看到：

三角形内角和是180°；

四边形内角和是360°；

五边形内角和是 540°；

......

n边形内角和是（n－2）×180°。

这就找到了一个计算内角和的公式，公式里出现了边数n。

如果看外角呢？

三角形的外角和是360°；

四边形的外角和是360°；五边形的外角和是360°；

……

任意n边形外角和都是360°。

这就把多种情形用一个十分简单的结论概况起来了。用一个与n无关的常数代替了与n有关的公式，找到了更一般的规律。

在这次讲学中，陈教授给我们传递了一个观点：数学不是罗列更多的现象，也不是追求更妙的技巧，而是要从更普遍的、更一般的角度寻求规律和答案。

不只盯着多边形的内角看，用一个与n无关的常数代替了与n有关的公式，可找到了更一般的规律：任意n边形的外角和都是360°。

下面举个例子，简单证明任意n边形的外角和都是360°这个规律。

假设一只蚂蚁在多边形的边界上绕圈子（如下图）。每经过一个顶点，它前进的方向就要改变一次，改变的角度恰好是这个顶点处的外角。爬了一圈，回到原处，方向和出发时一致了，角度改变量之和当然恰好是360°。

这样看问题，给“任意多边形外角和等于360°”这条普遍规律找得到了直观上的解释。

陈教授在那次讲学中，没有否定“三角形的内角和等于180°”，因为其中涉及欧式几何和非欧几何。

三角形的内角和不一定等于180°

“三角形的内角和等于180°”是从欧式几何里的公理五（又称之为平行公设）衍生出来的公理。在欧式几何里，“三角形的内角和等于180°”是正确的。

下面简单证明一下”三角形的内角和等于180°“的一般规律：

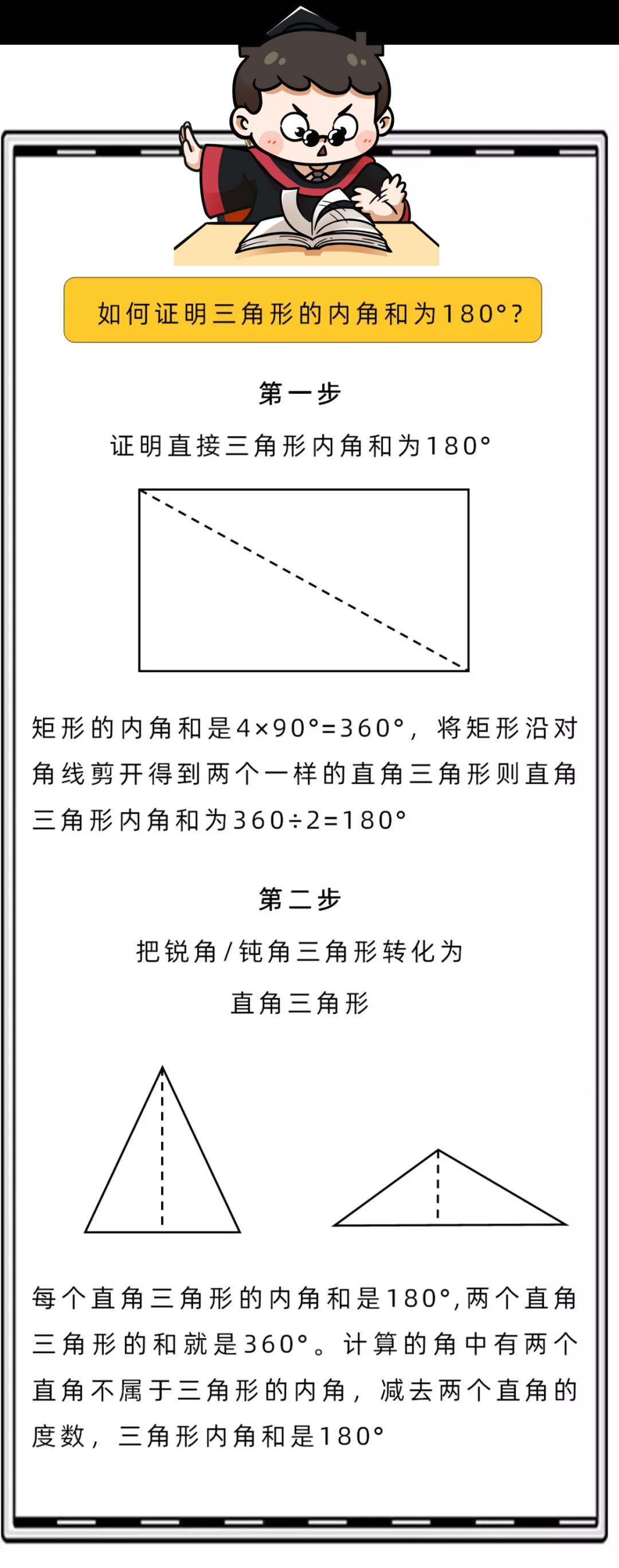
随着数学研究的进步，到了高斯时代，欧氏几何里的公理五备受质疑。

俄罗斯数学家罗巴切夫斯基、匈牙利人波尔约表示：第五公理只是公理系统的一种可能选择，并非必然的几何真理，即“三角形的内角和不一定等于180°”，从而发现非欧几里得的几何学，即非欧几何。

举个例子，地球的赤道、0 度经线和 90 度经线相交构成一个“三角形”，这个“三角形”的三个角都应该是 90°，它们的和就是 270°！

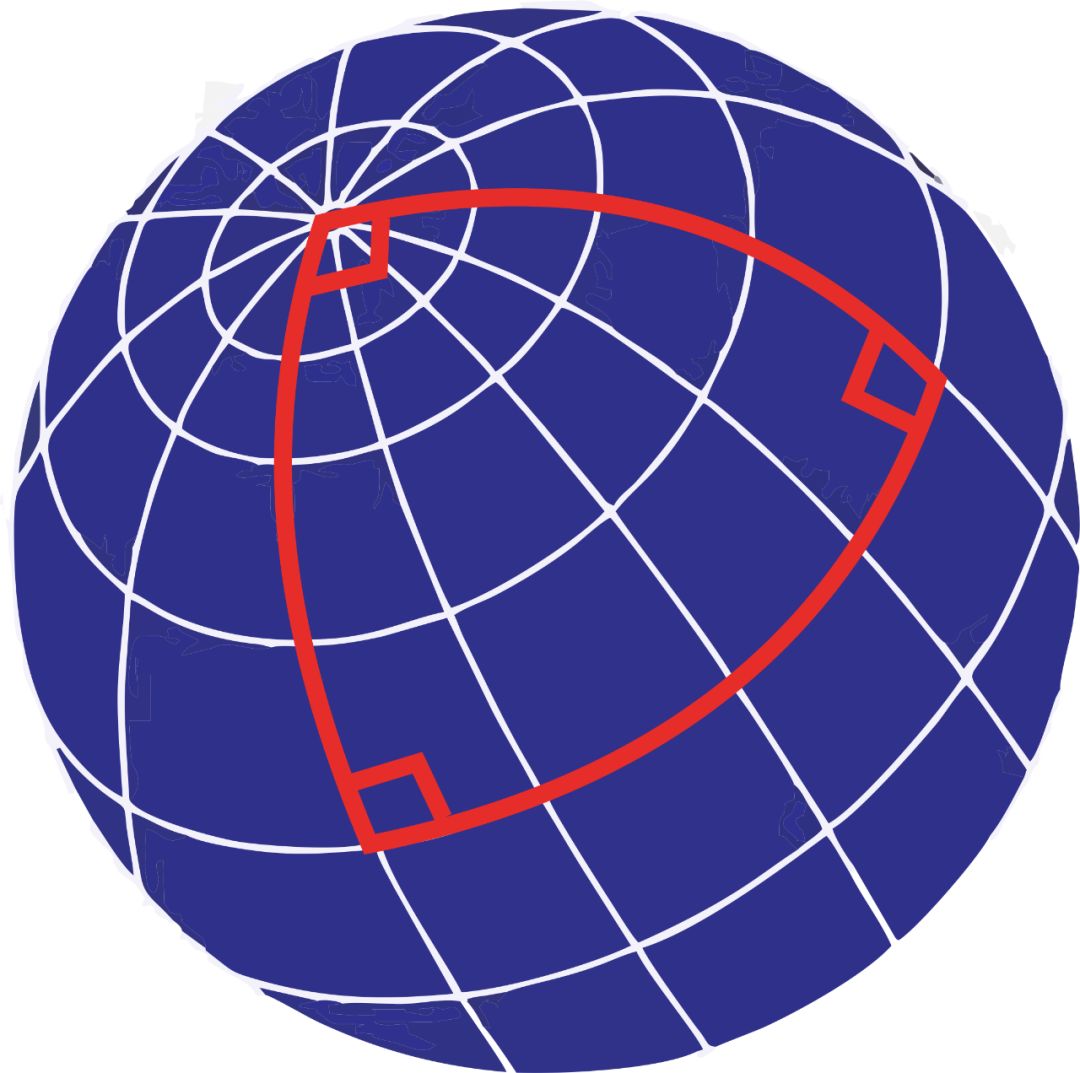
相反，在凹面上的三角形内角和自然小于180°，所以在非欧几何里，三角形的内角和不一定等于180°。

那些有趣的三角形

我们的生活中存在着许多有趣的三角形，他们的内角和或大于180°，或小于180°，有的还被人们巧妙得利用到各个领域。

比如，可以用作运输的莱洛三角形：

谢尔宾斯基三角形：一个正三角形，挖去一个“中心三角形”（即以原三角形各边的中点为顶点的三角形），在剩下的小三角形中又挖去一个“中心三角形”，如此无限循环，谢尔宾斯基三角形面积越趋近于零，而它的周长越趋近于无限大。

三维世界不存在的彭罗斯三角形：彭罗斯三角形被称为“最纯粹形式的不可能”，它将三个不同角度的三角顶角整合为一个整体，因而本应是一个平面的面发生了扭转，这样的三角形在三维世界是不可能存在的。

这样的“三角形”被艺术家巧妙地用在作品中，比如世界名画：埃舍尔的《瀑布》。

《瀑布》

还有澳大利亚东珀斯的地标建筑就是彭罗斯三角形的模型。

澳大利亚东珀斯彭罗斯三角形

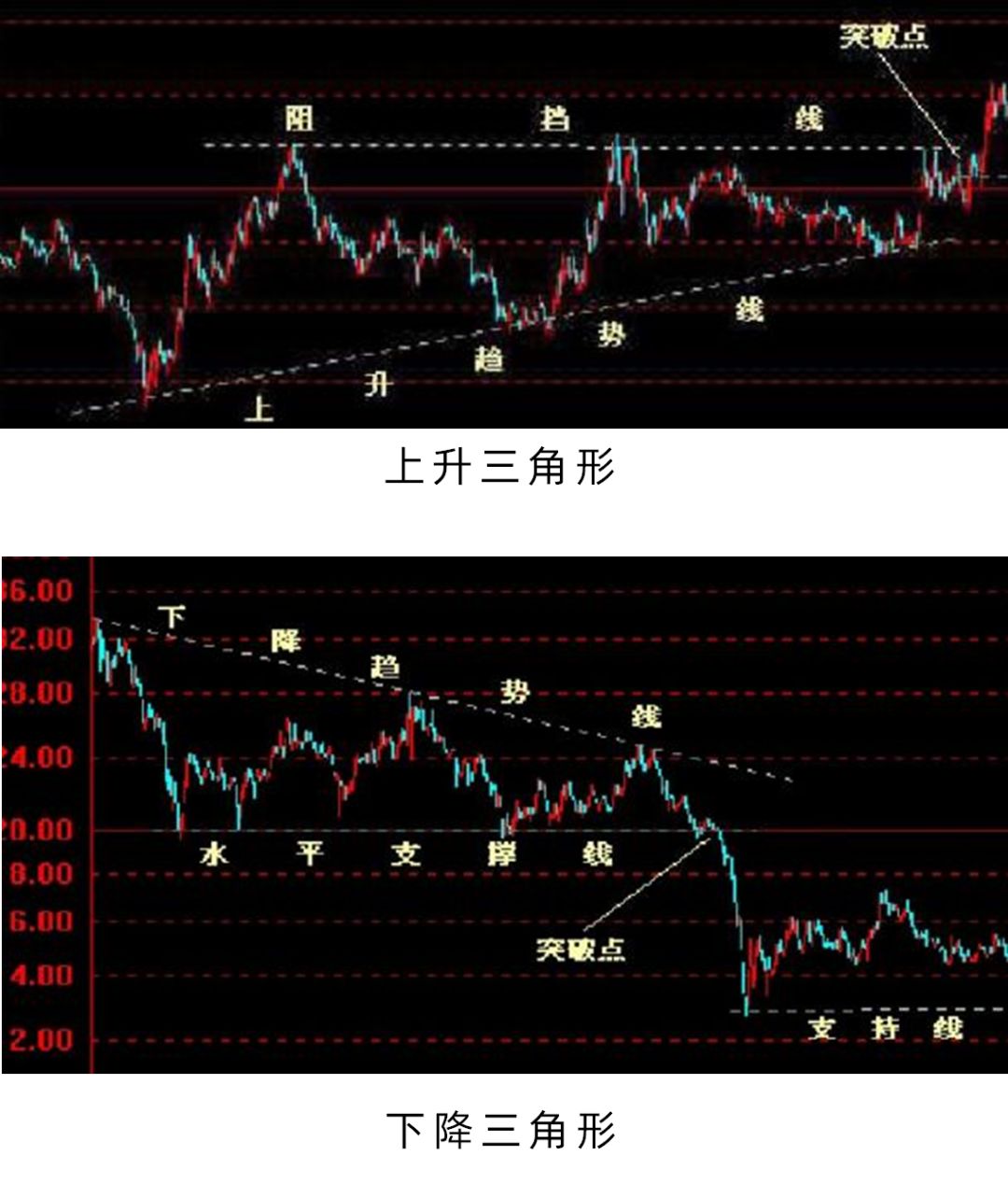
股民眼中的三角形：三角形整理突破分析是高阶股民必备的技能。

程序员眼中的三角形：行吧，在程序员的世界里，什么都是字母加数字的。

非欧几何应用

回到开头和表妹讲的题目：三角形内角和等于180°的对与错。其实在小学里，学的默认是欧式几何，所以是正确的。然而在非欧几何里，三角形的内角和等于180°就不成立了。

非欧几何的应用在生活中和欧式几何一样十分常见，如在航海学上：地球本身就是曲面的，如果使用欧式几何，只会得到错误的结论。

图来源于B站肉兔君

近代黎曼几何学在广义相对论里得到了重要的应用。物理学家爱因斯坦的广义相对论中的空间几何就是黎曼几何。

爱因斯坦在看到了罗巴切夫斯基和黎曼的发现之后，在广义相对论里，放弃了关于时空均匀性的观念，他认为时空是弯曲的。非欧几何成了解释相对论的数学工具。

数学的意义就在于，它经常走在其他科学的前面，我们通过数学的研究，可以为其他科学提供很多帮助。

即使学数学会让人头凉凉的，依然有人抱着“我不秃谁秃”的死士精神走在数学研究的道路上。

所以这一杯，敬所有爱数学的人儿。

另外，表妹你懂了嘛？

写在最后

知识，才是不可战胜的。

知识带来的底气，是最高级的勇气。关注超模君新推出的同理可得数学文化衫，让你酷拽一夏天。

同理可得数学文化衫

  原价158  

  现价128 

数量有限 先到先得

作者简介：超模君，数学教育与生活自媒体博主，新晋理工科奶爸。出版过《芥子须弥 · 大科学家的小故事》；《数学之旅·闪耀人类的54个数学家》。后续数学文化创意多多，欢迎关注认识！

本文系网易新闻·网易号“各有态度”特色内容

部分资料来源于网络

转载请在公众号中，回复“转载”

点这里????关注我，记得标星～