《算法零基础100讲》(第61讲) 前缀和 二维前缀和
Posted 英雄哪里出来
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了《算法零基础100讲》(第61讲) 前缀和 二维前缀和相关的知识,希望对你有一定的参考价值。
零、写在前面
这是《算法零基础100讲》 专栏打卡学习的第六十一天了。
每天打卡的题,做不出来没关系,因为困难的题涉及知识点较多,后面还是会开放出来的,就像昨天的 最大公约数 那道题今天还是会有,所以不要着急,内容能看懂,能自己分析,能做出简单题,就可以打卡。
在刷题的过程中,总结自己遇到的坑点,写出 「 解题报告 」 供他人学习,也是一种自我学习的方式。这就是经典的帮助他人的同时,成就自己。目前, 「 万人千题 」 社区 每天都会有五六篇高质量的 「 解题报告 」 被我 「 加精 」。如果觉得自己有能力的,也可以来发布你的 「 解题报告 」。千万级流量,你我共同拥有。
一、概念定义
有关一维前缀和的概念,在《算法零基础100讲》(第57讲) 前缀和(一) 线性前缀和入门 中已经较为清晰的阐述,今天我们来学习二维的情况。
1、预处理
问题的起源就是对一个矩阵,如何在最快的时间内,求出它的某个子矩阵的和。我们首先把问题简化,对于一个
n
×
m
n \\times m
n×m 的矩阵
A
A
A,如何快速求出
∑
i
=
0
a
∑
j
=
0
b
A
[
i
]
[
j
]
\\sum_i=0^a \\sum_j=0^b A[i][j]
i=0∑aj=0∑bA[i][j] 即求出图中红色部分的元素和。
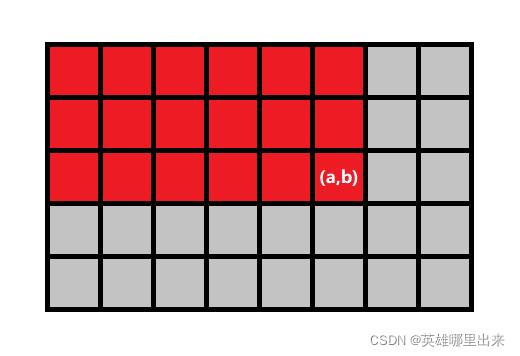
如何快速求出红色部分的和你?我们看下面这个图:
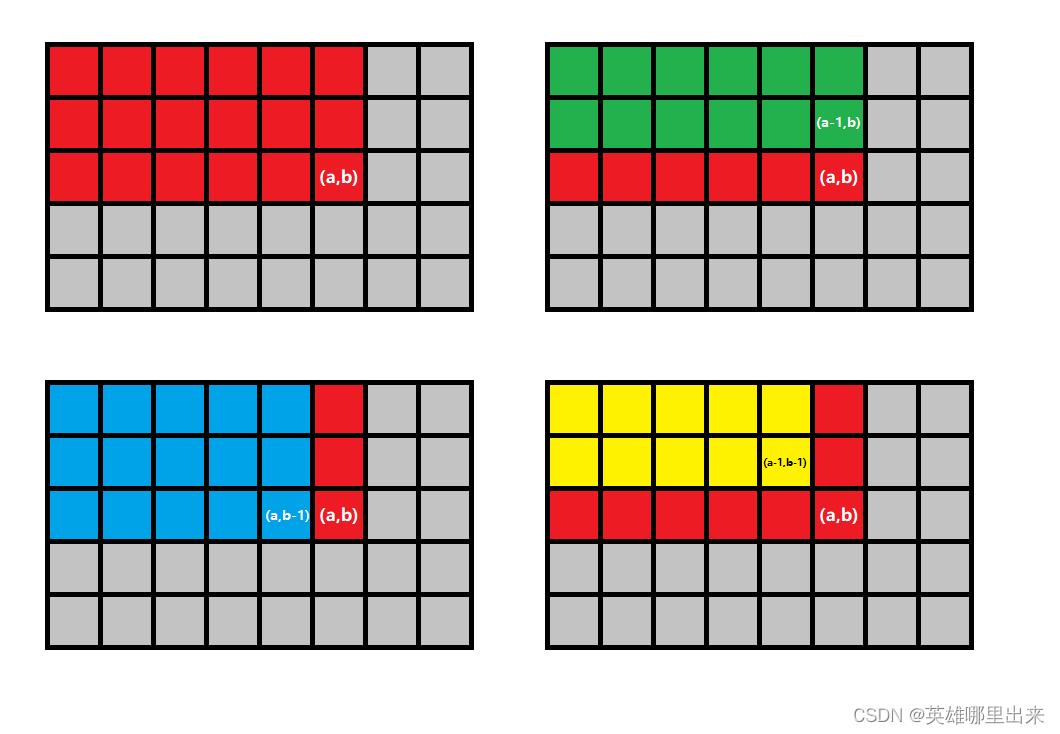
在求红色部分的和时,我们确保 绿色部分、蓝色部分、黄色部分的和都已经求出来了,则可以通过以下公式直接求解:红色部分 =
A
[
a
]
[
b
]
A[a][b]
A[a][b]
+
+
+ 绿色部分
+
+
+ 蓝色部分
−
-
− 黄色部分
如果我们把
∑
i
=
0
a
∑
j
=
0
b
A
[
i
]
[
j
]
\\sum_i=0^a \\sum_j=0^b A[i][j]
∑i=0a∑j=0bA[i][j]表示成另一个矩阵
S
[
a
]
[
b
]
S[a][b]
S[a][b],则可以得到如下递推式:
S
[
a
]
[
b
]
=
A
[
a
]
[
b
]
+
S
[
a
−
1
]
[
b
]
+
S
[
a
]
[
b
−
1
]
−
S
[
a
−
1
]
[
b
−
1
]
S[a][b] = A[a][b] + S[a-1][b] + S[a][b-1] - S[a-1][b-1]
S[a][b]=A[a][b]+S[a−1][b]+S[a][b−1]−S[a−1][b−1]
最后,需要考虑边界情况,即
a
a
a 和
b
b
b 都为 -1 的情况,得到递推式如下:
S
[
a
]
[
b
]
=
0
a
=
−
1
0
b
=
−
1
A
[
a
]
[
b
]
+
S
[
a
−
1
]
[
b
]
+
S
[
a
]
[
b
−
1
]
−
S
[
a
−
1
]
[
b
−
1
]
o
t
h
e
r
w
i
s
e
S[a][b] = \\begincases 0 & a=-1 \\\\ 0 & b=-1 \\\\ A[a][b] + S[a-1][b] + S[a][b-1] - S[a-1][b-1] & otherwise\\endcases
S[a][b]=⎩⎪⎨⎪⎧00A[a][b]+S[a−1][b]+S[a][b−1]−S[a−1][b−1]a=−1b=−1otherwise
2、预处理代码实现
实际在计算的过程,数组下标无法是负数,所以,我们可以将数组偏移一个位置,当然如果不偏移,就要对下标进行特殊处理,如下:
void calcSum(int sum[maxn][maxn], int r, int c, int **mat)
int i, j;
for(i = 0; i < r; ++i)
for(j = 0; j < c; ++j)
if(i == 0)
if(j == 0)
sum[i][j] = mat[i][j];
else
sum[i][j] = mat[i][j] + sum[i][j-1];
else
if(j == 0)
sum[i][j] = mat[i][j] + sum[i-1][j];
else
sum[i][j] = mat[i][j] + sum[i-1][j] + sum[i][j-1] - sum[i-1][j-1];
3、查询
给定一个
n
×
m
n \\times m
n×m 的矩阵,然后
Q
Q
Q 次查询,每次查询都是
(
r
1
,
c
1
,
r
2
,
c
2
)
(r_1, c_1, r_2, c_2)
(r1,c1,r2,c2),求子矩阵的和。
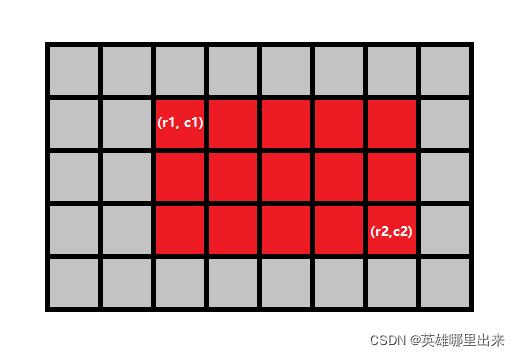
同样可以采用之前的思路,得到矩形和如下:
S
[
r
2
]
[
c
2
]
−
S
[
r
1
−
1
]
[
c
2
]
−
S
[
r
2
]
[
c
1
−
1
]
+
S
[
r
1
−
1
]
[
c
1
−
1
]
S[r_2][c_2] - S[r_1-1][c_2] - S[r_2][c_1-1] + S[r_1-1][c_1-1]
S[r2][c2]−S[r1−1][c2]−S[r2][c1−1]+S[r1−1][c1−1]
4、查询代码实现
为了把下标为负数的情况单独抽出来,我们用一个函数getSum来实现:
int getSum(int sum[maxn][maxn], int r, int c)
if(r == -1 || c == -1)
return 0;
return sum[r][c];
int getSum2(int sum[maxn][maxn], int r1, int c1, int r2, int c2)
return getSum(sum, r2, c2) - getSum(sum, r1-1, c2) - getSum(sum, r2, c1-1) + getSum(sum, r1-1, c1-1);
二、题目描述
给你一个二维矩阵
matrix和一个整数 k k k ,矩阵大小为 n × m n \\times m n×m 由非负整数组成。矩阵中坐标 ( a , b ) (a, b) (a,b) 的 值 可由对所有满足 0 ≤ i ≤ a < n 0 \\le i \\le a \\lt n 0≤i≤a<n 且 0 ≤ j ≤ b < m 0 \\le j \\le b < m 0≤j≤b<m 的元素 m a t r i x [ i ] [ j ] matrix[i][j] matrix[i][j] (下标从 0 开始计数) 执行异或运算得到。
三、算法详解
异或运算的性质,已经在 (第46讲) 位运算 (异或) 入门 讲过,它同样满足前缀和的性质。所以可以直接采用前缀和算法求出所有的数,然后放到一个数组中,并且递减排序后,取第 k − 1 k-1 k−1 个数就是答案了。
四、源码剖析
#define maxn 1010
void calcSum(int sum[maxn][maxn], int r, int c, int **mat)
int i, j;
for(i = 0; i < r; ++i)
for(j = 0; j < c; ++j)
if(i == 0)
if(j == 0)
sum[i][j] = mat[i以上是关于《算法零基础100讲》(第61讲) 前缀和 二维前缀和的主要内容,如果未能解决你的问题,请参考以下文章
《算法零基础100讲》(第60讲) 前缀和 线性前缀和配合哈希表
题解《算法零基础100讲》(第10讲) 因子分解和枚举(java版)