《算法零基础100讲》(第59讲) 前缀和 线性前缀和统计

Posted 2022-01-08 英雄哪里出来

文章目录

• 零、写在前面
• 一、概念定义
• • 1、问题引入
  • 2、最坏时间复杂度
  • 3、优化算法
• 二、题目描述
• 三、算法详解
• 四、源码剖析
• 五、推荐专栏
• 六、习题练习

零、写在前面

  这是《算法零基础100讲》 专栏打卡学习的第五十九天了。
  每天打卡的题，做不出来没关系，因为困难的题涉及知识点较多，后面还是会开放出来的，就像昨天的 最大公约数 那道题今天还是会有，所以不要着急，内容能看懂，能自己分析，能做出简单题，就可以打卡。
  在刷题的过程中，总结自己遇到的坑点，写出 「 解题报告 」 供他人学习，也是一种自我学习的方式。这就是经典的帮助他人的同时，成就自己。目前， 「 万人千题 」 社区 每天都会有五六篇高质量的 「 解题报告 」 被我 「 加精 」。如果觉得自己有能力的，也可以来发布你的 「 解题报告 」。千万级流量，你我共同拥有。

一、概念定义

  有关前缀和的概念，在《算法零基础100讲》(第57讲) 前缀和(一) 线性前缀和入门 中已经较为清晰的阐述，今天我们来学习它的一些应用。

1、问题引入

  考虑这么一个问题，一开始我们有一个下标从零开始的整数区间，区间里的每个格子的值都为0，如下：

然后，我们选择一个区间 $[1,5]$，对区间内的每个值都加上 3，变成：

再选择一个区间 $[3,6]$，对区间内的每个值都加上 2，变成：

最后，求每个格子对应的值是多少。对于这么一个问题，我们来分析一下。

2、最坏时间复杂度

  假设区间的长度为 $n$，总共 $m$ 才累加操作，那么最坏情况下就是每次操作都需要对 $n$ 个数进行累加。所以，朴素算法下，最坏的时间复杂度为 $O(mn)$。

3、优化算法

  当选择区间 $[l,r]$ 累加一个值 $x$ 时，我们可以在 $l$ 的格子加上 $x$，在 $r+1$ 的格子减去 $x$。例如，在 $[1,5]$ 累加 3 这个操作可以简化成在 $1$ 的位置累加 3，而在 $5+1=6$ 的位置减去 3，如下所示：

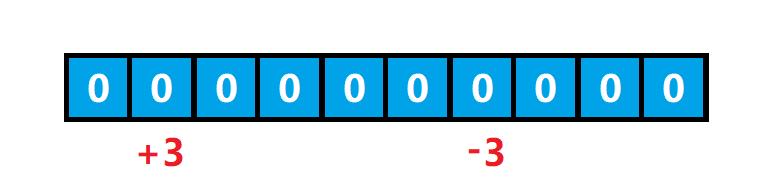
  这样就把每次区间操作的 $O(n)$ 转换成了 $O(1)$。
  最后，统计一次前缀和，就是我们要求的每个格子的累加和了。

二、题目描述

  这里有 $n$ 个航班，它们分别从 $1$ 到 $n$ 进行编号。有一份航班预订表 $bookings$ ，表中第 $i$ 条预订记录 $bookings[i]=[firs{t}_i,las{t}_i,seat{s}_i]$ 意味着在从 $firs{t}_i$ 到 $las{t}_i$ 的 每个航班 上预订了 $seat{s}_i$ 个座位。请你返回一个长度为 $n$ 的数组，里面的元素是每个航班预定的座位总数。

三、算法详解

  对于每个区间，$[firs{t}_i,las{t}_i]$，直接在 $firs{t}_i$ 的位置加上 $seat{s}_i$，并且在 $las{t}_i+1$ 的位置减去 $seat{s}_i$，最后一次前缀和统计就是答案。

四、源码剖析

int* corpFlightBookings(int** bookings, int bookingsSize, int* bookingsColSize, int n, int* returnSize)
    int *sum = (int *)malloc(sizeof(int) * (n+2));
    int *ret = (int *)malloc(sizeof(int) * (n+2));
    int i;
    int f, l, s;
    memset(sum, 0, sizeof(int) * (n+2));
    for(i = 0; i < bookingsSize; ++i) 
        f = bookings[i][0];
        l = bookings[i][1];
        s = bookings[i][2];
        sum[f] += s;                   // (1)
        sum[l+1] -= s;                 // (2)
    
    *returnSize = 0;
    for(i = 1; i <= n; ++i) 
        if(i>1)
            sum[i] += sum[i-1];        // (3)
        ret[ (*returnSize)++ ] = sum[i];
    
    return ret;

• $(1)$ 左区间的位置加上 $s$；
• $(2)$ 右区间+1 的位置减去 $s$；
• $(3)$ 统计前缀和就是答案；

五、推荐专栏

🌳《画解数据结构》🌳
画解顺序表

六、习题练习

序号	题目链接	难度
1	连续的子数组和	★★☆☆☆
2	子数组和排序后的区间和	★★☆☆☆
3	可获得的最大点数	★★☆☆☆
4	有序数组中差绝对值之和	★★☆☆☆
5	航班预订统计	★★☆☆☆

👇🏻 添加 博主 参加九日集训👇🏻