题解《算法零基础100讲》(第12讲) 因子和&&（第13讲 --- 第一题）最大公约数（java版）

Posted 2021-12-05 敲代码的xiaolang

😁算法小白欢迎加入此社区：https://bbs.csdn.net/forums/hero?category=0
由英雄大佬带领的抱团学算法队伍，从0开始，期待你的加入🥳

本博文是对以下文章习题所作的题解，如有不足，请多指教：https://blog.csdn.net/WhereIsHeroFrom/article/details/120875424
https://blog.csdn.net/WhereIsHeroFrom/article/details/121092685

题解：
12讲题目：
https://leetcode-cn.com/problems/four-divisors/

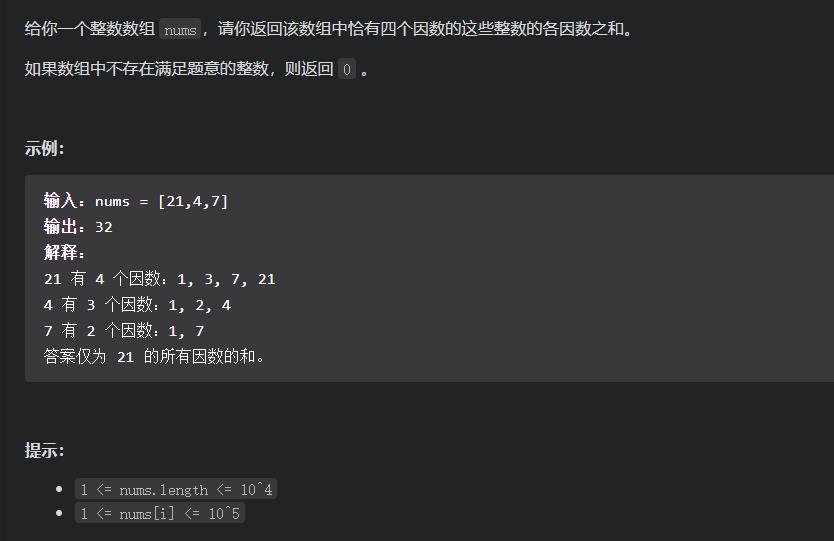
想法就是直接枚举，遍历数组里面的每一个元素，当找到一个因子的时候，让因子的个数加一，如果 i * i !=num，也就是说，此时还有另外一个因子，所以此时因子的个数再加一，直到因子的个数是4的时候，停止操作，然后把所求的和返回。

class Solution {
    public int sumFourDivisors(int[] nums) {
        int answer = 0;
        int i;
        for (int num : nums) {
            int number = 0, sum = 0;
            for (i = 1; i*i <= num; ++i) {
                if (num % i == 0) {
                    number++;
                    sum = sum + i;
                    if (i*i != num) {   
                        number++;
                        sum += num/i;
                    }
                }
            }
            if(number==4) {
                answer = answer + sum;
            }
        }
        return answer;
    }
}

13讲第一题：
https://leetcode-cn.com/problems/find-greatest-common-divisor-of-array/

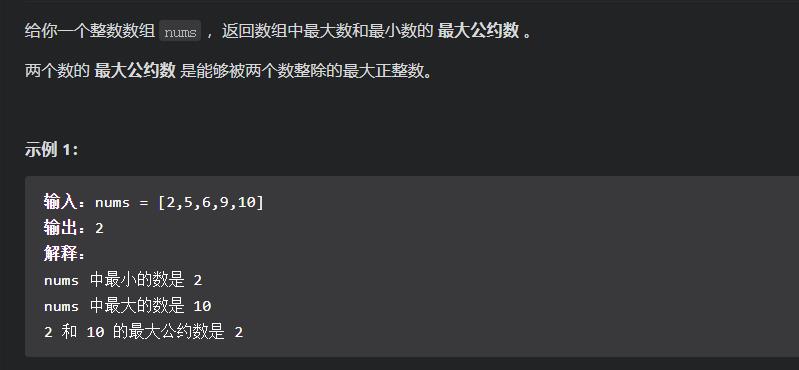
思路很简单，求出最值之后，再进行最大公约数求解。

class Solution {
    public int findGCD(int[] nums) {
        int maxNum = Arrays.stream(nums).max().getAsInt();
        int minNum = Arrays.stream(nums).min().getAsInt();
        int num = gcd(minNum, maxNum);
        return num;
    }
    int gcd(int minNum, int maxNum) {
        int i;
        for(i = minNum; i >= 2; i--) {
        if(minNum % i == 0 && maxNum % i == 0)
            return i;
    }
    return 1;
}
}

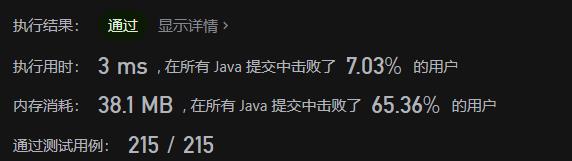
显然，太慢了。。。。

class Solution{
    public int findGCD(int[] nums){
        int i;
        int max = nums[0];
        for(i = 1; i<nums.length; i++){
            if(nums[i] > max){
                max = nums[i];
            }
        }
        int min = nums[0];
        for(i = 1; i<nums.length; i++){
            if(nums[i] < min){
                min = nums[i];
            }
        }
        int num = gcd(min, max);
        return num;
    }
        int gcd(int min, int max) {
        int i;
        for(i = min; i >= 2; i--) {
        if(min % i == 0 && max % i == 0)
            return i;
    }
    return 1;
}
}

使用for循环分别求最大最小值，然后再求最大公约数。

有问题欢迎留言，欢迎加入“万人千题”社区，在这里一起努力。