[计算机数值分析]二分查找求根法

Posted 2022-01-10 Spring-_-Bear

问题描述

给定一个闭区间，我们假设函数f(x)在该区间内有且仅有一个零点，则令f(x) = 0，在该区间内不断折半区间，根据有根的判别条件f(x₁) × f(x₂) < 0,则经过不断地折半，我们总能找到一个给定了精度的根，并且有理由相信，该根x关于精度是 “准确” 的。在实际操作过程中，我们用在精度控制下找到有根区间的中点的值作为方程的近似解。

例：用二分法求方程x³ - x - 1 = 0 在区间[1,1.5]内的一个实根，要求误差不超过0.005。

运行示例

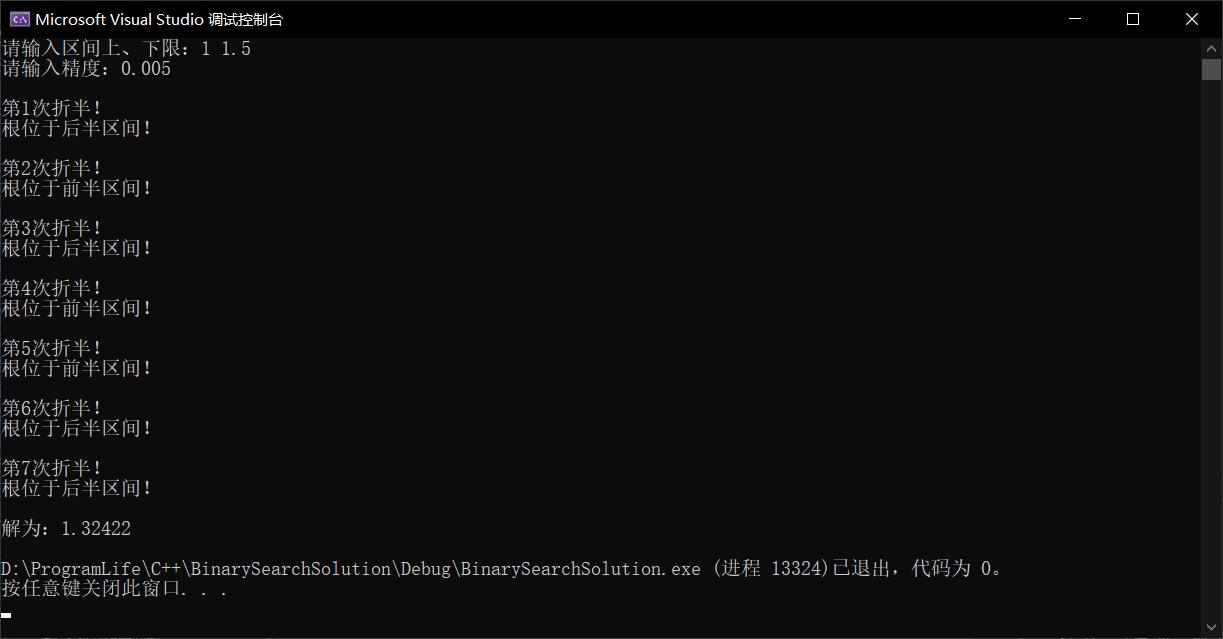
源码

//实现用二分查找求根法：求出给定精度给定方程的根
#include<iostream>
#include<cmath>
using namespace std;

//函数名：function
//参数：用户输入的值x
//返回值：输入参数值的函数值
//功能：求解给定值的函数值
double function(double x)   //用户自定义的函数，可修改

	double result;
	//求解自定义函数值的函数
	result = pow(x, 3) - x - 1;
	return result;


int main(void)

	double low, up, mid=0, accuracy;    //区间上下限、中点、精度
	int i=0;

	cout << "请输入区间上、下限：";
	cin >> low;
	cin >> up;
	cout << "请输入精度：";
	cin >> accuracy;

	cout << endl;

	do
	

		//区间取半
		mid = (low + up) / 2;
		
		//判断根的位置
		if ((function(low) * function(mid)) < 0)    //根在前半区间
		   
			up = mid;   //将区间中点值赋值给区间上限
			i++;    //折半查找次数自增1
			cout << "第" << i << "次折半！" << endl ;
			cout << "根位于前半区间！" << endl<<endl;
		
		else   //根在后半区间
		   
			low = mid;   //将区间中点的值赋值给区间下限
			i++;   //折半查找次数自增1
			cout << "第" << i << "次折半！" << endl ;
			cout << "根位于后半区间！" << endl << endl;
		
	 while ((up - low) > accuracy);   //若i次二分区间后，区间长度小于精确度，则二分结束，找到近似根

	cout << "解为：";  //用区间中点的值作为根的近似解
	cout << mid << endl;

	return 0;