数值分析实验之非线性方程求根（MATLAB实现）

Posted 2021-02-18 ynly

一、实验目的

  1． 了解一般非线性方程的求根是比较复杂的事情：要讨论（或知道）它有无实根，有多少实根；知道求近似根常用的几种方法，每种方法的特点是什么。

  2． 用通过二分法（区间半分法）、不动点(也Picard)迭代法及Newton迭代（切线）法求其它非线性方程的根，并尽可能估计误差。

二、实验原理

    

 

 三、实验程序

    

 

 四、实验内容

   1. 用二分法求方程x³-3x-1=0在的所有根.要求每个根的误差小于0.001.

   提示与要求: (1) 利用精度找到迭代次数;

           (2) 由f(x)=3(x²-1)可取隔根区间[-2,-1].[-1,1].[1,2]);

           (3) 用程序求各隔根区间内的根.

 2. 用不动点迭代求: (1)x³+2x²+10x-20=0的所有根.

           或: (2)9x²-sinx-1=0在[0,1]上的一个根.

 3. 用Newton迭代法求解下列之一,准确到10^-5:

   (1) x³-x-1=0的所有根;

   (2) e^x+2^-x+2cosx-6=0位于[0,2]上的根.

 

 五、实验程序

    • 二分法：

文件代码：
function y = f(x)
y=x^3-3*x-1;
end

程序代码：
function Bipart(a0,b0,tol)
%a0为左区间，b0为右区间，tol为区间误差限
a=a0;b=b0;
m=ceil(log((b-a)/tol)/log(2));
for k=1:m
    p=(a+b)/2;
    if f(p)*f(b)<0
        a=p;
    else
        b=p;
    end
end
disp([‘经过二分法求得的跟为：x=‘,num2str((a+b)/2,‘%.6f‘)])
disp([‘共经过‘,num2str(k),‘次计算‘])

命令窗口：
Bipart(-2,-1, 0.001)
Bipart(-1, 1, 0.001)
Bipart (1,2, 0.001)

　运行结果：

     

 

    • 不动点法：

文件代为：
function y = f(x)
y=9*x^2-sin(x)-1;
end

程序代码：
function Budongdian(x0,tol,m)
%x0为初始值，tol为误差容限，m为最大迭代次数
syms x
F(x)=sqrt(sin(x)+1)/3;
m=m;
text=‘‘;
x=[];
x(1)=x0;
for k=1:m
   x(k+1)=F(x(k));
   if (abs(x(k+1)-x(k))<=tol)==1
       text=‘迭代成功‘;
       disp(text);
       disp([‘经过不动点迭代法求得的跟为：x=‘,num2str(x(k+1),‘%.7f‘)]);
       disp([‘共经过‘,num2str(k),‘次计算‘])
       break
   end
end
if isempty(text)==1
    disp(‘Method failed‘)
end

命令窗口：
Budongdian(1, 0.00001, 100)

　  运行结果：

  

 

    • 牛顿迭代法：

文件代码：
function y = f(x)
y=exp(x)+2^(-x)+2*cos(x)-6;
end

程序代码：
function Newton_gen(x0,tol,m)
%x0为初始值，tol为误差容限，m为最大迭代次数
syms x
F(x)=x-f(x)/diff(f(x));
m=m;
text=‘‘;
x=[];
x(1)=x0;
for k=1:m
   x(k+1)=F(x(k));
   if (abs(x(k+1)-x(k))<=tol)==1
       text=‘迭代成功‘;
       disp(text);
       disp([‘经过Newton迭代法求得的跟为：x=‘,num2str(x(k+1),‘%.7f‘)]);
       disp([‘共经过‘,num2str(k),‘次计算‘])
       break
   end
end
if isempty(text)==1
    disp(‘Method failed‘)
end

命令窗口：
Newton_ .gen(2, 0.00001, 100)

  运行结果：

   

另解：

 • 二分法：

定义函数：
function Bipart_2(a0,b0,tol,Tol)
%a0为左区间，b0为右区间，tol为区间误差限，Tol为f误差限
a=a0;b=b0;
m=ceil(log((b-a)/tol)/log(2));
for k=1:m
    p=(a+b)/2;
    if f(p)*f(b)<0
        a=p;
    else
        b=p;
    end
    if abs(f((a+b)/2))<Tol
        break;
    end
end
disp([‘经过二分法求得的跟为：x=‘,num2str((a+b)/2,‘%.6f‘)])
disp([‘共经过‘,num2str(k),‘次计算‘])
    
命令窗口：
Bipart. .2(-1, 1,0.001,0.1)
Bipart_ .2(-1, 1, 0.001, 0.000001)

  运行结果:

   

 

• 不动点法：

定义函数：
function [x,k]=budong(fun,x0,tol,m)
for k=1:m
    x=fun(x0);
    if abs(x-x0)<tol
 break;
end
x0=x;
end
x=vpa(x,8);

function t=fun(x1)
syms x;
f=9*x.*x-sin(x)-1;
s=subs(diff(f,x),x,x1);
x=x1;
f=9*x.*x-sin(x)-1;
t=x-f/s;

命令行窗口输入：
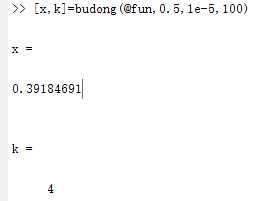
[x,k]=budong(@fun,0.5,1e-5,100)

　运行结果：