博弈论笔记：谈判与讨价还价

Posted 2022-01-05 UQI-LIUWJ

1 导言

参与其中的双方有共同利益，也有利益冲突。

讨价还价可以达成不同的协议，产生不同的利益分配，使得各方得到的好处各异（类似于多重均衡问题）。

讨价还价达不成协议的原因：可能达成的协议太多了，每一方都希望达成对自己有益的协议，结果反而任何协议都无法达成。

讨价还价问题中，如果达不成协议，那么所有人都会损失；如果达成协议，那么各方面都会得到好处，各方收益之和大于零——>讨价还价问题是具有利益冲突的正和博弈。

2 合作博弈与非合作博弈

 

2.1 合作博弈

-谈判各方联合做决策

-强调集体理性

-集体利益的最大化

-各方会合作

2.2 非合作博弈

-参与谈判的每一方独立做出决策

-强调个体理性

-个人利益最大化

-即使能够达成一个让各方利润最大化的协议，如果这个协议不是纳什均衡，那么这个协议也不会被执行

3 谈判砝码

3.1 威胁点与总剩余

威胁点（谈判砝码，非合作状态）——如果谈判破裂了（双方回到不合作状态），每一方可以得到的利益

总剩余——合作后的收益减去双方威胁点的值之和（双方合作的边际剩余增加值，就是V-a-b）

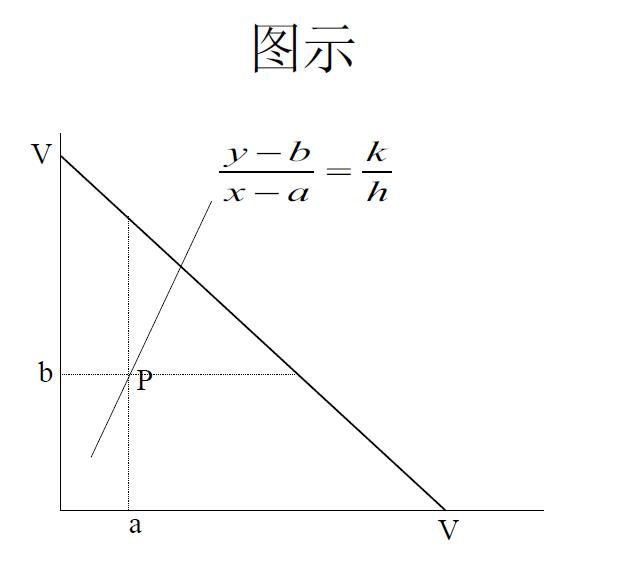
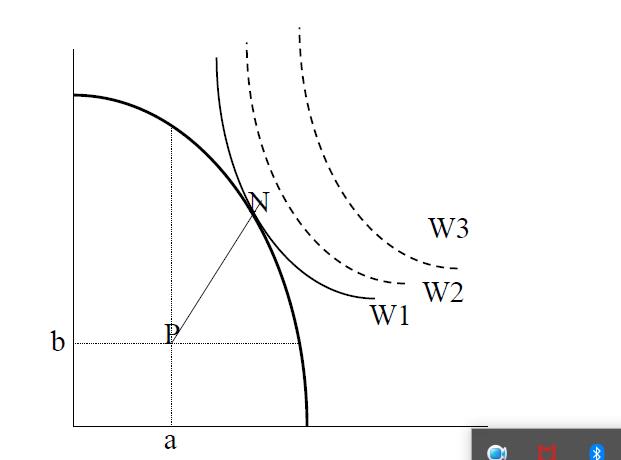
以上图为例，设想两个人，A和B，之间要就总价值等于V的分配问题讨价还价。（V——合作后的总收益，任何一种分配模式不会超过这一条斜向下的直线）

如果他们之间能达成协议，V按照协议规定分配；如果不能达成协议，A得到a，B得到b。（P（a，b)——威胁点，如果谈判结果在P的左边或者P的下边，那么这个谈判结果是绝对不可能出现的）

(a,b) 被称“威胁点”或非合作状态（status quo),是不能达成协议时的最好选择。

 a+b<V; S=V-a-b是合作带来的剩余 (surplus)。

我们用x表示A得到的价值，y表示B得到 的价值，假定A和B分别从剩余价值S中得到h和k的份额，那么：

• x=a+h（V-a-b）；x-a=h（V-a-b）

• y=b+k（V-a-b）；y-b=k（V-a-b）

于是有 (y-b)/(x-a)=k/h。

3.2 现实中可能的总价值

一般来说，总价值V并不是一个固定数，可能与分配方案有关；

在存在激励问题和边际效用递减的时候尤其如此：

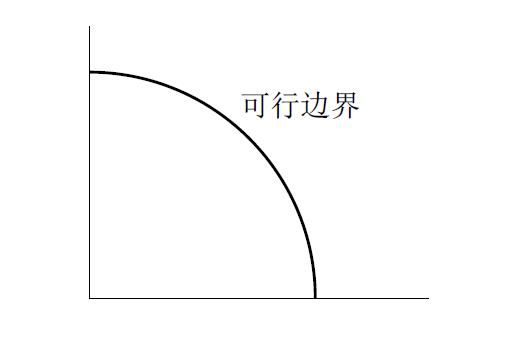
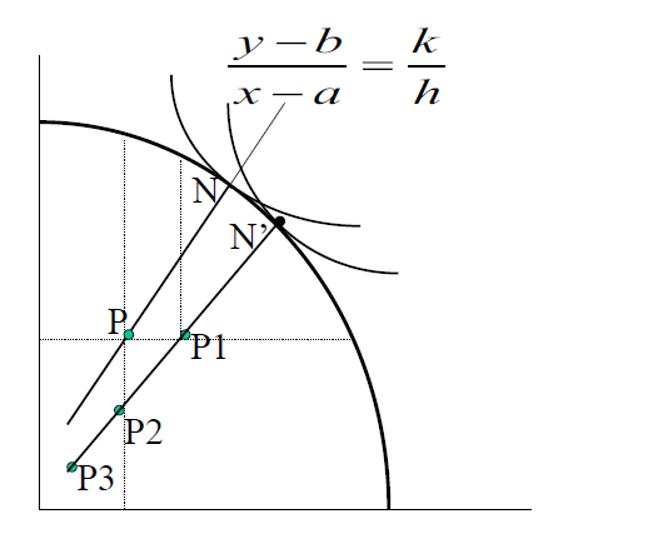
3.3 在谈判前改变谈判砝码

决定结果的是谈判砝码的相对值，而不是绝对值

4 纳什谈判解

4.1 公理化条件

纳什谈判解必须基于以下公理化条件：

1，帕累托有效——最后达成的协议应该是帕累托最优的（也就是说，不应该有没有被分配的剩 余。）

2，线性转换不变性——期望效用函数的改变不会改变个人风险决策

3，无关选择的独立性——如果原来可行的谈判结果没有被选择，去掉这些“无关”的谈判选择并不会影响讨价还价的结果

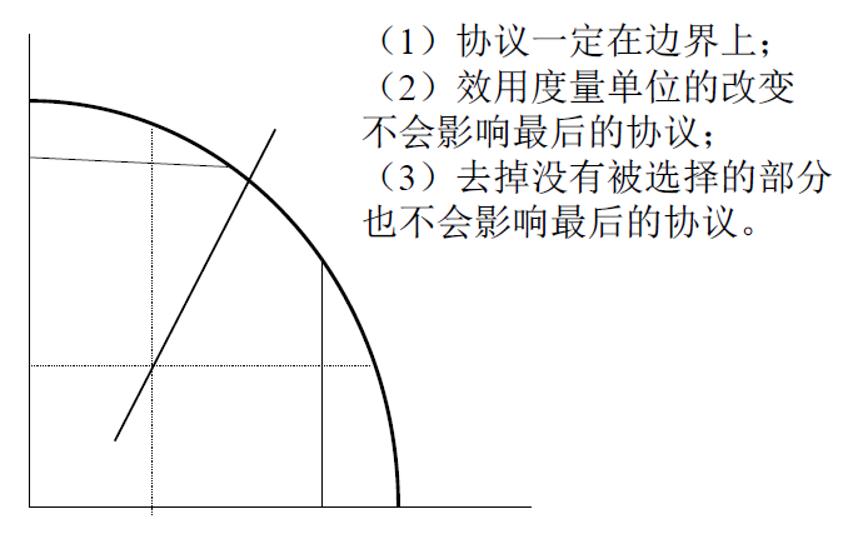
如果参与者都认可上述的公理性假设，那么双方讨价还价等价于：

满足可行性分配约束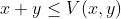的前提下，最大化纳什福利目标函数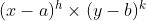

（其中，a、b是威胁点；h，k是两个参与者分到的总剩余的份额（h+k=1)），于是有：

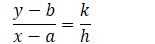
4.2 纳什福利函数的解释

（a，b）对最后的分配具有决定性的意义，可以理解为“谈判砝码”(bargaining power)。

h和k：是剩余价值的分配比例，又可以理解为谈判力（bargaining strength),可能与个人的耐心有关，或与个人的边际贡献（可替代性）有关。

如果两个人是对称的（即可分配价值以过（a，b）点的45度线对称），h=k=1/2。

5 边际贡献

边际贡献——某个参与者参与合作与不参与合作之前产生的差（这一方加入和不加入对总剩余的影响）

边际贡献率——某一个参与者的边际贡献在总的边际贡献里面所占的比例

 

当两个人的边际贡献（谈判能力）相等时，合作带来的剩余就应该平均分配。

 

 

谈判中一方得到的剩余的多少取决于它的边际贡献

产品的可替代性越高，谈判能力越低（分到的剩余越少）

产品的可替代性越低，谈判能力越高（分到的剩余越多）

提高自己的边际贡献就需要提升讨价还价能力，一种做法是合作（连锁店&单个的店；工会&单个的工人）

6 轮流出价和耐心

这时候是非合作博弈（个人利益最大化）

 

无论有限次还是无限次，影响到最终分配的是：

1，出价顺序

2，竞拍人的耐心

3，谈判成本

eg，汽车剐蹭，处理赔偿的时候如果是私了（且你全责的时候）

-如果你有耐心对方没有，那么你只要赔偿一点点

-如果你没有耐心对方有，那么你需要赔偿很多

6.1 有限次谈判

存在无穷多纳什均衡，但只有一个精炼纳什均衡

6.1.1 贴现因子和贴现率

记贴现率为s，则贴现因子为1/(1+s)

——刻画耐心程度（m∈[0,1]），这一轮的m等于下一轮的1

——m越大，耐心越大；m越小，耐心越小

6.1.2 后动优势

有限次谈判中，如果两个人的耐心足够高——谈判具有“后动优势”（谁最后一个出价，谁的优势大）。

对于最后一次谈判来说，主动提出的人肯定是想全部占有（如果接收方的效用函数是自己获得的东西的数量），那么被动接受方无论是接受还是不接受，都是效用为0，这就达到了一个均衡（均衡状态——被动接受方的效用为0）。

有限次谈判的计算方式——从最后一次的（0,1）/（1,0）逆向往前推。

 

如果只有一次谈判：逆向归纳意味着精炼纳什均衡是：x=1，y=0（x是主动提出谈判的人，y是被动接受的人）

• 如果允许谈判两次：精炼纳什均衡是：x=1-b， y=b；如果贴现率不很大，就有后动优势；（最后一轮【第二轮】，y主动提出谈判，那么这轮y希望自己全部占有【因为此时不管x接不接受，他的效用 都为0】，那么最后一轮的均衡为(0,1)；y的贴现因子是b，也就是y第一轮的b相当于第二轮的1，所以最后一轮y收益为1，倒退回来就是第一轮y收益为b，此时x收益为1-b。所以精炼纳什均衡为(1-b,b)）

• 如果谈判三次，精炼纳什均衡是： x=1-b(1-a), y=b(1-a);【第三轮：(1,0)；第二轮：(a,1-a)；第一轮：(1-b(1-a),b(1-a))】

• 如果谈判四次，精炼纳什均衡是：  x=1-b(1-a(1-b)), y=b(1-a(1-b))【第四轮:(0,1)；第三轮：(1-b,b); 第二轮：(a(1-b),1-a(1-b))；第一轮：(1-b(1-a(1-b),b(1-a(1-b))

如果两人的贴现率都不是很高（贴现因子大），也就是对未来有足够的耐心，谈判有“后动优势”(last-mover advantage)（在奇数次谈判，先动和后动是一个人）;但这个优势随允许谈判次数的增加而递减；

	最后一轮提出谈判者（奇数轮x，偶数轮y）	最后一轮接受谈判者（奇数轮y偶数轮x）
谈判一次	1	0
谈判两次	b	1-b
谈判三次	1-b(1-a)	b(1-a)
谈判四次	b(1-a(1-b))	1-b(1-a(1-b))

• 无论如何，一个人对未来越没有耐心，得到的份额越少：

6.2 无限次谈判

因为无限次谈判没有最后一次，所以我们不能用逆向归纳法求解，但可以使用和有限次谈判类似的思路得到均衡解（x，y）——计算 第T次的（x,1-x)往前推，且均衡状态下第T次状态等于第T-2次的状态。

6.2.1 先动优势

令A,B的贴现因子分别为a,b

假定在时间t>3时，A出价，得到x；

时间t-1时，B出价，给A为ax就可以了,B得到y=1-ax；

时间t-2时，A出价，给B为b(1-ax)就可以了，自己得到x=1-b(1-ax)

然后t和t-2时，A得到的是一样多的。写一个等式，于是就得到了：

无限次谈判具有“先动优势”(first-mover advantage);

• 一个人的耐心越大（贴现因子越大，贴现率越小），谈判中的优势就越大。

6.3 考虑固定谈判成本

谈判的另一类成本是固定成本，如劳资谈判拖延的话，企业可能要为客户支付违约金。

• 这类似于蛋糕随时间而变小。

 

设想蛋糕以每次1/4的量缩小，到第5期时，蛋糕已没有任何价值，第4期等于0.25, 第3期是0.50, 第2期是0.75, 第1期是1。

·那么，在第4期，B出价，将把整个蛋糕留给自己（价值=0.25);

·在第3期，A出价，自己可以得到一半的蛋糕（价值=0.25)；

·在第2期，B出价，自己可以得到2/3（价值=0.5)；

·第1期，A出价，可以得到一半（价值=0.5)。

·精炼纳什均衡: 每人1/2

 

一般情形：假定初始价值V蛋糕以x1,x2,x3,x4,x5,x6,x7,x8,x9,x10 的速度变为零。

• 精炼纳什均衡为：

– A得到 x1+x3+x5+x7+x9

– B得到 x2+x4+x6+x7+x10

7 现实中的谈判

现实中，谈判总要进行多个回合，如中国加入WTO时候的谈判，进行了好多年。

原因是：我们前面假定当事人具有完全信息：知道价值V和每个人的机会成本或谈判砝码， 每个人的耐心，谈判的时限等等。并且，每个人知道每个人知道；每个人知道每个人知道每个人知道，如此等等。

但在现实中，谈判面临的最大问题是信息不完全。  价值V，生产成本，谈判砝码（a，b），耐心， 机会成本等，双方都不一定完全知道。

谈判的过程实际上是信息揭示和窥探的过程。由于信息不对称，谈判的结果并不总是帕累托最优的；事实上，许多帕累托改进没有被利用。