博弈论笔记1：囚徒困境与纳什均衡

Posted 2021-07-16 刘文巾

1 个体最优与社会最优

1.1 社会基本问题

社会：个体之间有互动行为&相互依赖的群体

羊群效应：大家做什么，我就跟着做什么，不管对错和原因

 

协调问题：两人迎面走来，谁左谁右？（核心：人们如何预测他人的行为）

合作问题：囚徒困境（核心：个体理性和集体理性的折衷）

等边际原理：如果每一种资源都存在着边际收益递减，那么最优的资源配置策略应该满足：最后一单位资源无论用在哪一种用途上，都会产生相同的收益。 【资源在每一种用途上的边际贡献相等】

1.2 个体理性行为

理性人：有一个明确的偏好+在给定约束条件下，这个人总是追求自我偏好最大化。

 

输赢的不对称：当人们面临风险决策时， 他们更在乎的是成功与失败，赢和输， 财富的变化，而不是最终的财富状态；（比如说，100元损失导致的效用的减少远远大于100收益导致的效用的增加）——>人们是损失规避型的(loss aversion)；

1.3 社会最优

1.3.1 帕累托效率标准：

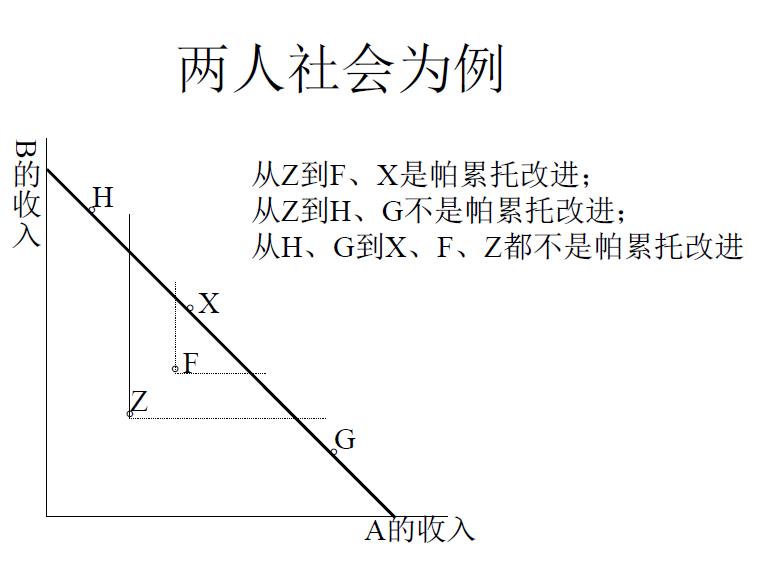
帕累托效率：一种社会状态，与该状态相比，不存在任何一种可选择的状态，使得至少一个人的状态更好，同时没有任意一个人的状态变差

帕累托改进：改变一种状态，使得没有任何一个人的处境变坏，但是至少有一个人的处境变好了

**从非帕累托最优点到帕累托最优点不一定是帕累托改进

1.3.2 卡尔多-希克斯标准

总量最大化

2 囚徒困境

2.1 占优策略

不管对方使用什么样的战略，只要参与人使用这一战略，都可以给自己带来最大的收益。

理性人做决策的时候，不需要假定对方是理性的。

占优战略均衡：由占优战略组成的战略组合。

2.2 囚徒困境

尽管合作能让双方更好，但双方仍然不会合作

怎么比较好地去记一个方框里面哪个是甲的收益哪个是乙的收益呢？我们画一条线，斜线上方的就是表格“上方”的乙的收益；斜线左边的就是表格“左边”的甲的收益。

两个假设：

       R>T>P>S

       T+T>R+S

只要满足这两个条件，一定是个人理性选择不满足集体理性选择。

在这两个假设下，集体理性肯定是选择（合作，合作），这样总体的利益最高。

但是个人理性观点下呢？

以甲为例，当乙合作的时候，我们看下图蓝框框住的部分。如果甲合作，那么甲收益为T；甲不合作，甲的收益为R，又R>T，所以乙合作的时候，甲会不合作；同理，乙不合作的时候，甲也不合作（P＞S）。所以无论乙怎么选择，甲都不合作。

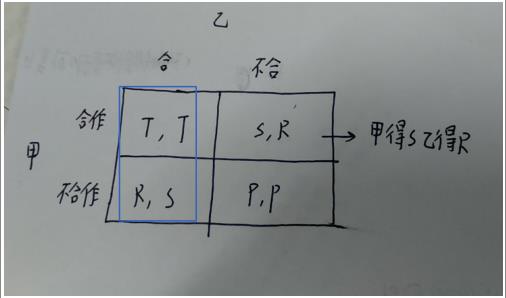
乙同理，不论甲怎么选择，乙的占优策略都是不合作

2.2.1 囚徒困境的解决方法

设立奖惩机制，适当地减少R，增大S

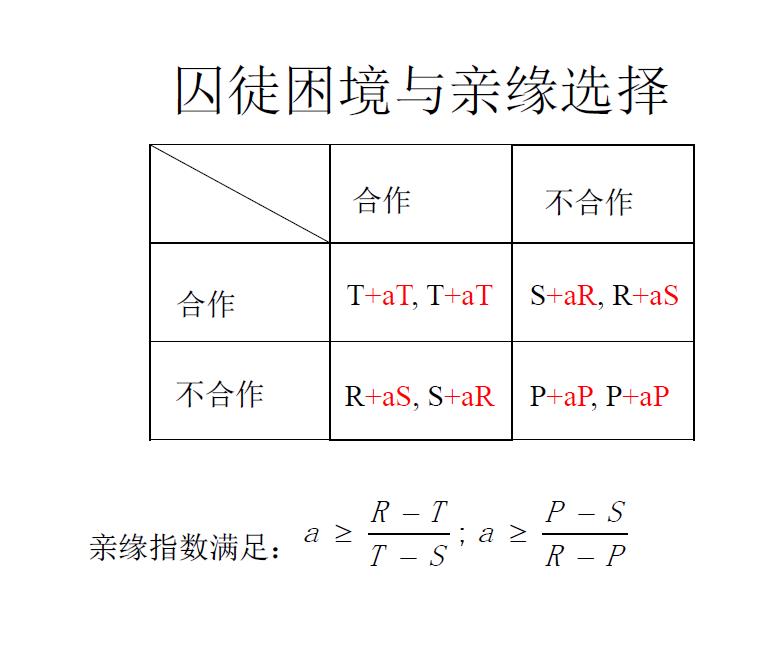
如果需要二者合作，那么T+aT≥R+aS，S+aR≥P+aP

3 智猪博弈

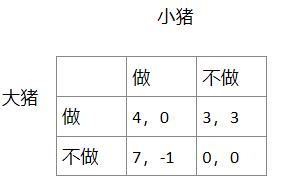
我们先考虑小猪：

如果大猪做，那么小猪不做；如果大猪不做，那么小猪也不做——>小猪的占优策略是不做

我们考虑大猪：

如果小猪做，那么大猪不做；如果小猪不做，那么大猪做——>大猪没有占优策略。

但如果大猪事先知道小猪是理性的，那么大猪就会知道小猪不做，所以对于大猪来说，只剩下一半的博弈矩阵，那么大猪选择做就可以了。

所以最后的均衡状态是（做，不做）

4 纳什均衡

纳什均衡：所有参与人的最优战略的组合，给定这一组合中其他参与人的选择，没有任何人有积极性改变自己的选择。

 

混合战略纳什均衡：均衡结果是参与人以某一概率随机选择行动。

纯战略纳什均衡：参与人确定的选择某一个特定的战略【退化混合战略纳什均衡】。

4.1 监督博弈

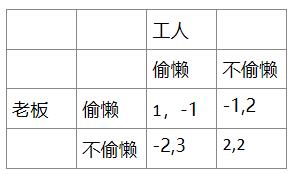
假如一开始是（偷懒，偷懒）

->如果老板偷懒，那么工人不偷懒

->如果工人不偷懒，那么老板不偷懒

->如果老板不偷懒，那么工人偷懒

->如果工人偷懒，那么老板偷懒

这样又循环回去了，也就是说，这里没有纯战略的纳什均衡。

 

假如老板认为员工偷懒的概率是P，不偷懒的概率是1-P。

从老板的角度，自己不偷懒的期望收益是-2*P+2*(1-P)=2-4P，偷懒的期望收益是1*P+-1*（1-P)=2P-1

从员工的角度，自己不希望老板猜到自己偷懒还是不偷懒：

2-4P=2P-1 ->  P=1/2

这时，员工1/2的概率偷懒，1/2的概率不偷懒

 

假如老板以Q的概率偷懒，1-Q的概率不偷懒

从员工的角度，自己偷懒的期望收益是-1*Q+3*（1-Q)=3-4Q

自己不偷懒的期望收益是2*Q+2&（1-Q）=2

还是两者应该相等

所以Q=1/4

也就是老板以1/4的概率偷懒，3/4的概率不偷懒

 

所以，这个博弈的纳什均衡是，员工1/2的概率偷懒，1/2的概率不偷懒;老板1/4的概率偷懒，3/4的概率不偷懒。

4.2 纳什均衡的存在性

每一个有限博弈至少存在一个纳什均衡（纯战略或混合战略）；

• 如果一个博弈存在两个纯战略纳什均衡，那么，一定存在第三个混合战略纳什均衡。如果有偶数个纯纳什均衡，那么必然至少存在一个混合纳什均衡）