博弈论笔记：不完全信息与声誉

Posted 2021-07-16 刘文巾

1 连锁店悖论

我们看以下的情况

假设市场上一共有20个在位者。

如果这20个在位者互相没有关系：

        我们用逆向思维考虑精炼纳什均衡。

        当一个进入者要进入的时候，单个在位者会选择默许。

        然后在在位者选择默许的情况下，进入者会选择进入。

        ——》于是最后的均衡情况为，进入者进入，20个在位者默许

如果20个在位者组成了连锁店：

        那么当进入者准备进入第一个市场的时候，在位者争斗，使得进入者之后都不敢进入。

        这样虽然短期会赔本，但长期来看，赚的更多

2 多重均衡下的惩罚与合作

我们看一下这样的博弈：

2.1，单次博弈

        有两个纳什均衡（L，L）,（R，R）；该博弈的帕累托最优为（M，M）

2.2，两次博弈-策略1

        那么进行到第二次博弈的时候，由于博弈到此结束，所以双方肯定是选择纳什均衡中的一个。

       如果双方采取这样的策略：如果第一次自己选择M，且对方也选择M，那么双方会在第二次博弈中选择R；否则的话，双方第二次博弈中将选择L。那么这样双方第一回合会不会合作呢？

        我们把两次博弈的收益合并成一张表： 

	L	M	R
L	2,2	6,1	1,1
M	1,6	7,7	1,1
R	1,1	1,1	4,4

        表中只有M,M加的是3,3；别的加的都是1,1

        此时有三个纳什均衡，（L,L),(M,M),(R,R)。

        奖惩能力主要体现在第二次博弈时，参与人可以在两个报酬不等的纳什均衡中进行选择。

        但是，由于（3,3）大于（1,1），理性的人在第二轮不会选择（1，1）代替（3，3）来进行惩罚，因为这样有损自己的利益——>这就导致了惩罚不可信。所以这是纳什均衡，但不是精炼纳什均衡。

2.3 两次博弈-策略2

        我们对上面的策略改进一下：

        使得我们单次的收益如下：

此时的策略为：

如果第一次博弈甲（乙）不合作，那么第二阶段乙（甲）选择Q（P）

如果第一阶段甲乙合作，那么第二阶段两者选择R,R

那么这时候威胁可信。第一次双方选择合作就是精炼纳什均衡了。

3 不完全信息

3.1 KMRW模型

        如果参与人对其他参与人的效用函数和 战略空间的信息不完全，即使博弈重复的次数是有限的，人们也有积极性建立一个合作的声誉(reputation)。即合作会出现。

3.2 单方面不完全信息

假定有两个参与人， A 和 B ，进行囚徒困 境博弈。如下图。

• 参与人 A 有两中可能的类型：

        1，“非理性” 型：只有一种战略，tit-for-tat (针锋相对，TFT)，概率为p;

        2，“理性”型：可 以选择任何战略，概率为（1-p ）；

• 参与人 B 有一种类型：理性型。

3.2.1 博弈重复两次

当博弈进行到第二次的时候，理性的B必定会选择“背叛”以最大化自己的收益

如果A是理性的，那么A第二次会选择背叛

如果A是非理性的，那么A第二次的选择会取决于B第一次的选择

如果A是理性的，那么他在第一次也一定会选择背叛（因为无论A选择哪个，B第二次一定是背叛）

如果A是非理性的，那么他第一次一定会本能地选择合作

但B的第一次则无法确定。因为他不清楚A是不是理性的，如果一开始背叛的话，会有一定概率失去第二次赚更多的可能性。

所以我们重点看一下B第一次的选择：

1）如果B第一次选择背叛：

第一阶段：

A有p的概率合作，此时B获利4*p

A有1-p的概率不合作，此时B获利0*（1-p）

综合来说，B第一阶段获利4P

第二阶段：

A无论理性不理性，都会背叛，所以B获利0

总之，如果B选择背叛，其两阶段总获利为4P

2）如果B第一次选择合作

第一阶段：

A有p的概率合作，此时B获利3*p

A有（1-p)的概率不合作，此时B获利-1*（1-p）=-1+p

第二阶段

A有p的概率合作，此时B获利4*p （非理性会继续合作）

A有1-p的概率不合作，此时B获利0

总之，如果B选择合作，其两阶段获利为8p-1

如果8p-1≥4p，即p≥0.25，那么B会选择合作

3.2.2 博弈重复三次

如果A是理性的，那么他在第一阶段就不合作不一定是最好的选择（因为如果自己第一阶段就背叛，那么立马暴露了自己理性的特点，那么B在第二阶段也会选择背叛）

但如果A是理性的，倒数第二阶段和最后一个阶段肯定是背叛。（因为B是理性的，所以最后一个阶段一定会背叛，所以A最后一个阶段也要背叛；然后倒数第二个阶段A也不用“藏着掖着”了，选择背叛与否，也就是自己理性状态暴露与否都不会影响理性B最后一次的决策。）

——>A要抉择自己在第一轮暴露身份是否值得（因为 建立一个合作的形象可以换取B在第2阶段的合作；）

我们先看理性的A：

如果p（A非理性的概率）>=0.25, 并且A认为B在第1阶段会合作。

给定A在第1阶段合作的话B在在第2阶段也会合作，那么A选择合作得到：3+4+0=7；

如果 A 选择背叛，得到： 4+0+0=4 ；

所以如果在上述情况下，A在第一阶段合作是最优的。

我们再看B：

我们分别讨论一下：

整合一下四种情况：

结论如下：

只要 p>=0.25, 下表所列战略组合是一个 精炼纳什均衡：

– 理性型 A 在第 1 阶段选择合作，然后在第 2 和 第3 阶段选择背叛；

– B 在第 1 和第 2 阶段选择合作，然后在第 3 阶段背叛。

即下图这种情况：

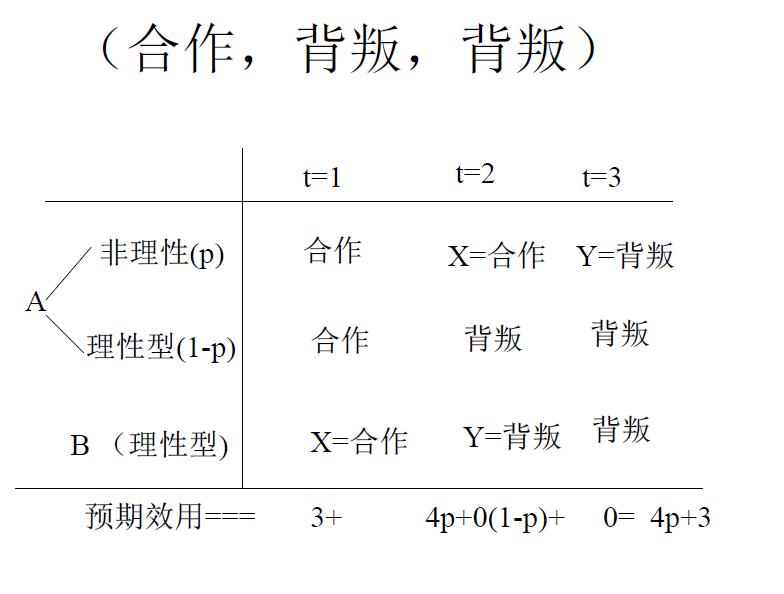
３.３　大于等于三次博弈的一般结论

对于这样一个博弈，只要A非理性的概率p≥0.25，那么对于所有的T≥3，下列战略组合构成了一个精炼纳什均衡

理想型A：在t=1,…..,T-2选择合作，在T-1和T阶段选择背叛

理想型B：在t=1,…..T-1选择合作，在T阶段选择背叛

即背叛只在最后两个阶段会出现

——信息不完全时，理性的参与人有积极性去建立一个合作型声誉

对参与人A，如果他是理性的，那么在安完全信息的情况下他是不会合作的，但是在信息不完全的情况下，他不会过早地暴露自己的理性特征，因而在倒数第二个阶段也没有必要去假装自己非理性。

对参与人B，如果一早就不合作，那即使对方是合作型也不会合作了。因此，权衡长远利益&眼前利益后，B一开始也选择合作

４　双方信息不完全

在单方不完全信息下，只要 p<0.25 ，不论博弈重复多少次，合作都不会出现。

但如果双方信息不完全，即使小小的不确定性也会导致合作行为，只要博弈重 复的次数足够多（不需要是无限次）

原因在于，如果博弈重复的次数足够长，没有任何一方愿意一开始就把自己的名 声搞坏。

４.１　双方信心不完全的例子

还是之前的博弈收益

假定非理性型选择冷酷策略（双方一开始都合作，一旦一方不合作，之后就再也不合作了）

• 如果 A 在一开始就选择背叛，暴露了自己是非合作型的，从第2 期开始的唯一的均衡是每个

人都背叛；所以 A 的最大预期收益为： 4+0+0+…=4;

• 假定选择如下战略：开始选择合作，直到对方 选择不合作，之后永远背叛。最小预期收益是：

         p(3T)+(1-p)(-1+0+0+)=p(3T)-(1-p)

如果3pT-(1-p)≥４，那么A一开始会选择合作，此时得到一个临界值T*

所以，无论 p 多小，只要博弈重复的次数 足够大，一开始就选择背叛不是最优的。

５　KMRW定理

        在不完全信息的情况下，只要博弈重复 的次数足够长，参与人就有积极性在博弈的早期建立一个“合作”的声誉；只是在博弈的后期，才会选择背叛；并且，非合作阶段的数量只与p 有关，而与博弈的次数T 无关。