12月学习进度3/31—计算机图形学期末准备01拉格朗日插值 + 三次Hermite插值
Posted fu_GAGA
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了12月学习进度3/31—计算机图形学期末准备01拉格朗日插值 + 三次Hermite插值相关的知识,希望对你有一定的参考价值。
相关概念
- 型值点:事先给定的离散点
- 插值:得到的曲线通过所有的型值点
- 逼近:不要求通过给定的所有型值点,用给定型值点控制曲线形状
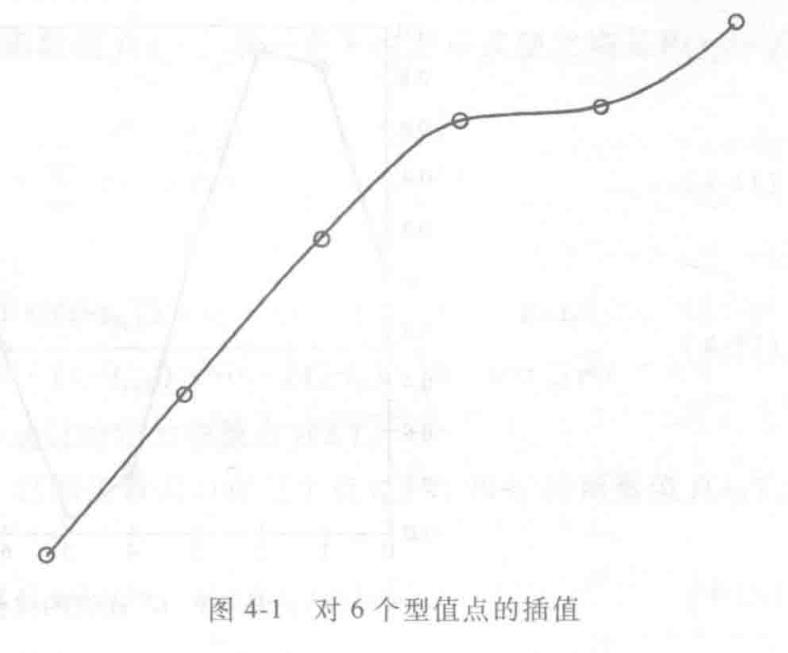
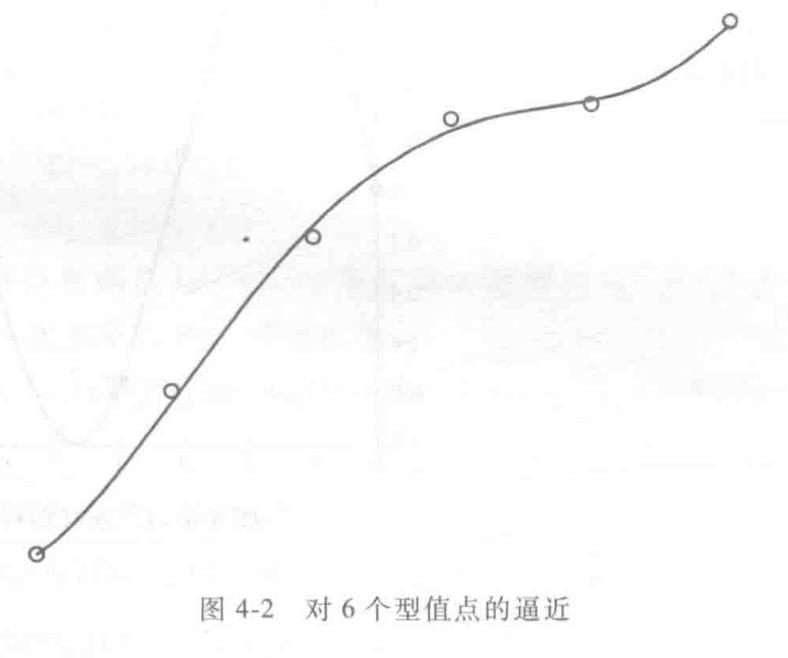
Hermite多项式

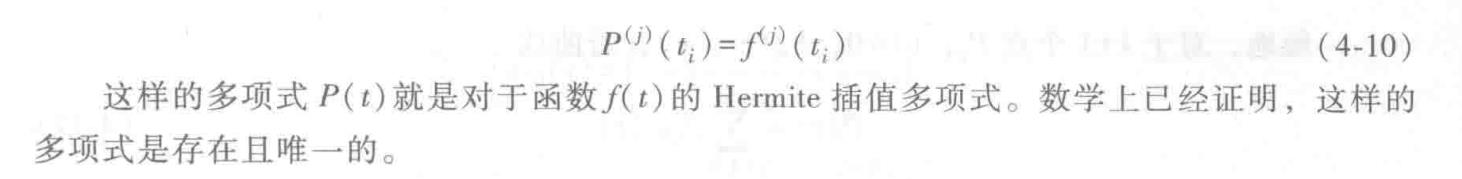
拉格朗日插值
拉格朗日插值是当
j
=
0
j=0
j=0 时,即只给出函数值的Hermite多项式插值问题。

参考通俗易懂讲解视频
拉格朗日插值多项式:
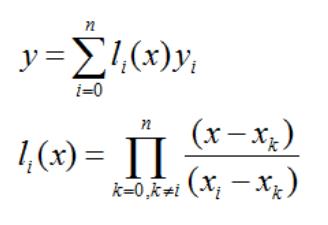
其中
l
i
(
x
)
l_i(x)
li(x) 是插值基函数,它类似开关。
因为当且仅当
x
=
x
i
x = x_i
x=xi 时,
l
i
(
x
i
)
l_i(x_i)
li(xi)为1,否则为0;
相当于
x
=
x
i
x = x_i
x=xi时,开关
i
i
i 打开,其余开关均闭合,
f
(
x
i
)
=
y
i
f(x_i) = y_i
f(xi)=yi
这就保证了 给定
n
+
1
n+1
n+1 个点,拉格朗日插值法可以构造出
n
n
n 阶多项式,恰好穿过这
n
+
1
n+1
n+1 个点
f
(
x
i
)
=
y
i
f(x_i)=y_i
f(xi)=yi
(
i
=
0
,
1
,
2
,
.
.
.
,
n
)
(i = 0,1,2,...,n)
(i=0,1,2,...,n)
Q:n+1个点为什么构造n阶插值多项式?
n阶多项式:
f
(
x
)
=
a
0
+
a
1
∗
x
+
a
2
∗
x
2
+
a
3
∗
x
3
+
.
.
.
+
a
n
∗
x
n
f(x) = a_0 + a_1*x + a_2*x^2 + a_3*x^3 + ... +a_n*x^n
f(x)=a0+a1∗x+a2∗x2+a3∗x3+...+an∗xn
n阶多项式有
n
+
1
n+1
n+1 个系数(
a
0
,
a
1
,
.
.
.
a
n
a_0,a_1,...a_n
a0,a1,...an)
n+1个点 <==> n+1个条件(方程)<=> 可解n+1个变量 <=> n阶多项式可确定

对于一组给定的点,拉格朗日插值法总能给出一条最低次数函数穿过这些点
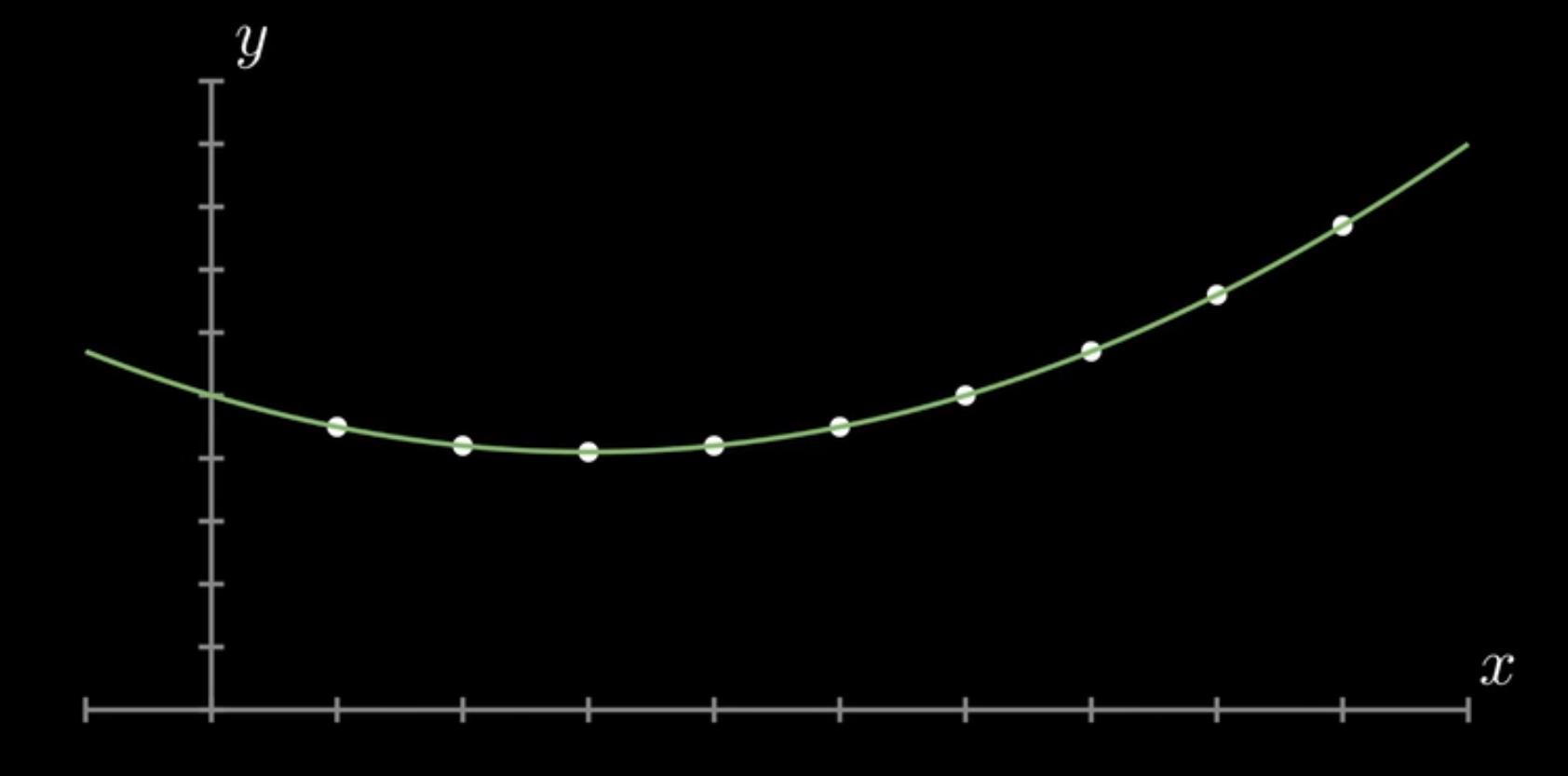
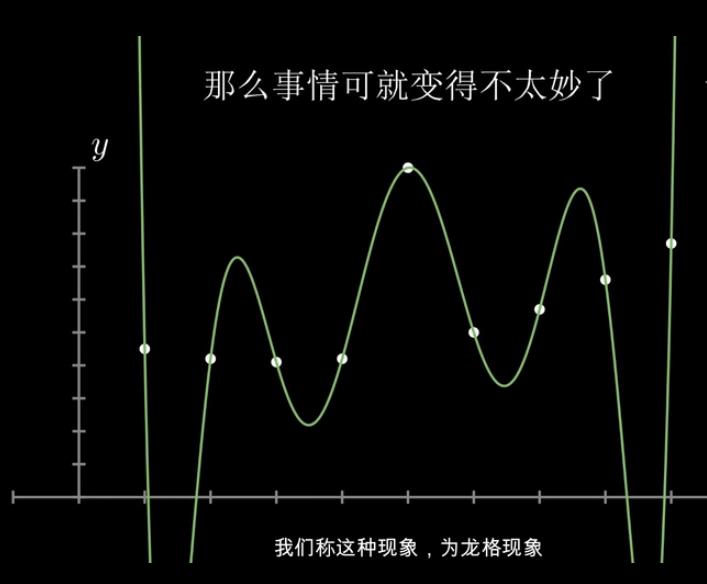
但当一组连续均匀的点中出现一个“叛徒”(异常点),则拉格朗日插值就会想办法通过这个点,则就会出现龙格现象(Runge Phenomenon)。
【龙格现象】参考视频演示
利用多项式对某一函数进行逼近时,多项式次数越高,插值结果反而越偏离原函数的现象。(次数比较高时,产生剧烈的振荡)
例题
已知函数
f
(
x
)
f(x)
f(x),
f
(
144
)
=
12
,
f
(
169
)
=
13
,
f
(
225
)
=
15
f(144)=12 , f(169)=13 , f(225)=15
f(144)=12,f(169)=13,f(225)=15.
求
f
(
x
)
f(x)
f(x) 的二次拉格朗日插值多项式.
解:
- 题目给定离散点:
(
x
0
,
y
0
)
,
(
x
1
,
y
1
)
,
(
x
2
,
y
2
)
(x_0,y_0) , (x_1,y_1) , (x_2,y_2)
(x0,y0),(x1,y1),(x2,y2)
其中 x 0 = 144 , y 0 = 12 , x 1 = 169 , y 1 = 13 , x 2 = 225 , y 2 = 15 x_0 = 144,y_0=12 , x_1=169,y_1=13,x_2= 225,y_2=15 x0=144,y0=12,x1=169,y1=13,x2=225,y2=15 ; - 构造插值基函数
l
i
(
x
)
l_i(x)
li(x)
l 0 ( x ) = ( x − x 1 ) ( x − x 2 ) / ( x 0 − x 1 ) ( x 0 − x 2 ) l_0(x) = (x-x_1)(x-x_2)/(x_0-x_1)(x_0-x_2) l0(x)=(x−x1)(x−x2)/(x0−x1)(x0−x2)
l 1 ( x ) = ( x − x 0 ) ( x − x 2 ) / ( x 1 − x 0 ) ( x 1 − x 2 ) l_1(x) = (x-x_0)(x-x_2)/(x_1-x_0)(x_1-x_2) l1(x)=(x−x0)(x−x2)/(x1−x0)(x1−x2)
l 2 ( x ) = ( x − x 0 ) ( x − x 1 ) / ( x 2 − x 0 ) ( x 2 − x 1 ) l_2(x) = (x-x_0)(x-x_1)/(x_2-x_0)(x_2-x_1) l2(x)=(x−x12月学习进度7/31——计算机图形学期末准备04B样条曲线及其基函数的定义12月学习进度8/31——计算机图形学期末准备05B样条曲线和基函数的性质
12月学习进度5/31——计算机图形学期末准备02规范化两点三次Hermite插值及MATLAB实现
12月学习进度9/31——计算机图形学期末准备06四阶三次B样条曲线矩阵形式推导及MATLAB实现