漫画：什么是“贪心算法”？如何求解“部分背包问题”？

Posted 2021-11-22 程序员小灰

—————  第二天  —————

————————————

. . . . . . . .

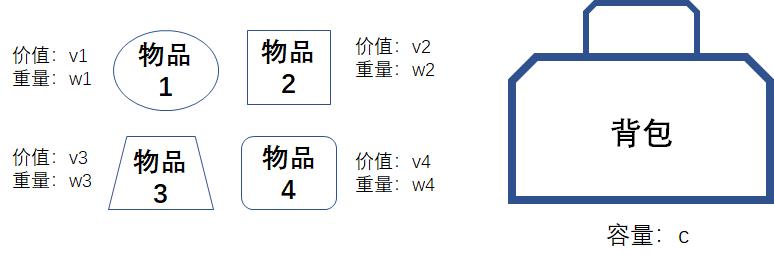
我们回到刚才的题目当中，假设背包的容量是10，有5个商品可供选择，每个商品的价值和重量如图所示：

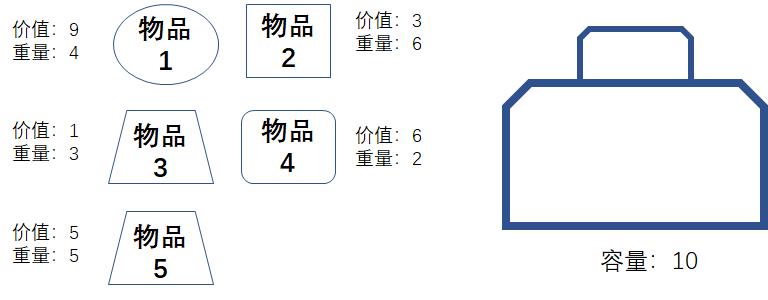
让我们来计算一下每件物品的性价比，其结果如下：

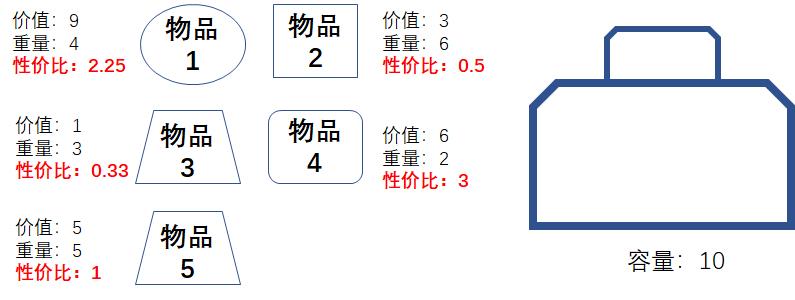
毫无疑问，此时性价比最高的是物品4，我们把物品4放入背包当中，背包剩余的容量是8：

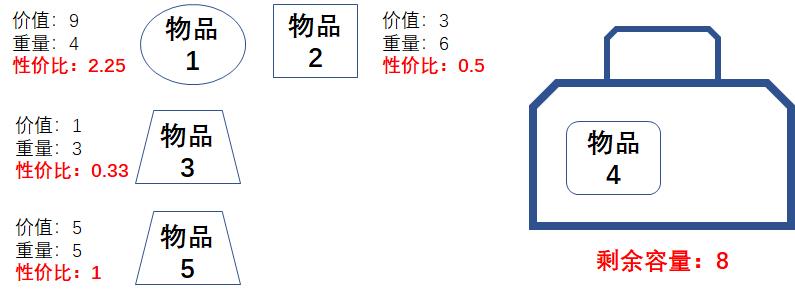
我们选择物品1放入背包，背包剩余的容量是4：

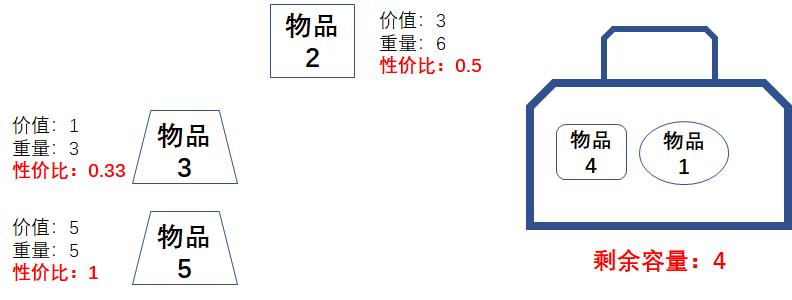
于是，我们选择0.8份的物品5放入背包，背包剩余的容量为0：

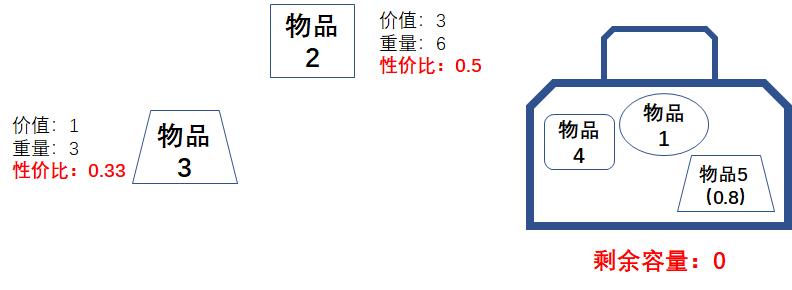
public static void main(String[] args) {
        int capacity = 10;
        int[] weights = {4,6,3,2,5};
        int[] values = {9,3,1,6,5};
        System.out.println("背包最大价值：" + getHighestValue(capacity, weights, values));
    }

    public static double getHighestValue(int capacity, int[] weights,int[] values){

        //创建物品列表并按照性价比倒序
        List<Item> itemList = new ArrayList<>();
        for(int i=0;i<weights.length;i++){
            itemList.add(new Item(weights[i], values[i]));
        }
        itemList = itemList.stream().sorted(Comparator.comparing(Item::getRatio).reversed()).collect(Collectors.toList());

        //背包剩余容量
        int restCapacity = capacity;
        //当前背包物品的最大价值
        double highestValue = 0;

        //按照性价比从高到低选择物品
        for(Item item : itemList){
            if(item.weight <= restCapacity){
                highestValue += item.value;
                restCapacity -= item.weight;
            }else{
                //背包装不下完整物品时，选择该件物品的一部分
                highestValue += (double)restCapacity/(double)item.weight * item.value;
                break;
            }
        }

        return highestValue;
    }

    static class Item {
        private int weight;
        private int value;
        //物品的性价比
        private double ratio;

        public Item (int weight, int value){
            this.weight = weight;
            this.value = value;
            this.ratio = (double)value / (double)weight;
        }

        public double getRatio() {
            return ratio;
        }
    }

在这段代码当中，我们借助了静态内部类Item，从而更方便地记录性价比、获取重量和价值信息、按性价比排序。

仍然给定一个容量是10的背包，有如下三个物品可供选择：

这一次我们有个条件限制：只允许选择整个物品，不能选择物品的一部分。

如果按照贪心算法的思路，首先选择的是性价比最高的物品1，那么背包剩余容量是4，再也装不下其他物品，而此时的总价值是6：

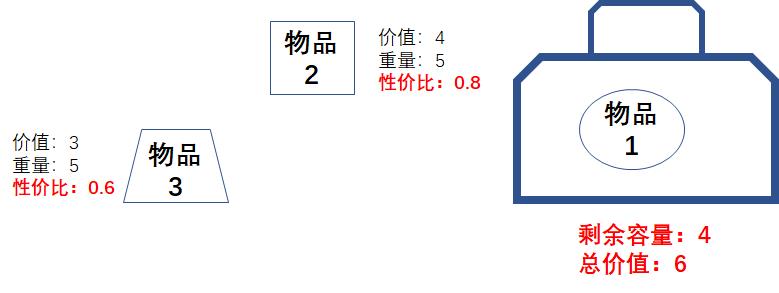
但这样的选择，真的能让总价值最大化吗？如果我们不选择物品1，选择物品2和物品3的话，剩余容量是0，总价值是7：

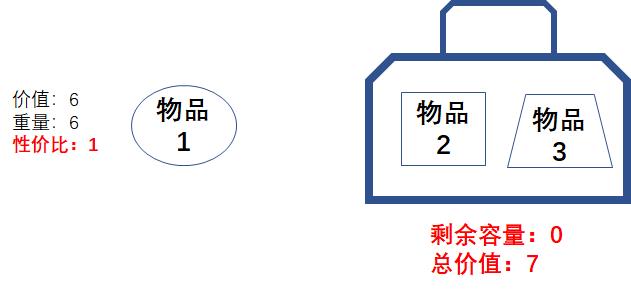
显然，7>6，依靠贪心算法得出的结果，未必是全局最优解。

漫画：什么是动态规划？（整合版）