从斐波那契到矩阵快速幂

Posted 2021-10-23 秀到没朋友

        斐波那契数列相信大家都不陌生，从第三项开始每一项都是前两项的和。

        F(N)=F(N-1)+F(N-2)(N>2);//假设不存在F(0)

        想想最初我们是怎么做的：

int fibo(int n){
    if(n<=2){
        return 1;
    }
    return fibo(n-1)+fibo(n-2);
}

        相信大家对这段代码并不陌生(递归可是困扰俺好久)

        虽然这么写很方便，但是n稍微大一点就需要很长时间，所以聪明的程序员们就想出了优化版本（利用迭代）

​
int fibo(int n){
	int a = 1, b = 1, c=0;
	if (n <= 2){
		return 1;
	}
	for (int i = 3; i <= n; i++){
		c = a + b;
		a = b;
		b = c;
	}
	return c;
}

​

        利用三个变量不断循环迭代最终得到结果（这样比递归快不少嘞）

        但是随着n继续增大，貌似迭代也不能满足人们对效率的追求，于是我们今天的主角矩阵快速幂就诞生了。

        我们先来了解一下什么是快速幂

        假如要求一个数的 n 次方，我们首先想到的思路是这样的

int pow(int num, int n){
	int res = 1;
	for (int i = 1; i <= n; i++){
		res *= num;
	}
	return res;
}

        一个为1的变量乘n次num就得到了num的n次方（只考虑正整数的话）

        但是这样就要计算n次，怎么才能计算的更快呢，我们考虑把n表示成二进制的形式

        举个例子，假如现在要计算 21 的 9 次方

        上面的方法我们要计算9次

        不妨我们把九转化成二进制 

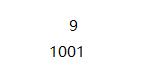
        然后让从低到高一次遍历每个位，第一个位代表 21 的 1 次方，第二个位代表 21的 2 次方，

第三个位代表21的4次方，第四个位代表21的8次方，当这个位为 1 时res*=21的某次方，为零时不管

        也就是res=1;   res*=21^1;   res*=21^8;

        res-->1-->21^1-->21^9;

        好的我们来看下代码

 

long long  q_pow(int num, int n){
	long long res = 1;
	while (n){
		if (n & 1){
			res *= num;
		}
		num *= num;
		n >>= 1;
	}
	return res;
}

！！！！（不要试21的九次方哦，long long都放不下）

这样就把O(n)的复杂度优化成了O（logN）。

        既然是矩阵快速幂，那必然是要与矩阵产生联系的（默认大家学过线性代数了哈）

        （请原谅我这残废的双手）

        

 

 

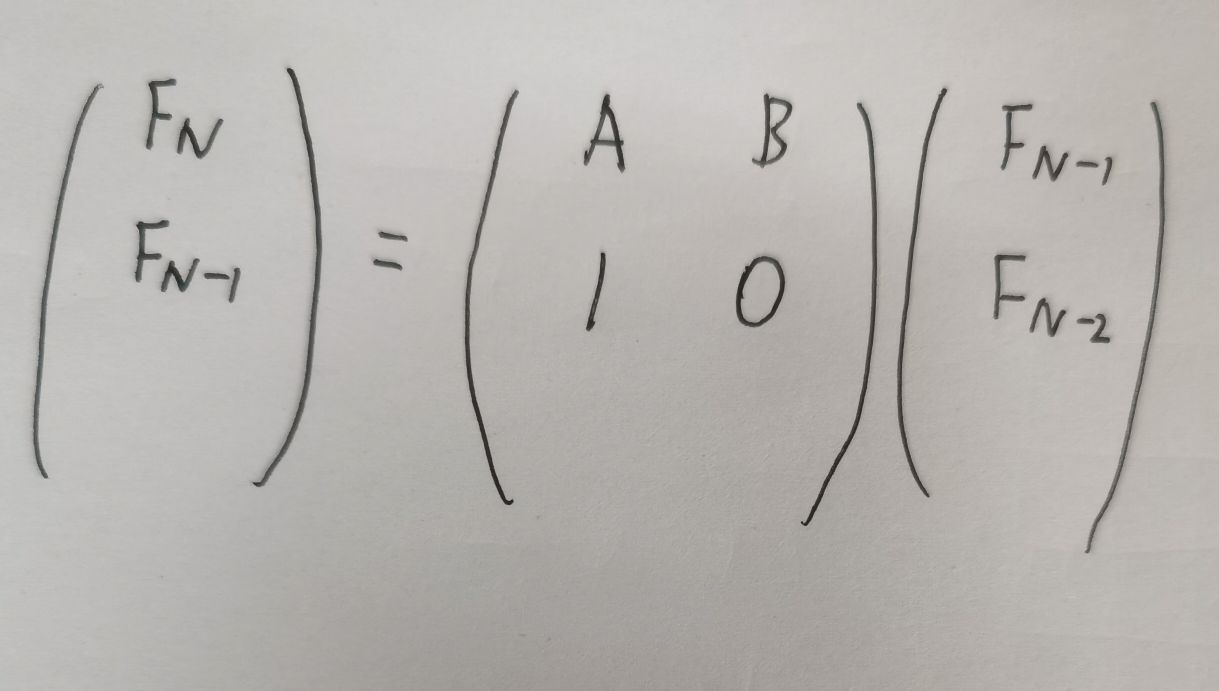
        F（N）=A*F(N-1)+B*F(N-2)

 然而F（N-1）与F（N-2）这个矩阵可以继续递推

 

 

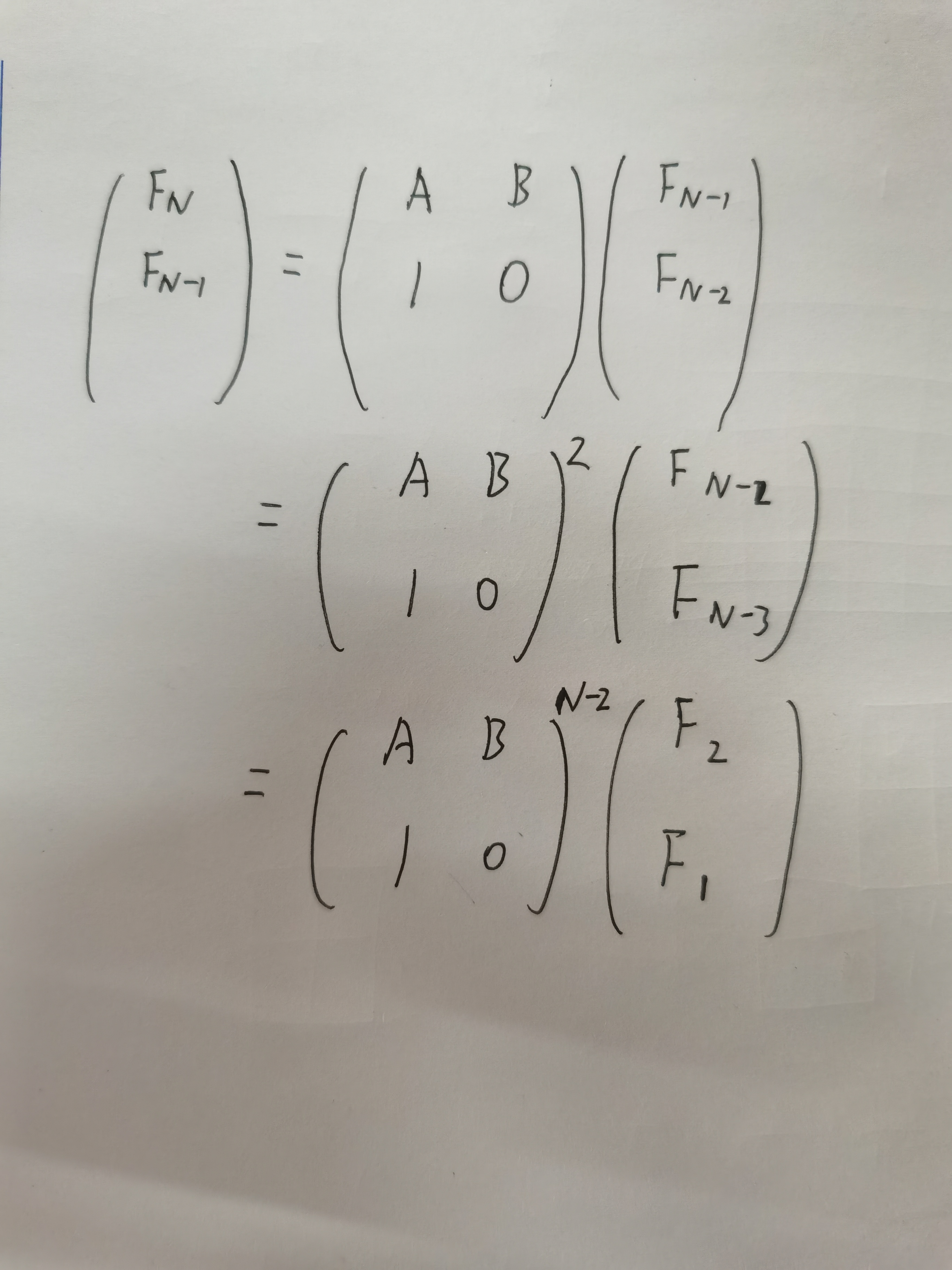
 这样的话我们就得到了两个常矩阵的乘积，A，B，F1，F2都是已知的，只要快速求出前面矩阵的N-1次幂在与后面矩阵相乘，结果矩阵的第一行第一列就是我们要的答案了。

        但是前面的常量矩阵是要自己推导的！！！一般情况下递推式有n项常矩阵n×n

 下面我们来看下具体代码怎么写

#include<iostream>

using namespace std;

typedef struct matrix{
	int arr[2][2];
	matrix operator*(matrix &B){//为方便操作重载*运算符，也可以封装函数实现
		matrix res = {0};
		for (int i = 0; i < 2; i++){
			for (int j = 0; j < 2; j++){
				for (int k = 0; k < 2; k++){
					res.arr[i][j] += arr[i][k] * B.arr[k][j];
				}
			}
		}
		return res;
	}
}matrix;
matrix q_pow(matrix A,int n){
	
	matrix tem = { 1, 0, 0, 1 };
	if (n < 0){
		return tem;
	}
	while (n){
		if (n & 1){
			tem = tem*A;
		}
		A = A*A;//!!!(不要用*=，因为我们没重载*=运算符)
		n >>= 1;
	}
	return tem;
}

int main(){
	int n;//n代表递推式多少项
	int A, B,a,b;//A，B表示递推式系数a,b 表示F1，F2
	cin >>n>> A >> B >> a >> b;
	matrix T = { A,B,1,0 };//我们推导的常矩阵
	T=q_pow(T, n-2);//T表示常矩阵的n-2次幂
	long long res = T.arr[0][0] * b + T.arr[0][1] * a;
	cout << res << endl;
	while (1);
	return 0;
}

我们可以简单测试下

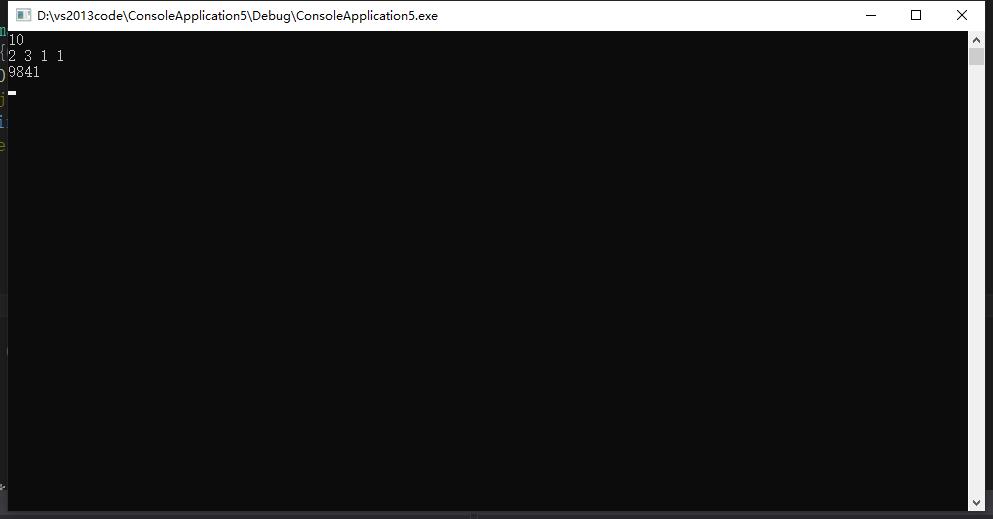
 然后写一个最简单的递归版本

 答案是ok的（过大的常数是会导致数据溢出的）