[P1962] 斐波那契数列 (矩阵快速幂)
Posted nnezgy
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了[P1962] 斐波那契数列 (矩阵快速幂)相关的知识,希望对你有一定的参考价值。
题意:求出 f(n) mod 1000000007 的值,n 在long long 范围内;
解法:矩阵快速幂;
1.矩阵快速幂;
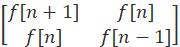 =
=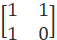 X
X 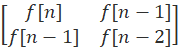 …………①
…………①
同理:
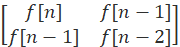 =
= 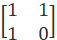 X
X 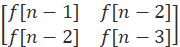 …………②
…………②
我们把②式带入①式
得:
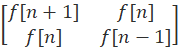 =
= 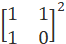 X
X 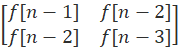
附上代码:
#include<cstdio> #include<cstring> #include<iostream> #include<algorithm> #define ll long long #define rg register using namespace std; const int mod = 1e9+7; ll n; ll a[101][101],b[101][101]; ll ans[101][101]; inline void matrix(){ memcpy(b,ans,sizeof(ans)); memset(ans,0,sizeof(ans)); for(rg int k=1;k<=2;++k) for(rg int i=1;i<=2;++i) for(rg int j=1;j<=2;++j) ans[i][j]=(ans[i][j]+(b[i][k]*a[k][j])%mod)%mod; } inline void matrix_(){ memset(b,0,sizeof(b)); for(rg int k=1;k<=2;++k) for(rg int i=1;i<=2;++i) for(rg int j=1;j<=2;++j) b[i][j]=(b[i][j]+(a[i][k]*a[k][j])%mod)%mod; memcpy(a,b,sizeof(b)); } inline void matrix_ksm(ll bas){ while(bas){ if(bas&1) matrix(); matrix_(); bas>>=1; } } int main() { scanf("%lld",&n); a[1][1]=a[1][2]=a[2][1]=1; ans[1][1]=ans[2][2]=1; matrix_ksm(n); printf("%lld",ans[2][1]); return 0; }
以上是关于[P1962] 斐波那契数列 (矩阵快速幂)的主要内容,如果未能解决你的问题,请参考以下文章